Square & Square Root of 89 – Examples, Methods, Calculation

Within algebraic mathematics, squares and square roots stand pivotal. Squaring, illustrated by multiplying a number by itself, like 89 to yield 7921, is fundamental. It’s a cornerstone for rational and irrational number exploration. Rational numbers express as fractions of integers, while irrationals defy neat fraction expression. Understanding these basics enriches mathematical comprehension, revealing intricate relationships and patterns.

Square of 89

The square number of 89, a cornerstone in mathematics, yields 7921, showcasing the significance of squaring. Multiplying the number by itself elucidates properties crucial for algebraic exploration, understanding rational and irrational numbers, and comprehending mathematical patterns and relationships.

Square Root of 89

The square root of 89, a fundamental mathematical concept, is 9.43398113206. It signifies the number multiplied by itself to reach 89. Mastery of square roots is crucial for understanding algebraic relationships and delving into number properties, rational and irrational alike. It unveils key mathematical principles and facilitates problem-solving across diverse domains.

Is the Square Root of 89 Rational or Irrational?

The square root of 89 is irrational. Irrational numbers cannot be expressed as a fraction of two integers and their decimal representations neither terminate nor repeat. Thus, √89 cannot be expressed as a simple fraction and its decimal representation goes on infinitely without a repeating pattern.

A rational number is any number expressible as a fraction of two integers.
Examples : 3/4 or -5/2

An irrational number cannot be expressed as a fraction of two integers and its decimal expansion neither terminates nor repeats.
Examples : √2, which is approximately 1.41421356…, is irrational.

Methods to Find Value of Root 89

There are several methods to find the value of the square root of 89:

1. Prime Factorization Method: Express 89 as a product of prime factors (89 is a prime number, so it’s only divisible by 1 and 89), then group the factors into pairs. The square root of 89 is the product of the square roots of these pairs.
2. Estimation Method: Approximate the square root of 89 by finding perfect squares near it. Since 89 is between 81 (9²) and 100 (10²), its square root is between 9 and 10. Refine the estimate using methods like Newton’s method.
3. Long Division Method: Use the long division method to find the square root of 89 iteratively. This involves dividing 89 by a guess, averaging the result with the guess, and repeating until a satisfactory level of precision is achieved.
4. Calculator or Software: Use a calculator or mathematical software to directly compute the square root of 89. Most calculators and software packages have built-in functions for calculating square roots.
5. Continued Fraction Expansion: Express the square root of 89 as a continued fraction and approximate its value by truncating the expansion at a certain point.

Square Root of 89 by Long Division Method

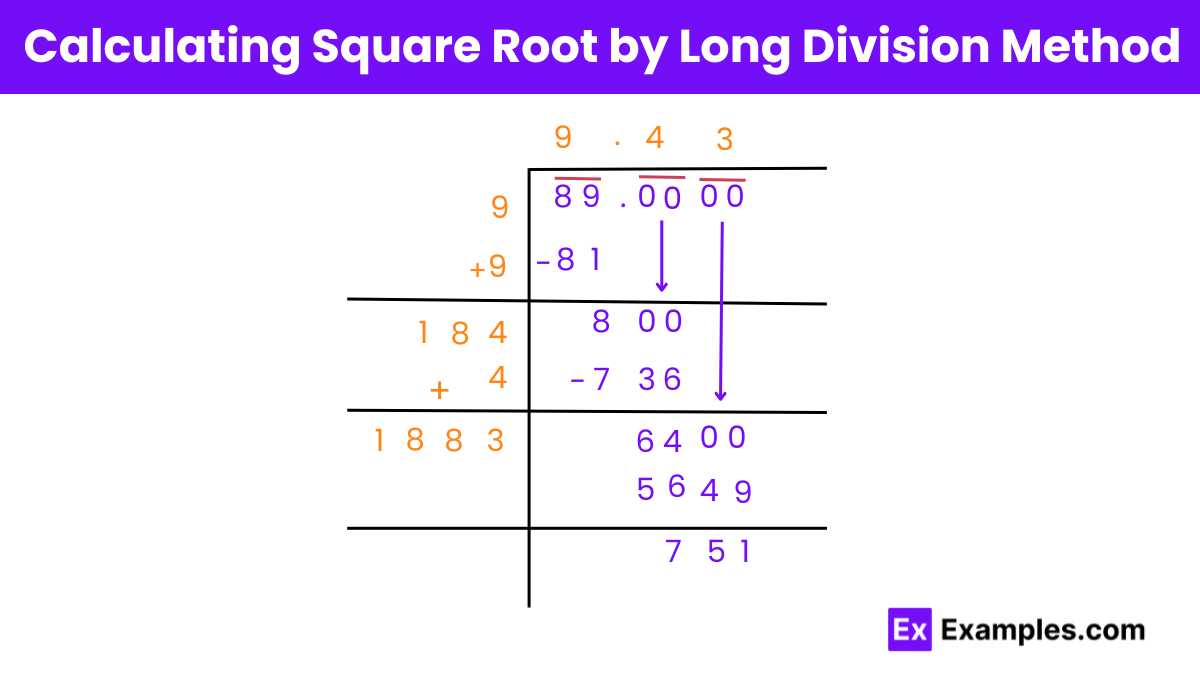
The long division method stands as a common and reliable approach for finding square roots. It simplifies multi-digit numbers into manageable parts, aiding comprehension and accuracy.

To find the square root of 89 using long division:

Step 1: Write 89 within the division symbol.

Step 2: Divide 89 into pairs, resulting in just 89.

Step 3: Start dividing the number, aiming for a quotient that, when squared, is either equal to or less than 89. Here, the quotient is 8 with a remainder of 8.

Step 4: Bring down the next pair, making the dividend 800. Double the previous quotient (8) to get 16, which becomes the next divisor.

Step 5: Pair 16 with another digit to form a divisor that, when multiplied by itself, results in a number close to 800. If necessary, add pairs of zeros to the right before beginning division.

89 is Perfect Square root or Not

No, 89 is not a perfect square. A perfect square is a number that can be expressed as the product of an integer with itself. For example, 9 is a perfect square because it is equal to 3 × 3. However, 89 cannot be expressed as the product of two equal integers, so it is not a perfect square.

FAQs

How can I calculate the square root of 89?

You can calculate the square root of 89 using various methods such as prime factorization, estimation, long division, calculator or software, or continued fraction expansion.

What is the significance of the square and square root of 89?

Understanding the properties and relationships involving the square and square root of 89 is fundamental in mathematics. It helps in exploring algebraic concepts, rational and irrational numbers, and mathematical patterns.

How can I use the square root of 89 in real-life applications?

The square root of 89 can be used in various practical scenarios such as engineering calculations, physics problems, financial modeling, and computer science algorithms.

Is there any interesting mathematical property related to the square root of 89?

One interesting property related to the square root of 89 is that it is an irrational number, meaning its decimal representation goes on infinitely without repeating. This property is shared by all square roots of non-perfect square numbers.