What is the square of 30?
400
600
700
900

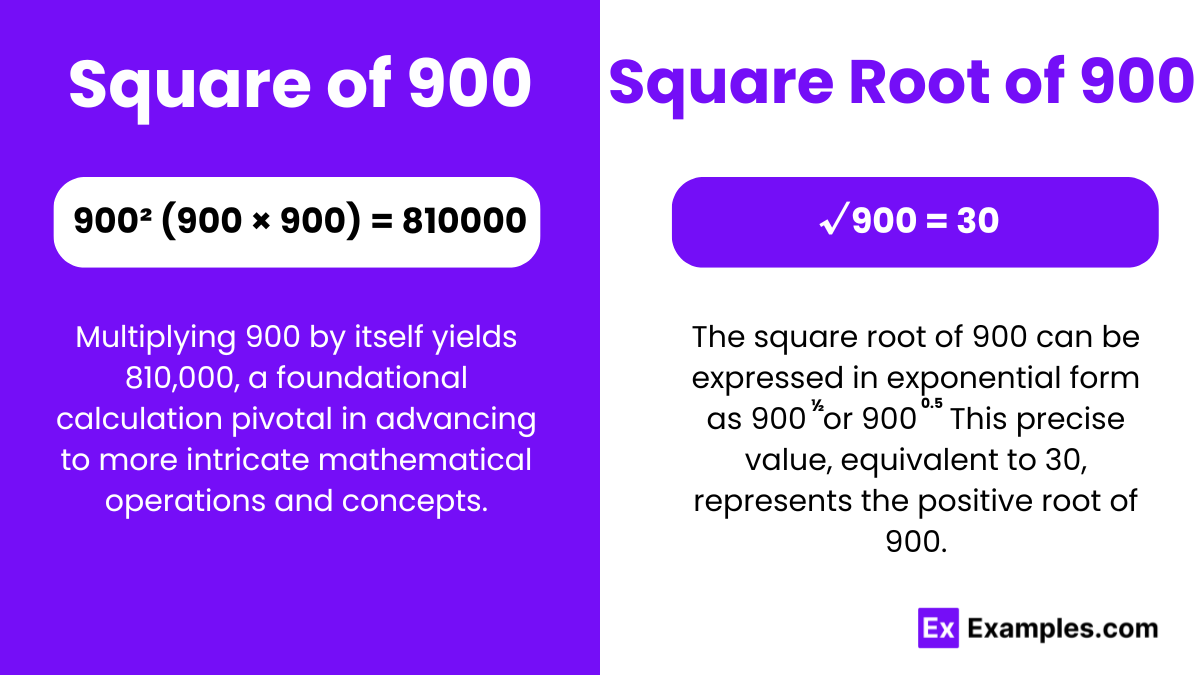
Within algebraic studies, the pivotal concepts of squares and square roots are foundational. Squaring, demonstrated by multiplying a number like 900 by itself to yield 810000, is fundamental. This operation is cornerstone in exploring rational (fractional) and irrational numbers. Understanding these concepts enriches comprehension of mathematical relationships and patterns. In algebraic contexts, squares and square roots are paramount. They elucidate properties of numbers, rational or irrational, and their interplay within equations and expressions. Mastery of these fundamentals enhances mathematical proficiency and insight, facilitating deeper exploration of algebraic concepts and their applications in diverse fields.
A square number, like 900, results from multiplying a number by itself. The square of 900 is 810,000. Understanding square numbers elucidates mathematical patterns and relationships, crucial in algebraic studies. They form a cornerstone in comprehending numerical properties and their significance in various mathematical contexts.
The square root, exemplified by the Square Root of 900, is a fundamental mathematical operation. The Square Root of 900 is 30. Comprehending square roots unveils numerical relationships, pivotal in algebraic investigations. It forms a basis for understanding complex equations and exploring mathematical intricacies across diverse disciplines.
Square Root of 900: 30
Exponential Form: 900^½ or 900^0.5
Radical Form: √900
The square root of 900 is rational. This is because 900 is a perfect square, being the product of a whole number (30) multiplied by itself. In general, the square root of any perfect square is a rational number.
A rational numbers is any number that can be expressed as a fraction of two integers, where the denominator is not zero. Since 18 can be expressed as 18/1, it fits this definition, making it a rational number.
Rational numbers are numbers that can be expressed as a quotient or fractions of two integers, where the denominator isn’t zero.
Examples : 1/2, 3/4, −5/7
Irrational numbers cannot be expressed as fractions and have non-repeating, non-terminating decimals.
Examples : π, √2, and e.
There are several methods to find the value of the square root of 900:
Calculator: The easiest and most common method is to use a calculator. Simply input “√900” into a calculator, and it will give you the answer directly, which is 30.
Prime Factorization: You can break down 900 into its prime factors, which are (2², 3², 5²). Then, take one factor from each pair and multiply them together, giving you (2 \times 3 \times 5 = 30).
Long Division: This method involves dividing 900 by a number repeatedly until you get a quotient close to the divisor. This process requires some trial and error, but it’s a good exercise for understanding square roots. Start with a guess (e.g., 30), divide 900 by this guess, adjust your guess as needed, and continue until you find the square root.
Estimation: Since 900 is very close to the perfect square 961 (31²) you can estimate the square root to be close to 31. This gives you a ballpark figure to work with.
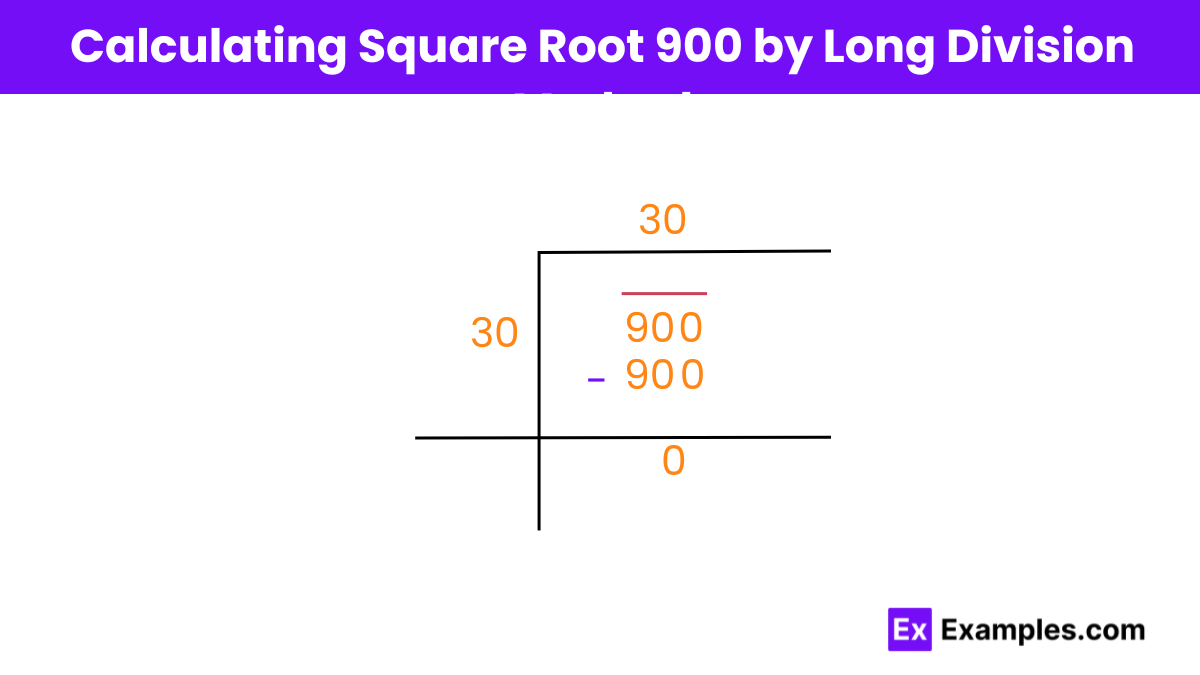
Finding the Square Root of 900:
First, we look for a number that, when multiplied by itself, equals a number that’s less than or equal to 900. This gives us a starting point to work with.
Long Division for Square Root:
We perform long division to find the square root of 900. We divide 900 by numbers starting from 1 until we find one that gives a quotient with no remainder.
Completion of Long Division:
When we find a number that evenly divides 900 without leaving a remainder, like 30, we stop the long division process. Since the remainder is 0, we’ve found our square root.
Considering Negative Square Root:
Now, can the square root of 900 be -30? We can find out by squaring -30. (-30²) equals 900, confirming that -30 is indeed a valid square root of 900. However, typically, we consider only the positive root unless specified otherwise.
Real or Imaginary Number:
Lastly, what about (√-900)? Well, in the realm of real numbers, there’s no number whose square is negative. So, (√-900) is not a real number. It belongs to the domain of complex numbers.
Yes, 900 is a perfect square because it is the square of a whole number. Specifically, (30² = 900), indicating that 900 is a perfect square.
Yes, because (−30)2=900(−30)2=900. However, the convention is to consider only the positive square root unless specified otherwise.
No, because in the realm of real numbers, there’s no number whose square is negative. The square root of -900 belongs to the domain of complex numbers.
You can calculate it using methods like prime factorization, long division, or simply by using a calculator.
A square number is the result of multiplying a number by itself. In the case of 900, it is a square number because 30×30=900
Understanding square roots is crucial in various fields such as engineering, physics, and finance. For example, in engineering, it’s used in calculating areas, volumes, and dimensions. In finance, it’s used in calculating interest rates and investment growth.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the square of 30?
400
600
700
900
Find the square root of 900.
30
20
15
10
What is the result of squaring the square root of 900?
900
30
60
1000
If x² = 900, what is the approximate value of x?
30
35
40
45
What is the result of 900 divided by its square root?
30
25
15
10
What is the square root of 3600 divided by 2?
30
45
60
90
Find the number whose square root is 30.
700
800
900
1000
What is the square of the result obtained by adding the square root of 900 to 10?
1600
900
1400
1200
What is the difference between 900 and the square of its square root?
100
300
600
0
What is the product of the square root of 900 and 5?
150
250
350
450
Before you leave, take our quick quiz to enhance your learning!

