Square & Square Root of 97 – Examples, Methods, Calculation

Within the realm of mathematics, particularly in algebraic studies, the foundational concepts of squares and square roots are pivotal. The process of squaring a number, such as 97, entails multiplying it by itself to yield 9409, underscoring a fundamental operation. This operation serves as a cornerstone in probing the properties inherent in both rational numbers, expressible as fractions, and irrational numbers, defying neat fractional expressions. Understanding these fundamental concepts enriches one’s comprehension of mathematical relationships and patterns, essential in exploring the intricacies of numerical systems. These concepts are integral to various mathematical disciplines, fostering a deeper insight into the interconnectedness and significance of algebraic principles in mathematical discourse.

Square of 97

A square number, like 576, is the result of multiplying an integer by itself. Its square root is 24, the number that, when multiplied by itself, equals 576. In contrast, the square root of 97 is an irrational number, approximately 9.85, requiring methods like prime factorization for calculation.

Square Root of 97

“The square root of 576, a perfect square, is 24, as 24 multiplied by itself equals 576. Conversely, the square root of 97 is an irrational number, approximately 9.85. Understanding square roots unveils the relationship between numbers and their squares, integral to mathematical exploration and problem-solving.”

Is the Square Root of 97 Rational or Irrational?

The square root of 97 is an irrational number. It cannot be expressed as a fraction of two integers. Approximated to about 9.85, it signifies a non-repeating, non-terminating decimal. This characteristic distinguishes it from rational numbers, illustrating the diverse nature of mathematical expressions.

Rational number : Rational number is one that can be expressed as a fraction of two integers, such as 3/4 or -5/2. These numbers possess finite or repeating decimal representations.

Irrational number : Irrational number cannot be expressed as a fraction of two integers, and its decimal expansion neither terminates nor repeats. For instance, the square root of 2 (√2) is approximately 1.41421356…, exemplifying irrationality. These numbers unveil a distinct property in mathematics due to their non-repeating, non-terminating nature, challenging conventional numerical representations.

Methods to Find Value of Root 97

Several methods can be employed to find the value of the square root of 97:

1. Prime Factorization: Express 97 as a product of prime numbers and extract the square root.
2. Newton’s Method: Iteratively refine an initial guess to approximate the square root.
3. Binomial Expansion: Use binomial expansion to approximate the square root.
4. Continued Fractions: Express the square root as a continued fraction and approximate its value.

Each method offers its own advantages and may be chosen based on computational ease and accuracy requirements.

Square Root of 97 by Long Division Method

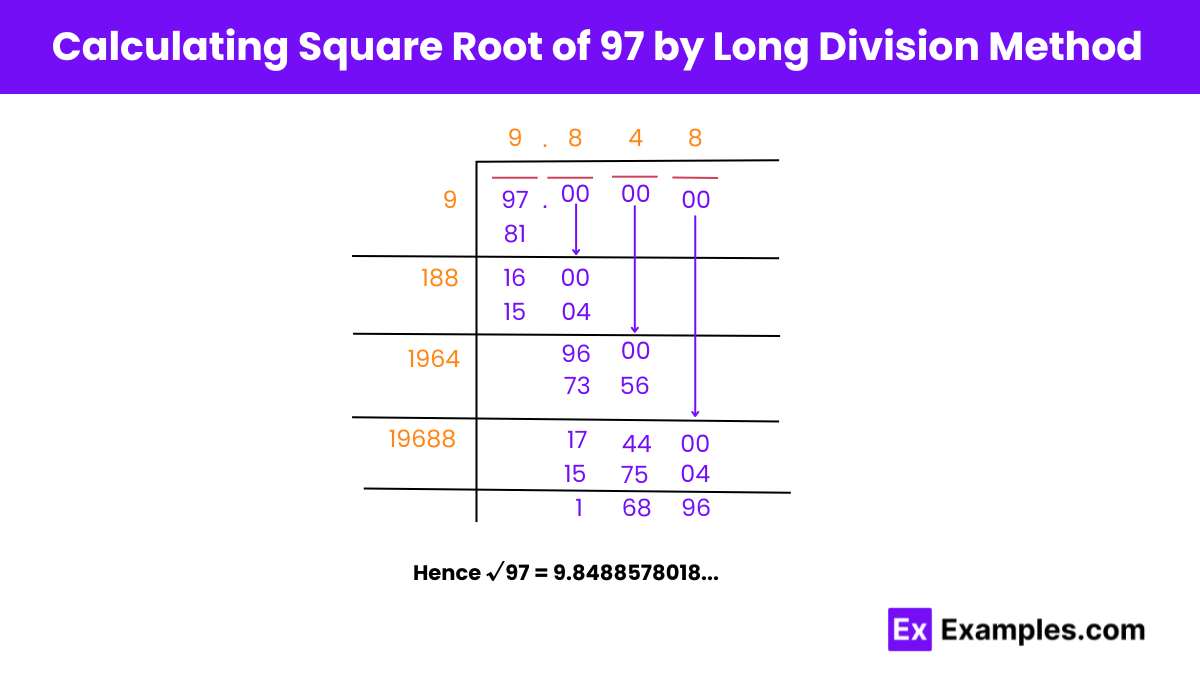
Finding Square Root of 97 Using Long Division

Step 1: Pairing Digits
Start by pairing the digits of the given number, starting with the digit at the one’s place, and indicate the pairing with a horizontal bar.

Step 2: Initial Divisor
Find a number that, when squared, gives a product less than or equal to 97. Since 9 × 9 = 81 ≤ 97, the initial divisor is 9, and the quotient is also 9. Proceed with the division.

Step 3: Updating Divisor
Bring down the next pair of digits (00) and multiply the quotient by 2 to get 18, which becomes the starting digits of the new divisor.

Step 4: Division
Determine the next digit of the quotient by finding the largest digit that, when appended to the current quotient, produces a product less than or equal to the current partial dividend. Proceed with the division to get the remainder.

Step 5-8: Repeat the Process
Continue bringing down pairs of digits and updating the divisor until the desired level of precision is reached or until a satisfactory approximation of the square root of 97 is obtained. Repeat the division process until the remainder is negligible or within an acceptable margin of error.

97 is Perfect Square root or Not

97 is not a perfect square; it lacks integer factors. Therefore, its square root is irrational. Approximated to about 9.85, it denotes a non-repeating, non-terminating decimal. The absence of integer factors distinguishes it from perfect squares, showcasing the diverse nature of mathematical expressions.

FAQs

Can the square root of 97 be expressed as a fraction?

No, the square root of 97 cannot be expressed as a fraction of two integers since it is an irrational number.

Is the square root of 97 a terminating or repeating decimal?

No, the square root of 97 is neither terminating nor repeating; it is a non-repeating, non-terminating decimal.

How many decimal places should I use to approximate the square root of 97?

It depends on your level of precision. Typically, approximating to several decimal places like 9.8488578 is sufficient for most calculations.

Can the square root of 97 be simplified by using radicals?

No, the square root of 97 cannot be simplified further using radicals since it is an irrational number.

What practical applications involve the square root of 97?

The square root of 97 may be used in various fields such as mathematics, physics, engineering, and finance for calculations involving areas, distances, and measurements.

How does the square root of 97 compare to other square roots?

Compared to perfect square roots, like √100 = 10, the square root of 97 is irrational and lies between the perfect squares of 9 and 10.