Law of Universal Gravitation – Examples, Definition, Formula, Functions

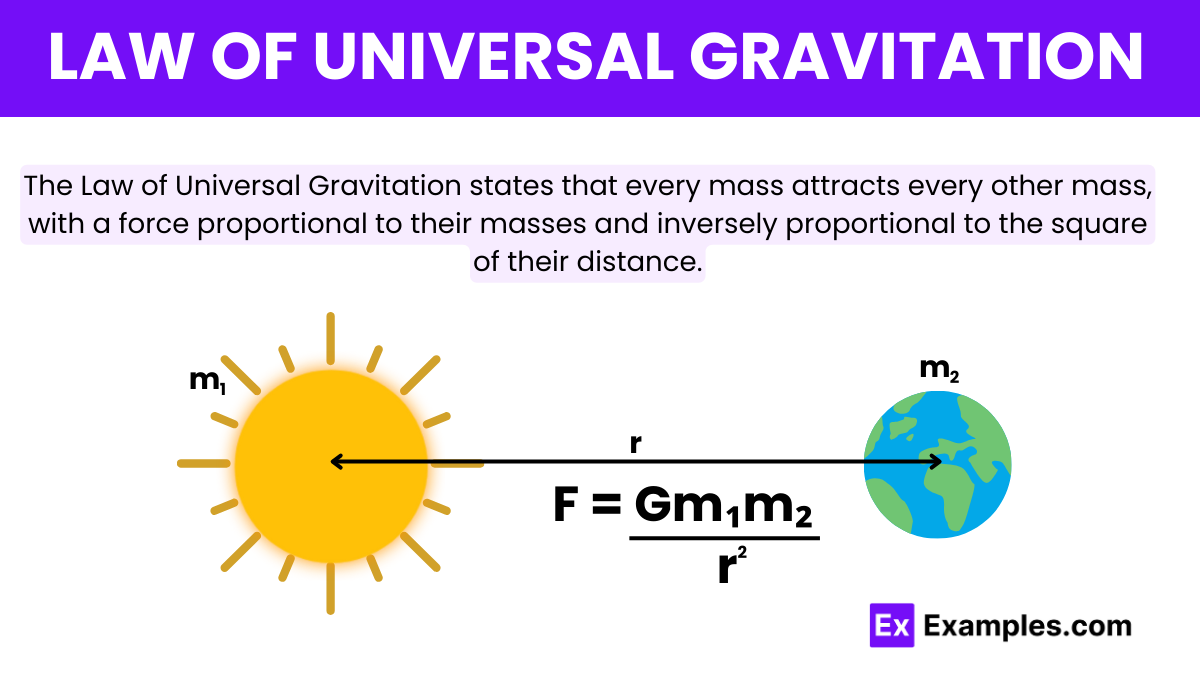
The Law of Universal Gravitation is a vital principle in physics, especially within the laws of mechanics. It tells us that every object in the universe pulls on every other object with a force. This force depends on two things: the masses of the objects and the distance between them. Specifically, the force increases as the masses increase and decreases as the distance between the objects grows. Discovered by Sir Isaac Newton, this law is essential for understanding many of the laws of physics, including why planets orbit the sun and why objects fall to the ground on Earth. It’s a foundational concept that helps us understand the forces at work in the universe.

What is Law of Universal Gravitation?

Law of Universal Gravitation Formula

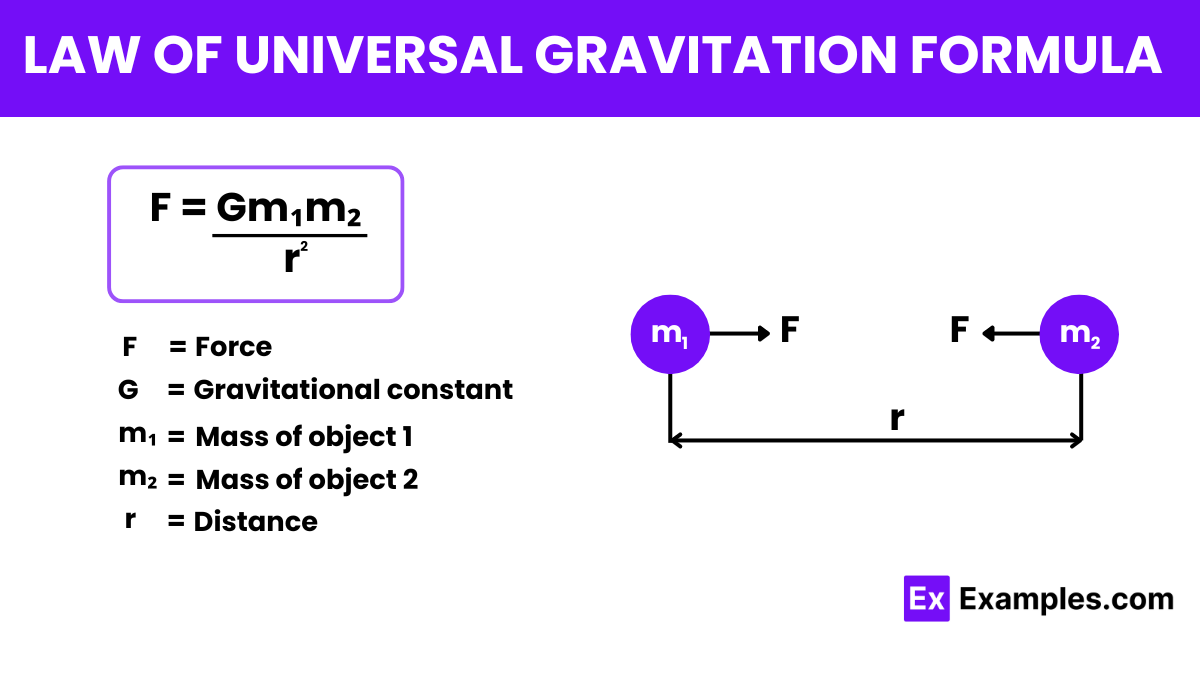
The formula for the Law of Universal Gravitation is​​

• 𝐹 represents the gravitational force between two objects.
• m₁​ and m₂ are the masses of the objects.
• r is the distance between the centers of the two objects.
• G is the gravitational constant, a number that helps calculate the strength of the gravitational force.

Vector form

Here’s what each symbol represents:

• F is the vector representing the gravitational force exerted between two objects.
• G is the gravitational constant, which is a fixed value used to calculate gravitational forces.
• m₁ and m₂ are the masses of the two objects involved.
• r is the distance between the centers of the two masses.
• r̂ is the unit vector pointing from one mass to the other, indicating the direction of the force.

In this formula, the force is described as being attractive (pulling the two masses together), and the direction of the force is always along the line connecting the centers of the two masses. This means if m₁​ is considering the force it experiences due to m₂, then r̂ points from m₁​ towards m₂​, and vice versa, ensuring that the force is always attractive, pulling the two objects together. This vector form is crucial for accurately describing the dynamics of celestial bodies and any system where gravitational interactions are significant.

Gravity field

The gravitational field (𝑔⃗) of an object is defined as the gravitational force per unit mass exerted at a point in space due to the presence of the mass. It provides a way to describe how strong the gravitational pull is at different points around the object, without needing to consider the specific properties of a second object being acted upon.

Mathematical Expression:

Where:

• g​ is the gravitational field vector at a point in space.
• G is the gravitational constant.
• 𝑀 is the mass of the object creating the gravitational field.
• 𝑟 is the distance from the center of the mass 𝑀 to the point where the field is being calculated.
• r̂ is the unit vector pointing from the mass 𝑀 towards the point of interest.

In this formula, the negative sign indicates that the field vector points towards the mass M creating the field, reflecting the attractive nature of gravity. This field is what causes other masses that enter into the space around M to experience a gravitational force. The strength of the gravitational field decreases with the square of the distance from the mass, meaning it weakens as you move further away from the source mass.

Steps to Calculate Gravitational Force

1. Identify the Masses: Determine the masses of the two objects involved. For example, if calculating the force between the Earth and an apple, use the mass of the Earth and the mass of the apple.
2. Measure the Distance: Measure the distance between the centers of the two objects. In many cases involving an object on Earth, this would be the distance from the center of the Earth to the object at the surface.
3. Apply the Formula: Plug the values into the formula. Multiply the masses, divide by the square of the distance, and multiply by the gravitational constant G.

Universal Gravitational Constant

The Universal Gravitational Constant, often represented by the symbol G, is a key number we use to calculate the gravitational force between two objects. This constant helps us figure out exactly how strong the pull of gravity is. Imagine you want to find out how much force is pulling between two planets or between a planet and a star. To do this, you multiply their masses and then divide by the square of the distance between them. After that, you multiply the result by G to get the force of gravity.

In numbers, the value of G is approximately

cubic meters per kilogram per second squared (m³ /kg/ s²). This might sound really small, but it’s the perfect amount to calculate the vast forces acting over the huge distances in space. Using G, we can predict how planets will orbit the sun, how moons orbit their planets, and even how astronauts need to move in space to go from one place to another. It’s like a universal rule that all objects in the universe follow when it comes to gravity.

Law of Universal Gravitation Functions

1. Calculating Gravitational Force: It allows us to compute the force of attraction between any two objects with mass. This helps scientists and engineers determine how planets, stars, and other celestial bodies move and interact.
2. Understanding Orbital Motion: This law explains why planets orbit around the sun and why moons orbit planets. The gravitational pull keeps these bodies in a predictable path around their larger counterparts.
3. Tides Prediction: The gravitational forces between the Earth and the Moon cause the ocean tides. By understanding this law, we can predict high and low tides, which is crucial for navigation and coastal management.
4. Space Exploration: Engineers use this law to design spacecraft trajectories, ensuring they enter orbits correctly and reach their destinations, such as other planets or moons.

Law of Universal Gravitation Examples

1. Falling Objects: When you drop a ball, it falls to the ground due to the gravitational pull between the Earth and the ball. The Earth’s mass attracts the ball, pulling it downward.
2. Orbiting Planets: The Earth orbits the Sun because of the gravitational force between them. The Sun’s massive size creates a strong pull that keeps the Earth traveling in a circular path around it.
3. Moon’s Orbit: Just as the Earth orbits the Sun, the Moon orbits the Earth. The gravitational attraction between the Earth and the Moon keeps the Moon in its path around our planet.
4. Tides: The high and low tides in the oceans are caused by the gravitational pull of the Moon. The Moon’s gravity pulls on the Earth’s water, causing it to bulge out in the direction of the Moon.
5. Spacecraft Maneuvers: When astronauts need to adjust the orbit of a spacecraft, they rely on the gravitational forces between the spacecraft and the Earth or other celestial bodies. By calculating these forces, they can determine the best way to use thrusters to change the spacecraft’s path.
6. Vehicle Stability: Cars and bikes remain on the ground and do not float away due to gravity.
7. Gravitational Slingshot: Space probes often use a technique called a gravitational slingshot to gain speed and change direction. They pass close to a planet, using its gravitational force to boost their velocity without using extra fuel.
8. Apples Falling from Trees: A classic example inspired by Sir Isaac Newton himself is an apple falling from a tree. The Earth’s gravitational pull causes the apple to accelerate towards the ground once it detaches from the tree.
9. Black Holes: These are regions of space where gravitational pull is so strong that nothing, not even light, can escape.

Limitations

1. Does Not Apply at Very Small Scales: Newton’s law does not accurately describe gravitational interactions at the atomic or subatomic levels. Quantum mechanics is required to explain the forces and behaviors in these domains.
2. Cannot Explain Mercury’s Orbit: The Law of Universal Gravitation cannot fully account for the precession of Mercury’s orbit. Albert Einstein’s General Theory of Relativity provided corrections that more accurately describe the orbit, particularly near massive bodies like the sun.
3. Assumes Instantaneous Action at a Distance: Newton’s formulation implies that gravitational effects propagate instantaneously. However, according to relativity theory, changes in the gravitational field propagate at the speed of light, not instantaneously.
4. Ignores Relativistic Effects: For objects moving at speeds close to the speed of light or in very strong gravitational fields, Newtonian gravity is not sufficient. Relativistic effects, as described by Einstein’s theory, become significant and must be considered.
5. Simplifies Objects as Point Masses: The law simplifies objects to point masses, which is not always practical. Real objects have distributions of mass and complex shapes that can affect gravitational interactions, particularly at close distances.
6. Difficulty with Large-Scale Predictions: Newton’s law faces challenges when applied to very large scales, such as in predicting the behavior of galaxies or the overall dynamics of the cosmos, where dark matter and dark energy play significant roles.

FAQs

Is Universal Gravitation a Law or Theory?

Universal Gravitation is a law that mathematically describes the gravitational force but does not explain the underlying cause.

Is Universal Law of Gravitation Wrong?

The Universal Law of Gravitation is not wrong but limited. It does not explain certain phenomena like the orbit of Mercury, which General Relativity does.

Why is the Law of Gravity Not a Theory?

Laws describe what happens; theories explain why. The Law of Gravity describes gravitational forces but does not explain their underlying nature.