Darcy’s Law – Examples, Definition, Formula, Limitations, FAQ’S

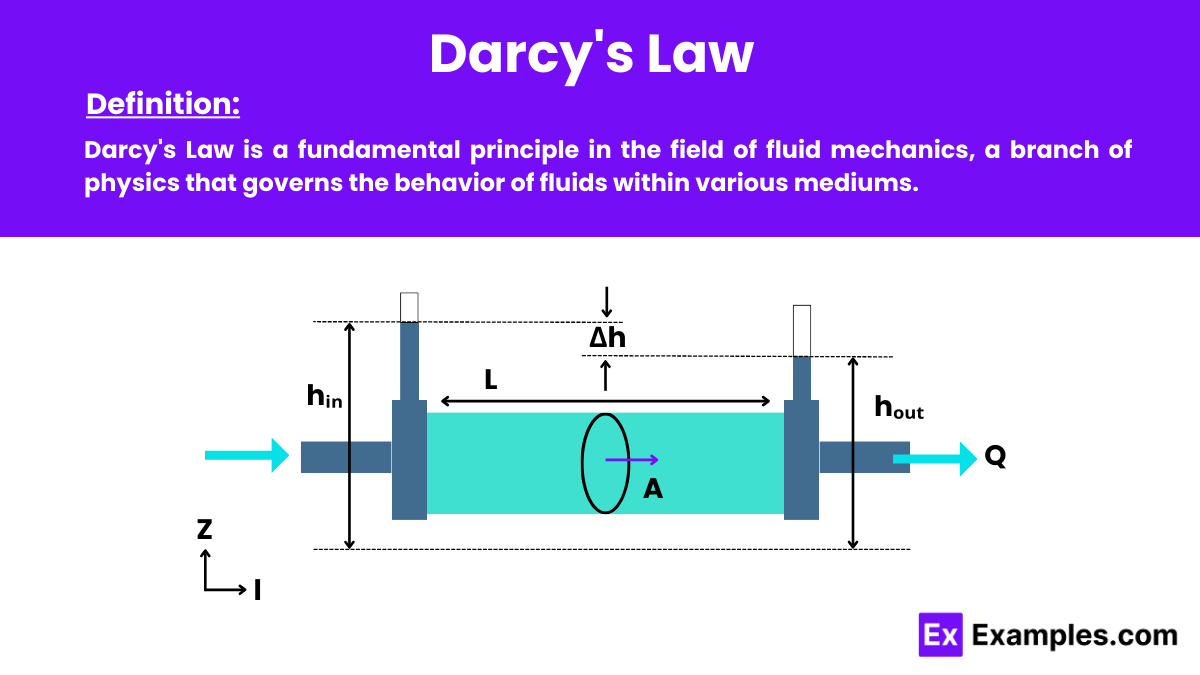
Darcy’s Law is a fundamental principle in the field of fluid mechanics, a branch of physics that governs the behavior of fluids within various mediums. This law of physics quantitatively describes the flow of a fluid through a porous medium. Specifically, This Law states that the flow rate of the fluid through the porous medium is proportional to the pressure difference across the medium and inversely proportional to the resistance to flow, which is affected by the properties of the medium and the fluid. This law is vital for understanding and predicting the movement of water and other fluids in natural and engineered systems.

What is Darcy’s Law?

Darcy’s Law Formula

Darcy’s Law is mathematically expressed by the formula:

Where:

• 𝑄 is the rate of water flow,
• 𝐾 is the hydraulic conductivity,
• 𝐴 is the column cross-section area, and
• 𝑑ℎ/𝑑𝑙​ indicates a hydraulic gradient.

This equation is commonly used in hydrology and fluid mechanics to calculate the flow of water through porous media, such as soil or rock. The negative sign indicates that water flows from higher hydraulic head (or elevation) to lower hydraulic head, following the direction of decreasing hydraulic gradient.

This formula indicates that the flow rate is directly proportional to the permeability of the medium and the pressure difference. And inversely proportional to the length of the medium through which the fluid is flowing.

Limitations of Darcy’s Law

1. Turbulent Flow Discrepancies: Darcy’s Law assumes laminar flow, but it fails to predict flow rates accurately when flow becomes turbulent, typically at higher velocities or in media with larger pores.
2. Compressibility Issues: The law applies best to incompressible fluids. For compressible fluids like gases, pressure changes significantly affect density and flow dynamics, thus requiring modifications to the law.
3. Variability in Medium: The assumption that the porous medium is homogeneous and isotropic limits Darcy’s Law. In real-world applications. Variations in permeability due to heterogeneous or anisotropic conditions can cause inaccuracies.
4. Reynolds Number Constraints: Darcy’s Law is effective only at low Reynolds numbers, where flow remains laminar. At higher values, the linear relationship between flow rate and pressure gradient breaks down.
5. Alterations by Chemical and Biological Factors: If chemical reactions or biological growth alter the fluid or medium properties, such as through biofilm development, these changes can affect permeability and porosity, impacting flow predictions.
6. Temperature Effects: Changes in temperature can alter the fluid’s viscosity and the medium’s structural properties, which Darcy’s Law does not account for. Affecting the accuracy of flow predictions under varying thermal conditions.

Uses of Darcy’s Law

1. Groundwater Management: Hydrogeologists use Darcy’s Law to calculate groundwater flow rates. Which is essential for managing water resources and assessing aquifer sustainability.
2. Oil Recovery: In the petroleum industry, engineers apply Darcy’s Law to optimize oil recovery techniques by understanding how oil flows through porous rock formations.
3. Environmental Engineering: Environmental engineers use Darcy’s Law to design and assess the effectiveness of remediation systems that remove contaminants from soil and water.
4. Civil Engineering: Darcy’s Law helps civil engineers in designing efficient drainage systems and evaluating soil stability in projects such as landfills and earth dams.
5. Agriculture: Agronomists apply Darcy’s Law to understand soil water movement, which assists in making informed decisions about irrigation practices and crop rotation strategies.
6. Filter Design: Engineers use Darcy’s Law to design filters and determine the flow of fluids through filter materials, essential for ensure the effectiveness of water purification systems.

Examples for Darcy’s Law

1. Groundwater Flow in Aquifers:
   Scientists use Darcy’s Law to measure water flow in aquifers. This guess helps them predict how water will travel through soil and rock layers, particularly for managing water resources and assessing the spread of contaminant.
2. Oil and Gas Reservoirs:
   Engineers apply Darcy’s Law to determine the permeability of rock formations in oil and gas exploration. This calculation helps identify productive reservoir and estimate extract resources. Allowing for optimal drill.
3. Soil Remediation:
   Darcy’s Law aids in checking how remediation fluids permeate contaminated soil. This estimation ensures that chemicals will disperse effectively, leading to thorough decontamination.
4. Artificial Recharge of Aquifers:
   Hydrologists use Darcy’s Law to measure the rate at which surface water seeps down to recharge groundwater aquifers artificial. This application ensures efficient water replenishment.
5. Riverbank Filtration:
   Water engineers apply Darcy’s Law to predict the flow and quality of river water passing through riverbanks into aquifer. This information helps design optimal extraction systems for potable water.

FAQ’S

What is the Darcy law of hydrology?

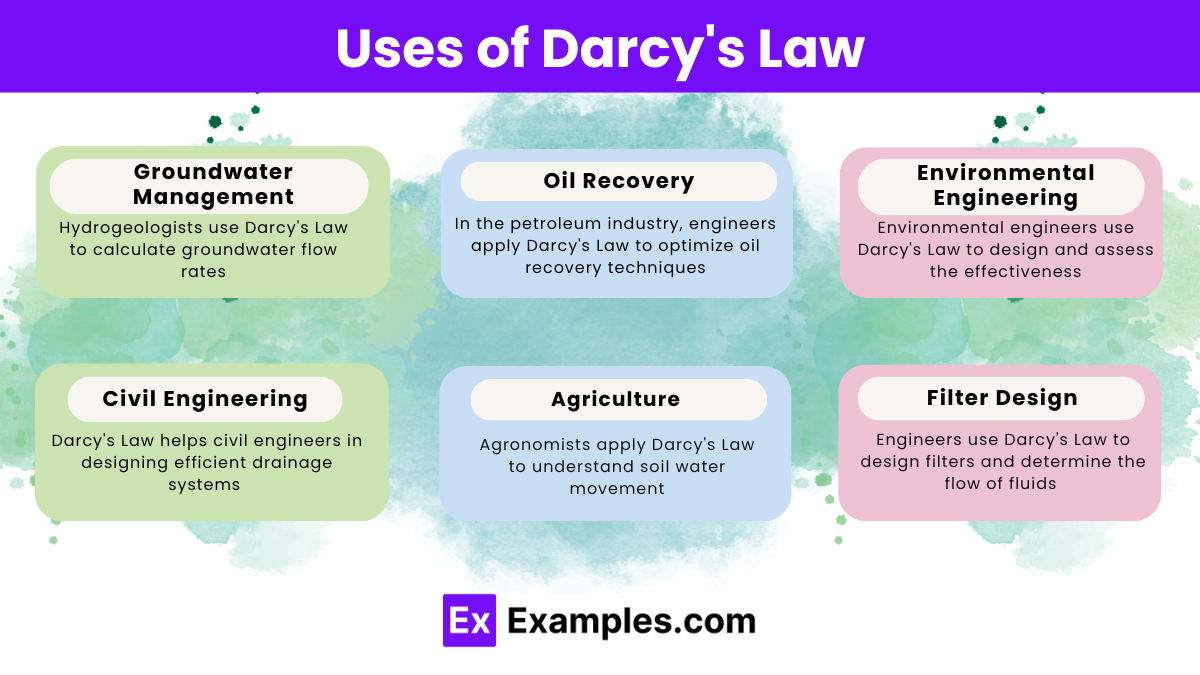
Darcy’s Law defines the relationship between fluid flow through porous media and the driving hydraulic gradient. Specifically, it predicts the flow rate using hydraulic conductivity and cross-sectional area.

Is Darcy’s law valid?

Yes, Darcy’s Law is valid under conditions where the flow remains laminar. However, it may lose accuracy with high flow rates and turbulent conditions, where deviations from the law occur.

What is the Reynolds number for Darcy’s law?

The Reynolds number for Darcy’s Law, indicating laminar flow through porous media, is generally less than one. This low value ensures that the flow remains steady and predictable.