What does the Law of Conservation of Angular Momentum state?
Angular momentum changes with time
Angular momentum is conserved in the absence of external torques
Angular momentum is always constant
Angular momentum increases with external force

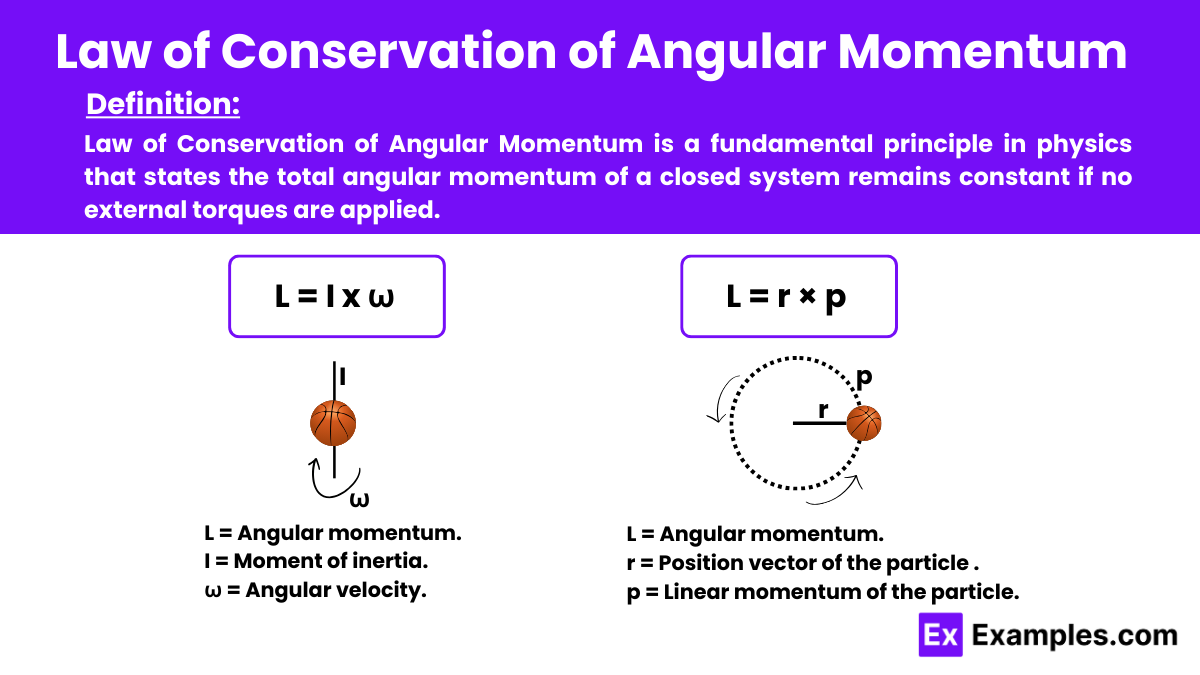
Law of Conservation of Angular Momentum is a fundamental principle in physics that states the total angular momentum of a closed system remains constant if no external torques are applied. This law of physics reflects the rotational analog of linear momentum conservation, emphasizing that angular momentum is conserved in systems where net external torque is zero. This principle is crucial for analyzing the rotational motion of various systems, from simple mechanical setups to complex celestial interactions.
The Law of Conservation of Angular Momentum states that the total angular momentum of a system remains constant if no external torques act on it. This principle, a cornerstone in physics, particularly mechanics, applies to many phenomena, from the motion of orbiting celestial bodies to the behavior of spinning objects and moving particles. The law implies that in a closed system, where no external forces alter rotational motion, the system retains its initial angular momentum at any point in time.
The Law of Conservation of Angular Momentum is mathematically represented by the formula:
where:
In a closed or isolated system where no external torques apply, the system keeps its total angular momentum constant. Thus, if the system starts with a specific angular momentum, it retains that angular momentum throughout the motion unless an external torque acts upon it. We can express this conservation as:
This principle is crucial for understanding rotational dynamics in various physical contexts, from spinning objects to orbital mechanics in astronomy.
The relationship between torque and angular momentum is a fundamental concept in rotational dynamics. The key relationship is expressed by the following equation:
where:
This equation means that the torque applied to a system is equal to the rate of change of its angular momentum. In simpler terms, any change in the angular momentum of a system is directly caused by and is proportional to the net external torque acting on it. When the net external torque is zero, angular momentum is conserved, and 𝑑𝐿⃗/𝑑𝑡=0, indicating no change in angular momentum.
This relationship is essential for analyzing scenarios where forces are applied off-center to rotating objects. Such as in wheels, spinning tops, planets in orbit, or any system undergoing rotational motion. The direction of the torque vector also determines the direction in which the angular momentum changes. According to the right-hand rule: if you curl the fingers of your right hand in the direction of rotation caused by the torque, your thumb points in the direction of the angular momentum vector.
Angular momentum represents an object’s rotational momentum, calculated as the product of its moment of inertia and angular velocity. It describes the quantity of rotation an object has.
Yes, momentum is always conserved in a closed system. The total momentum remains constant if no external forces act on the system, according to the law of conservation of momentum.
Momentum is a vector. It has both magnitude and direction. With the direction of the momentum vector corresponding to the direction of the object’s velocity.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What does the Law of Conservation of Angular Momentum state?
Angular momentum changes with time
Angular momentum is conserved in the absence of external torques
Angular momentum is always constant
Angular momentum increases with external force
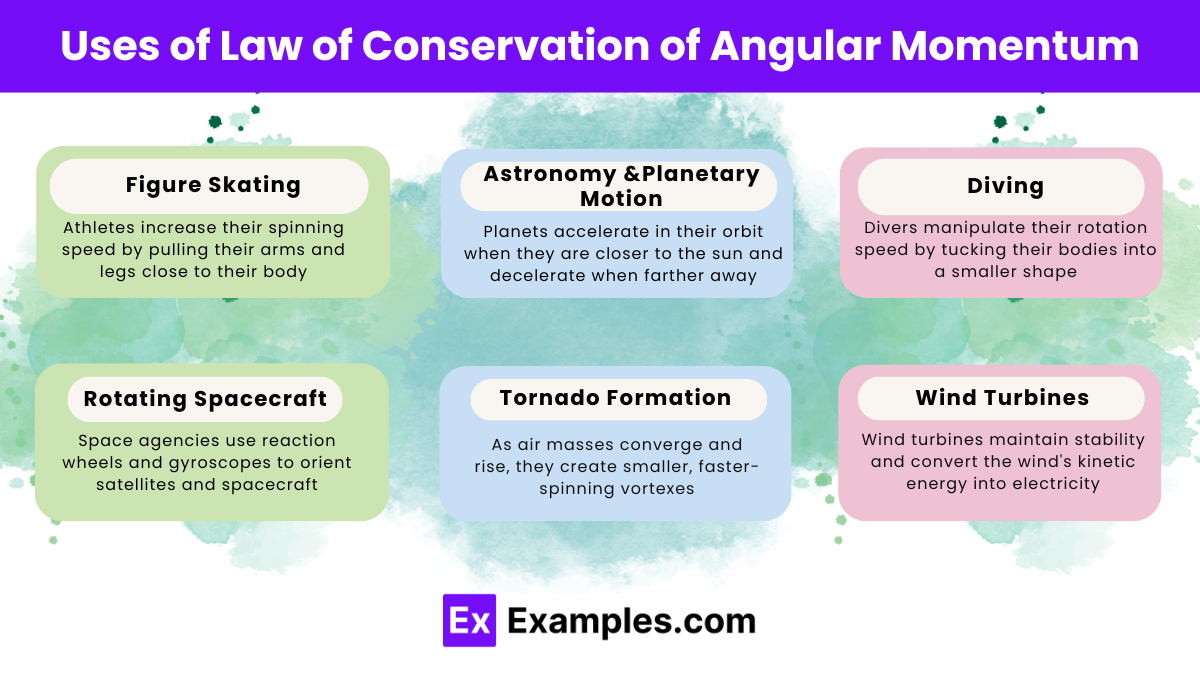
If a figure skater pulls in her arms during a spin, what happens to her angular velocity?
It decreases
It increases
It remains the same
It becomes zero
What happens to the moment of inertia when a diver pulls their legs in during a somersault?
It decreases
It increases
It remains the same
It becomes zero
A rotating disk has an angular momentum L. If the radius of the disk is halved while keeping the mass constant, what happens to the angular velocity?
It is halved
It is doubled
It is quadrupled
It remains the same
In a closed system, if the moment of inertia of a rotating body is increased, what must happen to the angular velocity to conserve angular momentum?
It increases
It decreases
It remains the same
It becomes zero
What is the relationship between torque and angular momentum?
Torque is the rate of change of angular momentum
Torque is the product of angular momentum and angular velocity
Torque is independent of angular momentum
Torque is the sum of angular momentum and force
How does an ice skater increase their spin speed during a performance?
By extending their arms and legs
By pulling in their arms and legs
By jumping higher
By reducing their mass
What quantity remains constant in the absence of an external torque?
Linear momentum
Angular velocity
Angular momentum
Moment of inertia
A planet orbits the sun. If the distance to the sun decreases, what happens to its orbital speed?
It decreases
It increases
It remains the same
It becomes zero
When a gymnast tucks in during a flip, what happens to her angular momentum?
It increases
It decreases
It remains the same
It becomes zero
Before you leave, take our quick quiz to enhance your learning!

