If a coil of 200 turns is rotated in a magnetic field of 0.5 T at a frequency of 60 Hz, what is the peak induced voltage?
18.85 V
37.7 V
75.4 V
150.8 V
of 10
Induced Voltage Formula – Formula, Applications, Limitations, Example Problems
Induced Voltage Formula – Formula, Applications, Limitations, Example Problems
What is Induced Voltage Formula?
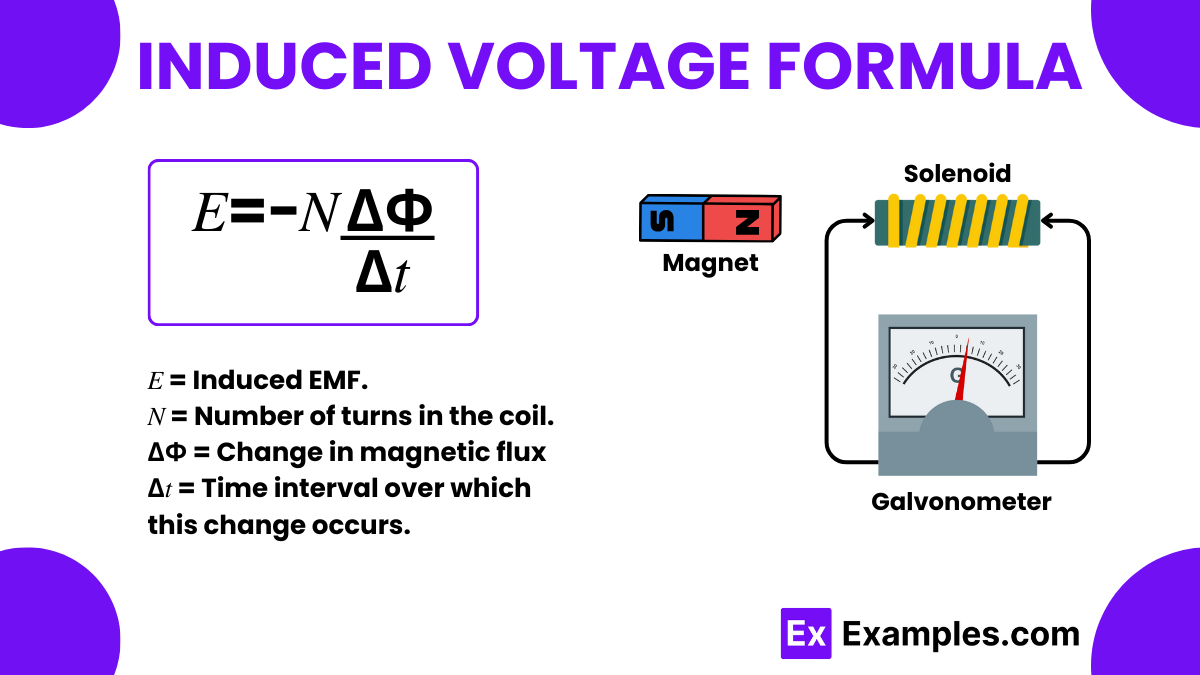
The induced voltage formula, central to electromagnetic induction, was discovered by Michael Faraday, a pioneering figure in electromagnetism. Faraday’s Law of Electromagnetic Induction states that the induced electromotive force (EMF) in any closed circuit equals the rate of change of the magnetic flux through the circuit. This discovery laid the foundation for many of the electrical technologies we use today.
Induced voltage refers to the voltage generated across a conductor when it moves through a magnetic field or when a magnetic field changes around it. The formula to calculate this induced voltage is
- 𝐸 represents the induced EMF.
- 𝑁 is the number of turns in the coil.
- ΔΦ denotes the change in magnetic flux
- Δ𝑡 indicates the time interval over which this change occurs.
This relationship highlights that the induced voltage is proportional to the rate at which the magnetic flux changes with time.
Applications of Induced Voltage Formula
- Electric Generators: Engineers use the induced voltage formula to design electric generators that convert mechanical energy into electrical energy by rotating coils within magnetic fields.
- Transformers: This formula helps in designing transformers, which adjust voltage levels between circuits in power systems, ensuring efficient power distribution.
- Induction Motors: The formula guides the creation of induction motors. This used in various appliances and industrial machinery, utilizing electromagnetic induction to convert electrical energy to mechanical movement.
- Wireless Charging: It aids in developing wireless charging systems that transfer power through electromagnetic fields, allowing devices to charge without direct electrical connections.
- Magnetic Sensors: The induced voltage formula is critical in designing magnetic sensors that detect changes in magnetic fields, widely used in navigation systems and industrial applications.
Limitations of Induced Voltage Formula
- Non-Uniform Magnetic Fields: The formula assumes uniform magnetic fields. It becomes less accurate in non-uniform fields where the magnetic flux varies across different parts of the coil.
- Quasi-static Assumption: It primarily applies under quasi-static conditions; rapid changes or dynamic interactions may not be accurately predicted.
- Ideal Conditions: The formula does not account for practical losses like resistance in the wire and air gaps in magnetic circuits, which can affect performance.
- Simple Configurations: It best applies to simple geometrical configurations; complex shapes require advanced computational methods for precise calculations.
- Excludes Eddy Currents: The formula does not consider eddy currents that can significantly impact induced voltages in conductive materials near changing magnetic fields.
Example Problems on Induced Voltage Formula
Example 1: Calculating Induced EMF in a Solenoid
Problem: A solenoid with 200 turns is placed in a magnetic field. The magnetic flux through the solenoid changes from 0.05 Weber to 0.25 Weber within 0.2 seconds. Calculate the induced EMF in the solenoid.
Solution: To find the induced EMF (E), we use Faraday’s Law of Electromagnetic Induction:
𝐸=−𝑁 (ΔΦ / Δ𝑡)
- 𝑁 = 200 turns
- ΔΦ = 0.25 Weber – 0.05 Weber = 0.2 Weber
- Δ𝑡 = 0.2 seconds
Plugging in the values:
𝐸=−200×0.20.2=−200×1=−200 volts
Explanation: The negative sign indicates the direction of the induced EMF opposes the change in magnetic flux, as per Lenz’s Law. Thus, the induced EMF in the solenoid is 200 volts.
Example 2: Induced Voltage in a Moving Conductor
Problem: A conductor 1 meter long moves perpendicularly through a magnetic field at a speed of 3 meters per second. The magnetic field strength is 0.3 Tesla. Calculate the induced voltage across the conductor.
Solution: Here, the induced voltage (V) can also be calculated by considering the velocity of the conductor through the magnetic field:
𝑉=𝐵 × 𝑙 × 𝑣
Where:
- B = 0.3 Tesla (magnetic field strength)
- l = 1 meter (length of the conductor)
- 𝑣 = 3 meters per second (velocity)
Substituting the values:
𝑉=0.3×1×3=0.9 volts
Explanation: The conductor moving through the magnetic field experiences a force due to the Lorentz force law, which induces a voltage of 0.9 volts across it. This calculation shows how motion in a magnetic field can generate electricity, a principle used in many power generation system.
FAQs
What Is the Induced Current Voltage?
Induced current voltage refers to the voltage generated when a conductor moves through a changing magnetic field, per Faraday’s Law.
What Is the Formula for Induced Voltage in a Transformer?
The formula for induced voltage in a transformer is 𝐸=−𝑁ΔΦΔ𝑡E=−NΔtΔΦ, where 𝑁N is the number of coil turns.
What Is the Induced Voltage Rule?
The induced voltage rule, Lenz’s Law, states that induced voltage will always work to oppose the change in magnetic flux that produced it.
Share :
Practice Test
A solenoid with 1000 turns, length 50 cm, and cross-sectional area 4 cm² is subjected to a changing magnetic field of 0.2 T/s. What is the induced emf?
0.8 V
4 V
8 V
40 V
of 10
What is the induced voltage in a loop with an area of 0.1 m², with a magnetic field changing at a rate of 0.05 T/s?
0.005 V
0.01 V
0.005 V
0.1 V
of 10
A circular coil of 300 turns and radius 10 cm is placed in a magnetic field of 0.02 T which is perpendicular to the plane of the coil. If the field increases uniformly to 0.04 T in 0.1 seconds, what is the induced emf?
0.03 V
0.6 V
1.2 V
2.4 V
of 10
A rectangular loop of wire with dimensions 5 cm by 10 cm is in a magnetic field of 0.3 T. If the loop is rotated such that the angle with the field changes uniformly from 0° to 90° in 2 seconds, what is the average induced emf?
0.0375 V
0.075 V
0.15 V
0.3 V
of 10
In a 500-turn coil, the magnetic flux through each turn changes from 0.1 Wb to 0.2 Wb in 0.5 seconds. Calculate the induced emf.
50 V
100 V
200 V
300 V
of 10
If the magnetic flux through a coil with 1500 turns changes from 0.05 Wb to 0.1 Wb in 1 second, what is the induced emf?
50 V
75 V
100 V
150 V
of 10
A magnetic field through a coil of 200 turns decreases from 0.3 T to 0.1 T in 0.2 seconds. If the coil area is 0.01 m², what is the induced emf?
0.4 V
1 V
2 V
3 V
of 10
What is the induced voltage if a magnetic field of 0.2 T passes through a 500-turn coil with an area of 0.02 m², changing to 0.4 T in 0.25 seconds?
0.8 V
2.4 V
8 V
16 V
of 10
A 100-turn coil with an area of 0.01 m² is placed in a magnetic field of 0.05 T. If the field changes to 0.1 T in 0.2 seconds, what is the induced emf?
0.5 V
1 V
1.5 V
2 V
of 10