What is the unit Pascal (Pa) used to measure?
Energy
Force
Pressure
Power
of 10
Pascal – Practical Examples, Definition, Formula, Si Units, Uses
Pascal – Practical Examples, Definition, Formula, Si Units, Uses
Introduction
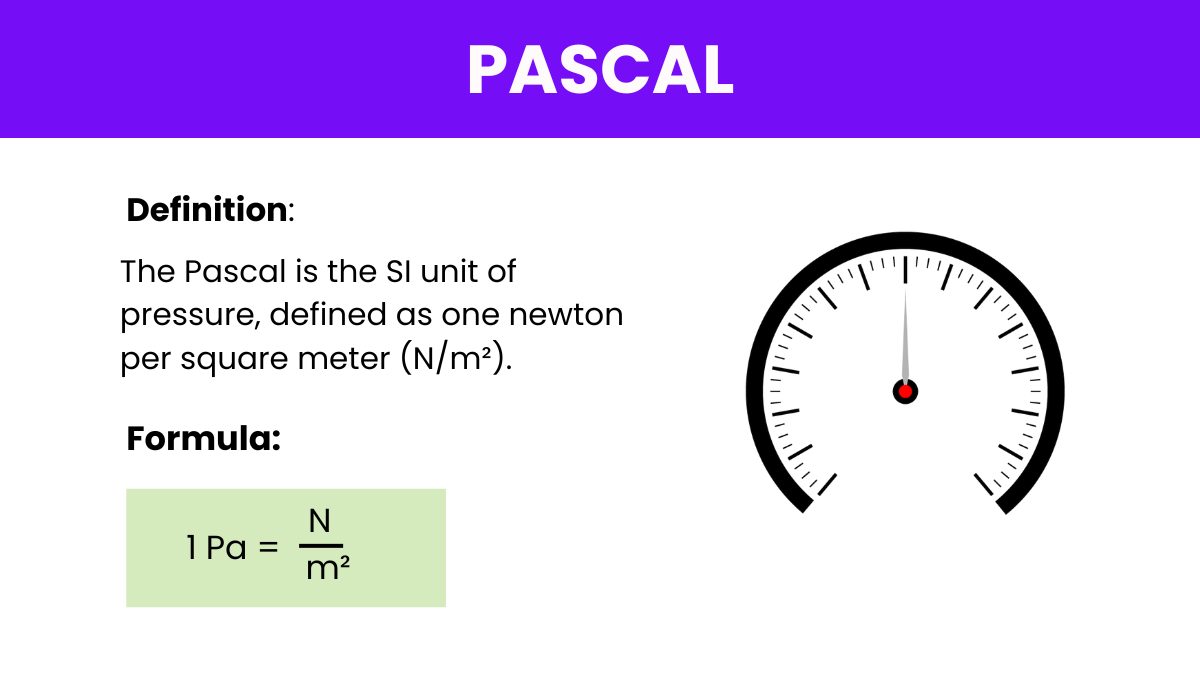
Pressure is a fundamental concept in physics, representing the force exerted on a surface per unit area. It’s measured using various units, including the Bar, and pound per square inch (psi). Among these, the pascal stands out as the SI unit of pressure, named after the French mathematician and physicist Blaise Pascal. It’s Units of Pressure defined as one newton of force per square meter, providing a precise and universal measure of pressure in scientific and engineering contexts. Understanding the pascal and its relationship to other pressure units like the bar and psi is essential for various applications, from atmospheric studies and hydraulic systems to material testing and medical diagnostics.
What is Pascal
Pascal Formula
Practical Example for the Pascal Formula
- Hydraulic System: If a hydraulic cylinder exerts a force of 5000 Newtons over an area of 0.05 square meters, the pressure generated is: Pressure (Pa) = Force (N)Area (m2) = 5000 N0.05 m2 = 100,000 Pressure (Pa) = Area (m2)Force (N) = 0.05m25000N = 100,000Pa.
- Tire Pressure: If a tire has a force of 2000 Newtons acting on its inner surface with an area of 0.002 square meters, the pressure inside the tire is: Pressure (Pa) = Force (N)Area (m2) = 2000 N0.002 m2 = 1,000,000 Pressure (Pa) = Area (m2)Force (N) = 0.002m22000N=1,000,000Pa.
- Atmospheric Pressure: With a force of approximately 10,000 Newtons acting on each square meter of the Earth’s surface due to atmospheric pressure, the pressure at sea level is: Pressure (Pa) = Force (N)Area (m2) = 10,000 N1 m2 = 10,000 PaPressure (Pa) = Area (m2)Force (N) = 1m210,000N = 10,000Pa.
- Water Bottle: If a water bottle has a force of 20 Newtons acting on its base with an area of 0.01 square meters, the pressure exerted on the table is: Pressure (Pa) = Force (N)Area (m2) = 20 N0.01 m2 = 2000 Pressure (Pa) = Area (m2)Force (N) = 0.01m220N = 2000Pa
- Diving Depth: At a depth of 30 meters in the ocean, the pressure on a diver’s body is approximately: Pressure (Pa) = Density of Water × Gravitational Acceleration × DepthPressure (Pa) = Density of Water × Gravitational Aceleration × Depth The pressure due to depth alone can be calculated using the formula for hydrostatic pressure.
- Balloon Inflation: Inflating a balloon with a force of 5 Newtons over an area of 0.0025 square meters results in a pressure of: Pressure (Pa) = Force (N)Area (m2) = 5 N0.0025 m2 = 2000 Pressure (Pa) = Area (m2)Force (N) = 0.0025m25N = 2000Pa
- Car Brake System: If the brake pedal exerts a force of 500 Newtons on the brake pads with an area of 0.005 square meters, the pressure generated in the brake system is: Pressure (Pa)=Force (N)Area (m2) = 500 N0.005 m2 = 100,000 Pressure (Pa) = Area (m2)Force (N) = 0.005m2500N = 100,000Pa
- Fire Hose: When water flows through a fire hose with a force of 2000 Newtons and an area of 0.02 square meters, the pressure at the nozzle is: Pressure (Pa) = Force (N)Area (m2) = 2000 N0.02 m2 = 100,000 Pressure (Pa) = Area (m2)Force (N) = 0.02m22000N = 100,000Pa
- Airplane Wings: If the lift force generated by an airplane wing is 50,000 Newtons over an area of 100 square meters, the pressure exerted by the wing is: Pressure (Pa) = Force (N)Area (m2) = 50,000 N100 m2 = 500 Pressure (Pa) = Area (m2)Force (N) = 100m250,000N = 500Pa
- Blood Pressure: A person’s blood pressure may be measured as 120/80 millimeters of mercury (mmHg), which can be converted to pascals using appropriate conversion factors.
Pascal’s Law
Formula: The formula expressing Pascal’s law:
Where:
is the pressure exerted on the fluid,
is the force applied to the fluid, and
is the area over which the force is applied.
Example of Pascal’s Law
Hydraulic Jack
A common example of Pascal’s law in action is demonstrated by the operation of a hydraulic jack.
In a hydraulic jack, there are two connected pistons of different sizes—one large and one small—separated by a closed system filled with hydraulic fluid. When a force is applied to the smaller piston by pushing down on the jack handle, according to Pascal’s law, this force is transmitted through the fluid uniformly in all directions.
As the force is transmitted through the fluid, it exerts pressure on the larger piston. Because the larger piston has a greater surface area, the pressure applied results in a much larger force being exerted upward. This allows the hydraulic jack to lift heavy objects with relatively little effort applied to the handle.
In this example, Pascal’s law demonstrates how a small force can be magnified to exert a much greater force using hydraulic systems. This principle is fundamental to the operation of various hydraulic machinery, including lifts, presses, and braking systems in vehicles.
SI multiples of Pascal
| Prefix | Symbol | Multiplier | Value in Pascals (Pa) |
|---|---|---|---|
| Megapascal | MP | 10⁶ | 1 MPa = 1,000,000 |
| Kilopascal | kPa | 10³ | 1 kPa = 1,000 Pa |
| Hectopascal | hPa | 10² | 1 hPa = 100 Pa |
| Decapascal | daPa | 10¹ | 1 daPa = 10 Pa |
| Decipascal | dPa | 10⁻¹ | 1 dPa = 0.1 Pa |
| Centipascal | cPa | 10⁻² | 1 cPa = 0.01 Pa |
| Millipascal | mPa | 10⁻³ | 1 mPa = 0.001 Pa |
| Micropascal | μPa | 10⁻⁶ | 1 pPa = 0.000001 Pa |
| Nanopascal | nPa | 10⁻⁹ | 1 nPa = 0.00000000 |
| Picopascal | pPa | 10⁻¹² | 1 pPa = 0.00000000000 |
| Femtopascal | fPa | 10⁻¹⁵ | 1 fPa = 0.00000000000000 |
Conversion of Pascal into other Units
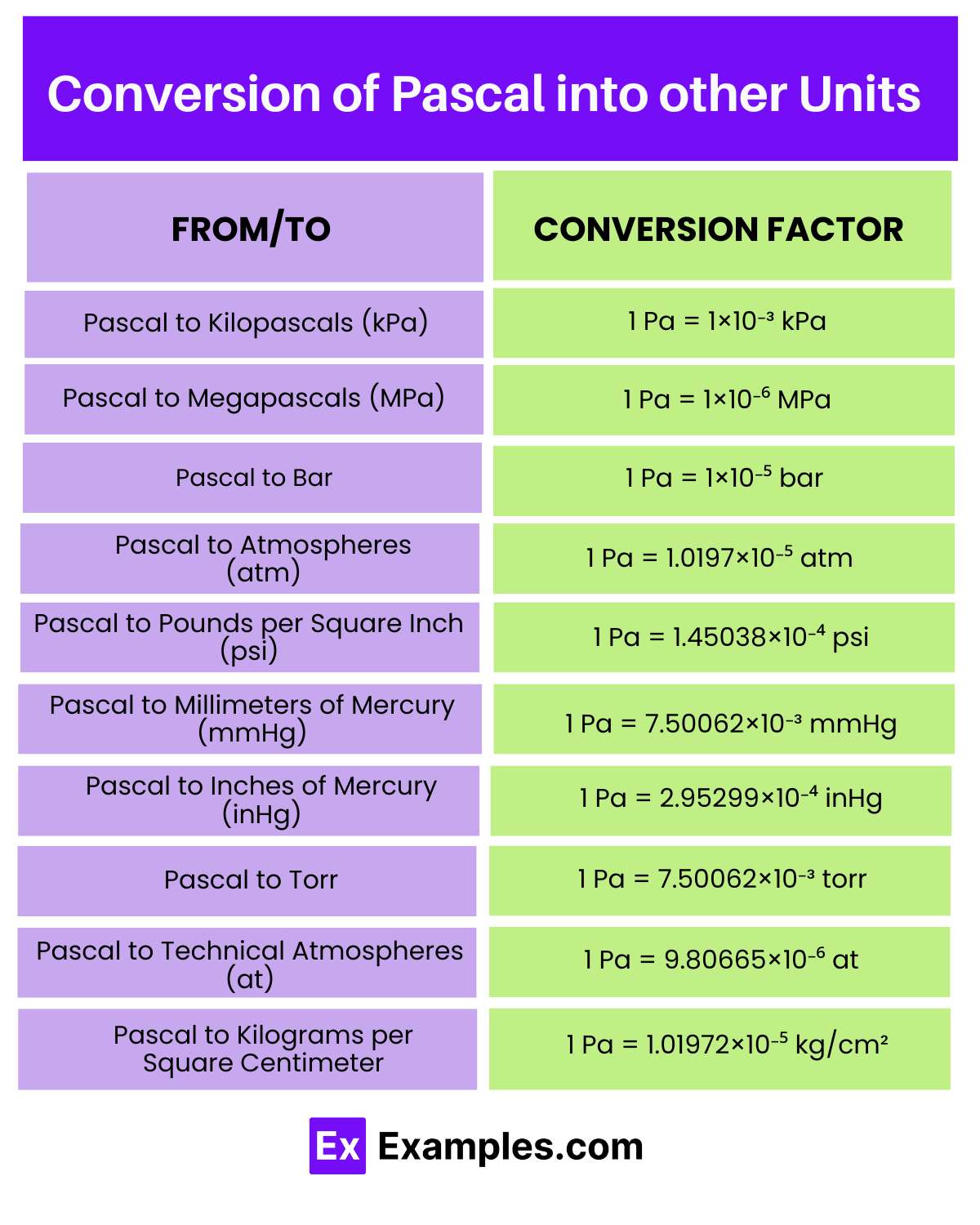
| From/To | Conversion Factor | Example Conversion |
|---|---|---|
| Pascal to Kilopascals (kPa) | 1 Pa = 1×10⁻³ kPa | 10 Pa = 1×10⁻² kPa |
| Pascal to Megapascals (MPa) | 1 Pa = 1×10⁻⁶ MPa | 10 Pa = 1×10⁻⁵ MPa |
| Pascal to Bar | 1 Pa = 1×10⁻⁵ bar | 10 Pa = 1×10⁻⁴ bar |
| Pascal to Atmospheres (atm) | 1 Pa = 1.0197×10⁻⁵ atm | 10 Pa = 1.0197×10⁻⁴ atm |
| Pascal to Pounds per Square Inch (psi) | 1 Pa = 1.45038×10⁻⁴ psi | 10 Pa = 1.45038×10⁻³ psi |
| Pascal to Millimeters of Mercury (mmHg) | 1 Pa = 7.50062×10⁻³ mmHg | 10 Pa = 7.50062×10⁻² mmHg |
| Pascal to Inches of Mercury (inHg) | 1 Pa = 2.95299×10⁻⁴ inHg | 10 Pa = 2.95299×10⁻³ inHg |
| Pascal to Torr | 1 Pa = 7.50062×10⁻³ torr | 10 Pa = 7.50062×10⁻² torr |
| Pascal to Technical Atmospheres (at) | 1 Pa = 9.80665×10⁻⁶ at | 10 Pa = 9.80665×10⁻⁵ at |
| Pascal to Kilograms per Square Centimeter | 1 Pa = 1.01972×10⁻⁵ kg/cm² | 10 Pa = 1.01972×10⁻⁴ kg/cm² |
Notes
- Kilopascals (kPa): Multiply the pressure in Pascals by 10−310−3 to obtain the value in kilopascals.
- Megapascals (MPa): Multiply the pressure in Pascals by 10−610−6 to obtain the value in megapascals.
- Bar: Multiply the pressure in Pascals by 10−510−5 to obtain the value in bars.
- Atmospheres (atm): The pressure in atmospheres is approximately 1.0197×10−51.0197×10−5 times the pressure in Pascals.
- Pounds per Square Inch (psi): The pressure in pounds per square inch is approximately 1.45038×10−41.45038×10−4 times the pressure in Pascals.
- Millimeters of Mercury (mmHg): The pressure in millimeters of mercury is approximately 7.50062×10−37.50062×10−3 times the pressure in Pascals.
- Inches of Mercury (inHg): The pressure in inches of mercury is approximately 2.95299×10−42.95299×10−4 times the pressure in Pascals.
- Torr: The pressure in torr is approximately 7.50062×10−37.50062×10−3 times the pressure in Pascals.
- Technical Atmospheres (at): The pressure in technical atmospheres is approximately 9.80665×10−69.80665×10−6 times the pressure in Pascals.
- Kilograms per Square Centimeter: The pressure in kilograms per square centimeter is approximately 1.01972×10−51.01972×10−5 times the pressure in Pascals.
Pascal to Kilopascals (kPa)
Kilopascals are commonly used to measure pressure in various industrial and scientific applications. They are especially useful for quantifying pressures in fluid systems and hydraulic machinery.
Pascal to Megapascals (MPa)
Megapascals represent even higher pressures, often encountered in engineering contexts such as structural analysis, material testing, and high-pressure fluid systems.
Pascal to Bar
Bars are a convenient unit for expressing atmospheric pressure and are frequently used in meteorology and aviation for weather forecasting and aircraft instrumentation.
Pascal to Atmospheres (atm)
Atmospheres are a unit of pressure often used in meteorology and oceanography to describe atmospheric and underwater pressures. They provide a measure of the pressure exerted by the Earth’s atmosphere at sea level.
Pascal to Pounds per Square Inch (psi)
Pounds per square inch is a unit commonly used in engineering, particularly in the United States. It’s frequently employed in the automotive, aerospace, and manufacturing industries to specify pressure in hydraulic and pneumatic systems.
Pascal to Millimeters of Mercury (mmHg)
Millimeters of mercury are commonly used in medical and scientific fields, particularly in barometric measurements and blood pressure readings.
Pascal to Inches of Mercury (inHg)
Inches of mercury are similar to millimeters of mercury but are more commonly used in North America. They are widely utilized in aviation, meteorology, and engineering for pressure measurements.
Pascal to Torr
Torr is another unit commonly used in scientific and engineering applications, particularly in vacuum technology and gas pressure measurements. It is equivalent to the pressure exerted by a column of mercury 1 millimeter high under standard conditions.
Pascal to Technical Atmospheres (at)
Technical atmospheres are used in various industries, including manufacturing, chemistry, and materials science, to quantify pressure in pressurized systems and equipment.
Pascal to Kilograms per Square Centimeter
Kilograms per square centimeter is a unit often used in engineering and manufacturing contexts, especially in countries where the metric system is prevalent. It provides a measure of pressure relative to the weight of a standard kilogram distributed over a square centimeter area.
Practical Application Example of Pascal
Pascals find practical application across diverse fields due to their versatility in measuring pressure. In engineering, they are crucial for designing and analyzing structures, ensuring their integrity under varying loads. In hydraulics and pneumatics, Pascals govern fluid and gas pressures, essential for operating machinery and systems efficiently. Meteorologists employ Pascals to gauge atmospheric pressure, aiding in weather prediction and climate modeling. Medical professionals utilize Pascals in blood pressure measurements, diagnosing cardiovascular health and guiding treatment. In manufacturing, Pascals help maintain precise pressure conditions in industrial processes, ensuring product quality and efficiency. Additionally, Pascals play a vital role in aviation, where accurate pressure measurements are critical for aircraft performance and safety. Overall, Pascals serve as a fundamental unit for quantifying pressure across numerous applications, contributing to advancements in science, technology, and everyday life.
What are the Uses of Pascal?
Engineering Applications
- Structural Engineering: Pascals are crucial for analyzing stresses and strains in building materials, ensuring structural integrity.
- Mechanical Engineering: Used in designing and testing machinery, such as engines and turbines, to determine optimal pressure conditions.
- Civil Engineering: Pascals aid in designing infrastructure like bridges and dams, considering pressure variations and load distributions.
Fluid Dynamics and Hydraulics
- Hydraulic Systems: Pascals govern fluid pressure in hydraulic machinery, such as lifts and brakes, ensuring smooth operation.
- Pneumatic Systems: Utilized in pneumatic systems for controlling gas pressure in applications like air compressors and HVAC systems.
Atmospheric and Environmental Sciences
- Meteorology: Used to measure atmospheric pressure, assisting in weather forecasting and climate studies.
- Oceanography: Pascals are employed to quantify pressure variations in oceanic environments, influencing ocean currents and marine life.
Medical and Health Sciences
- Blood Pressure Monitoring: Crucial in measuring blood pressure levels, aiding in diagnosing hypertension and cardiovascular diseases.
- Respiratory Mechanics: Used to assess lung function and diagnose respiratory disorders by measuring airway pressures.
Industrial and Manufacturing Processes
- Quality Control: Pascals ensure precise pressure conditions in manufacturing processes, maintaining product quality and consistency.
- Process Engineering: Employed to regulate pressure in chemical processes, such as distillation and fermentation, optimizing production efficiency.
Aviation and Aerospace
- Aircraft Instrumentation: Pascals are used in aircraft instrumentation to monitor cabin pressure, ensuring passenger comfort and safety.
- Aerodynamics: Critical for understanding air pressure dynamics around aircraft surfaces, influencing aerodynamic performance and flight stability.
FAQs
What role does atmospheric pressure, measured in Pascals, play in weather patterns and climate dynamics?
Atmospheric pressure, measured in Pascals, influences weather patterns and climate dynamics by driving air circulation and the formation of weather systems. Understanding changes in atmospheric pressure helps meteorologists predict weather phenomena and assess climate trends.
What are some everyday examples where the Pascal unit is relevant?
Everyday examples of Pascal unit applications include tire pressure gauges, blood pressure monitors, and barometers. These devices rely on accurate pressure measurements to ensure safety, health monitoring, and weather prediction.
What is the significance of the Pascal unit in pressure measurement?
The Pascal unit is significant because it provides a standardized measure of pressure across various scientific and engineering disciplines, enabling precise quantification of forces exerted by fluids and gases.
Share :
Practice Test
1 Pascal is equivalent to:
1 Newton per meter
1 Newton per square meter
1 Joule per second
1 Coulomb per second
of 10
If a force of 50 Newtons is applied over an area of 5 square meters, what is the pressure?
5 Pa
10 Pa
50 Pa
500 Pa
of 10
Which instrument is commonly used to measure pressure?
Thermometer
Ammeter
Voltmeter
Barometer
of 10
In which of the following fields is the Pascal commonly used?
Meteorology
Thermodynamics
Electronics
Astronomy
of 10
If the pressure on a surface is 300 Pa and the area is 2 m², what is the force applied?
150 N
300 N
600 N
900 N
of 10
Which of the following is NOT a unit of pressure?
Pascal
Bar
Torr
Watt
of 10
A tire has a pressure of 200 kPa. What is this pressure in Pascals?
2000 Pa
20000 Pa
200000 Pa
2000000 Pa
of 10
Which law is closely associated with the use of the Pascal unit?
Newton's First Law
Boyle's Law
Pascal's Law
Ohm's Law
of 10
Which of the following pressures is equal to 1 atm?
101.3 Pa
1013 Pa
10130 Pa
101300 Pa
of 10