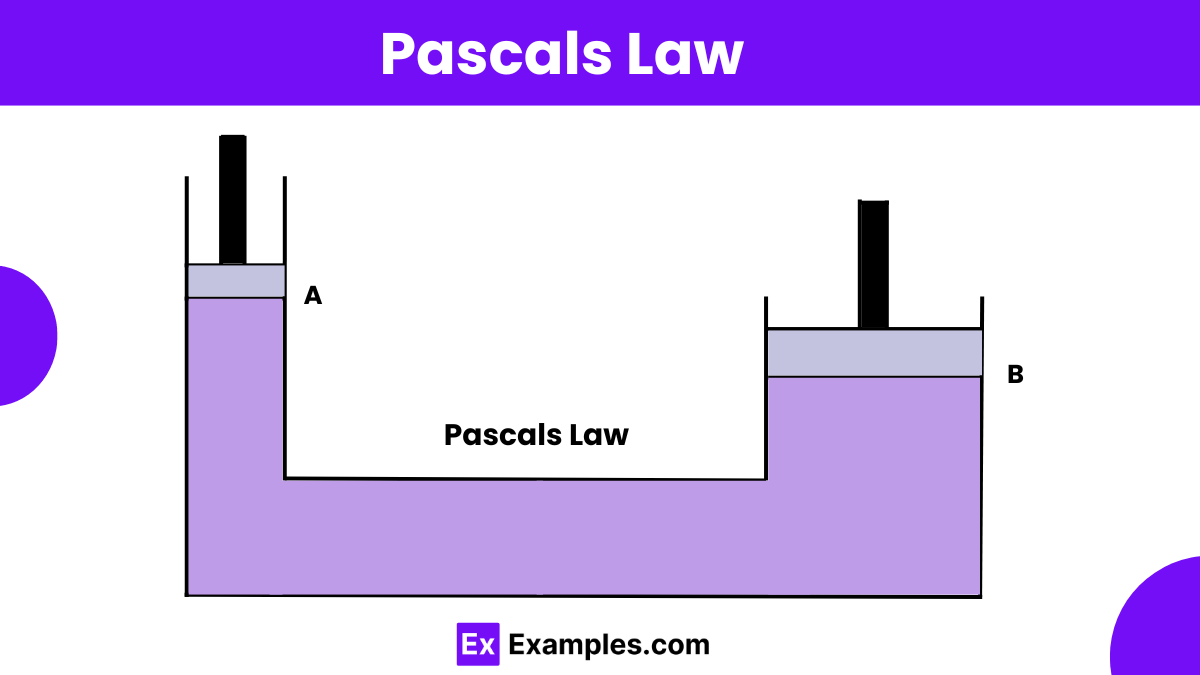
Which of the following statements best describes Pascal's Law?
Pressure is the same at all points in a fluid.
Pressure applied to a confined fluid is transmitted equally in all directions.
Fluids flow from high to low pressure.
The pressure in a fluid decreases with depth.