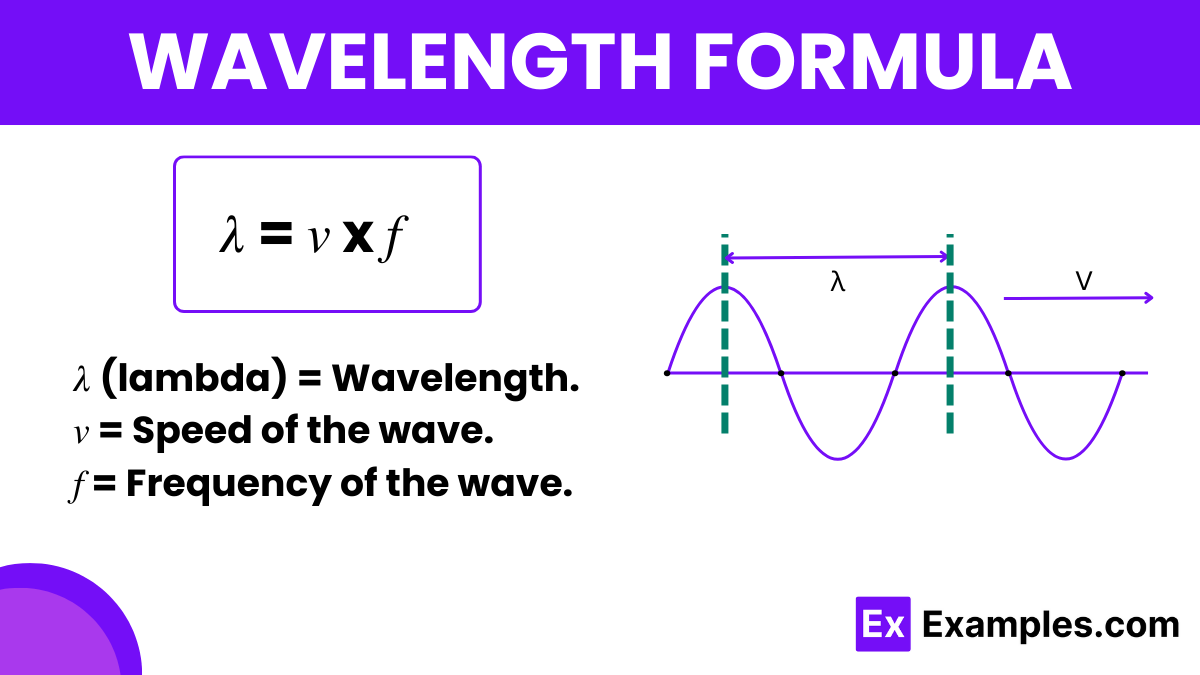
Wavelength Formula

What is Wavelength Formula?

The wavelength formula is essential in physics for calculating the distance between repeating units of a wave pattern. It is commonly symbolized by the Greek letter lambda (λ) and is crucial in various fields of science, especially in optics, acoustics, and electromagnetic theory. This formula helps in determining the physical properties of waves, such as their speed and frequency.

The wavelength formula is defined as

𝜆 = 𝑣 x 𝑓

𝜆 (lambda) represents the wavelength.
𝑣 is the speed of the wave.
𝑓 is the frequency of the wave.

This means that the wavelength is the ratio of the speed at which the wave propagates through a medium to the frequency with which the wave cycles occur. Essentially, it tells us how long one cycle of the wave is in physical space.

The concept of wavelength was first rigorously analyzed by physicists such as Isaac Newton and Thomas Young, but the precise formulation of the wavelength formula as we know it today was developed through the work of multiple scientists over time.

Derivation of Wavelength Formula

Step 1: Understanding Basic Wave Properties

First, let’s define the terms involved in the formula:

Wavelength (𝜆) is the distance over which the wave’s shape repeats. It is measured in meters (m).
Speed (v) is the rate at which the wave propagates through a medium, expressed in meters per second (m/s).
Frequency (f) is the number of cycles of the wave that pass a fixed point in one second, measured in hertz (Hz).

Step 2: Relating Speed, Frequency, and Wavelength

Consider a wave moving through a medium. The speed of the wave tells us how fast a single point on the wave, such as a crest, travels through the medium. In one second, the wave travels a distance equal to its speed, 𝑣v.

Now, if we consider the frequency, f, it indicates how many complete waves pass a point in one second. If each wave has a length of 𝜆λ, then the total distance covered by 𝑓 waves in one second is

𝑓 × 𝜆

According to the definition of speed, this distance must also equal the speed of the wave:

𝑣 = 𝑓 × 𝜆

Step 3: Solving for Wavelength

To find the formula for wavelength, we rearrange the equation above:

𝜆 = 𝑣 / 𝑓

This equation shows that the wavelength is the speed of the wave divided by its frequency. This relationship is crucial because it allows physicists to calculate any one of these three variables if the other two are known.

This derivation not only highlights the interconnected nature of speed, frequency, and wavelength in wave physics but also provides a clear mathematical framework for analyzing waves in various mediums. Whether it’s sound waves in air or electromagnetic waves in a vacuum, this formula remains a key tool in the field of physics.

Applications of Wavelength Formula

Telecommunications: Engineers use the formula to design antennas that properly transmit and receive radio waves at desired frequencies.
Medical Imaging: Technicians calculate the wavelength of ultrasound waves to create images of internal organs.
Astronomy: Astronomers apply the wavelength formula to determine the properties of electromagnetic waves coming from stars and galaxies.
Music and Acoustics: Musicians and sound engineers use the wavelength formula to understand sound wave properties and design musical instruments and concert venues.
Wireless Networking: This formula helps in setting up Wi-Fi networks by determining optimal frequencies for signal clarity and range.
Radar Systems: The wavelength of radio waves affects radar precision, which is vital for aviation safety and weather forecasting.

Example Problems on Wavelength Formula

Problem 1: Calculating Wavelength of a Sound Wave

Problem Statement: A sound wave travels through air at a speed of 340 m/s with a frequency of 1700 Hz. What is the wavelength of this sound wave?

Solution: Using the wavelength formula 𝜆=𝑣 x 𝑓

𝜆 = 340 m/s x 1700 Hz = 0.2 meters

Problem 2: Finding Frequency from Wavelength and Speed

Problem Statement: The wavelength of a light wave in a vacuum is 500 nm (nanometers), and the speed of light is approximately 3×1083×108 m/s. What is the frequency of this light wave?

Solution: First, convert the wavelength from nanometers to meters:

500 nm = 500×10⁻⁹.

Now, apply the formula to find the frequency f,

𝑓 = 𝑣 / 𝜆=3×108 m/s / (500×10⁻⁹ m) = 6×10¹⁴ Hz

Problem 3: Determining Wave Speed

Problem Statement: An FM radio station broadcasts at a frequency of 90.5 MHz. If the wavelength of these radio waves is 3.3 meters, what is the speed of the waves?

Solution: First, convert MHz to Hz:

90.5 MHz = 90.5 × 10⁶ Hz.

Using the wavelength formula to calculate speed 𝑣,

𝑣 = 𝜆 × 𝑓= 3.3 m × 90.5×10⁶ Hz=298.65×10⁶ m/s =

FAQs

How Do You Calculate Wavelength from Frequency?

To calculate wavelength (λ) from frequency (f), use the formula: 𝜆=𝑣 / 𝑓, where 𝑣 is the wave speed.

What Does λ Mean in Physics?

In physics, λ (lambda) represents the wavelength of a wave, indicating the distance over which the wave’s shape repeats.

Is Wavelength Equal to Frequency?

No, wavelength is not equal to frequency. Wavelength is the distance a wave travels per cycle, while frequency is the number of cycles per second.

Wavelength Formula