GCF of 12 and 36
GCF of 12 and 36
The greatest common factor (GCF) of 12 and 36 is 12. This value is derived using various methods such as prime factorization, listing common factors, or applying the Euclidean algorithm. When prime factorizing, 12 is broken down to 2²×3 and 36 to 2²×3². The common prime factors are 2 and 3, with the lowest powers being 2²and 3¹, resulting in 2² × 3 =12 . Listing the factors of 12 (1, 2, 3, 4, 6, 12) and 36 (1, 2, 3, 4, 6, 9, 12, 18, 36) also highlights that 12 is the highest factor both numbers share. Using the Euclidean algorithm, which involves successive divisions, similarly confirms that 12 is the largest number that divides both 12 and 36 without leaving a remainder, establishing it as their GCF.
GCF of 12 and 36
GCF of 12 and 36 is 12.
GCF of 12 and 36 by Prime Factorization Method.
To find the greatest common factor (GCF) of 12 and 36 using the prime factorization method:
Step 1: Prime factorize both numbers:
For 12: 12 = 2² × 3
For 36: 36 = 2² × 3²
Step 2: Identify the common prime factors and their lowest powers:
The common prime factors between 12 and 36 are 2 and 3. The lowest powers are 222^222 and 313^131.
Step 3: Multiply the common prime factors with their lowest powers to determine the GCF:
GCF = 2² × 3¹ = 4 × 3 =12
Therefore, the greatest common factor (GCF) of 12 and 36 by prime factorization method is 12.
GCF of 12 and 36 by Long Division Method.
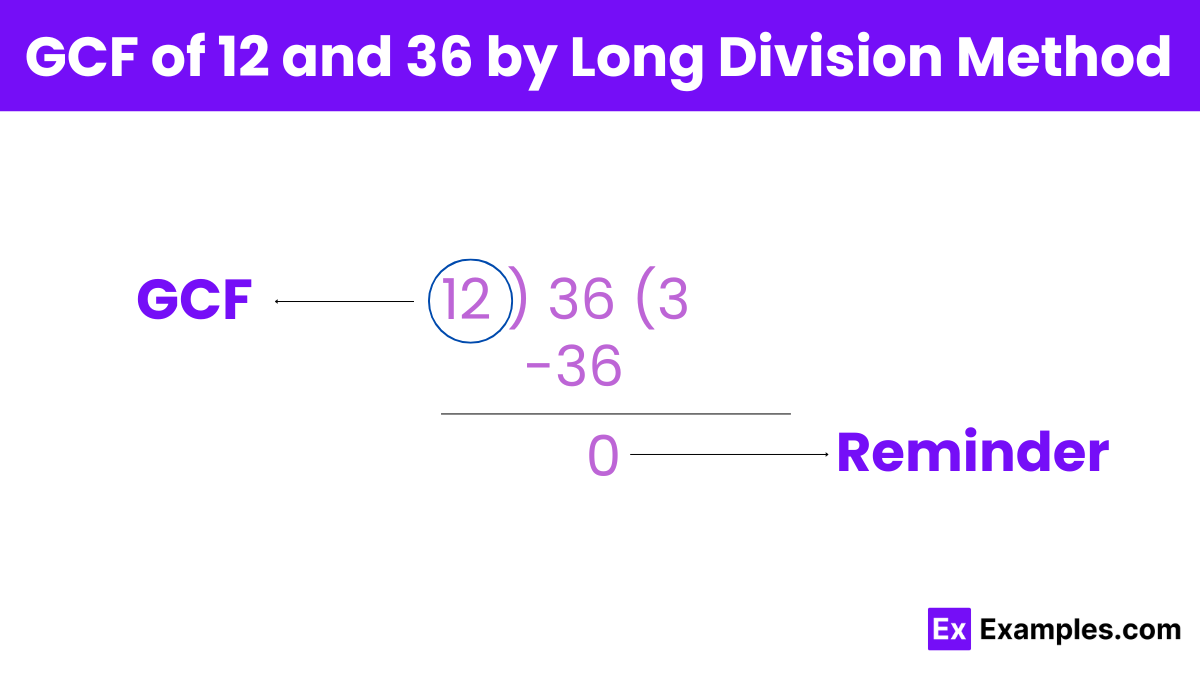
To find the greatest common factor (GCF) of 12 and 36 using the long division method:
Step 1: Start by dividing the larger number (36) by the smaller number (12).
36 ÷ 12 = 3 with a remainder of 0.
Since there is no remainder, the division process stops here.
Step 2: The divisors at this step, where the remainder becomes zero, is the greatest common factor (GCF).
GCF = 12.
Therefore, the greatest common factor (GCF) of 12 and 36 by the long division method is 12.
GCF of 12 and 36 by Listing Common Factors.
To find the greatest common factor (GCF) of 12 and 36 by listing common factors:
Step 1: List the factors of each number.
Factors of 12: 1, 2, 3, 4, 6, 12
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Step 2: Identify the common factors.
Common factors: 1, 2, 3, 4, 6, 12
Step 3: Determine the greatest common factor.
The highest number in the list of common factors is 12.
How do you calculate the GCF of 12 and 36?
You can calculate the GCF using methods like prime factorization, listing common factors, or long division.
Can the GCF of 12 and 36 be larger than both numbers?
No, the GCF is always less than or equal to the smallest number.
What other methods are there to find the GCF of 12 and 36 besides prime factorization?
Long division and listing common factors are other methods.
What is the fastest method to find the GCF of 12 and 36?
Listing common factors is quick and straightforward for small numbers.
Why is understanding the GCF important in mathematics?
It’s crucial for simplifying expressions and solving problems involving ratios.
What mathematical concept is closely related to the GCF?
The Least Common Multiple (LCM) is also closely related to the GCF.
Share :
