GCF of 30 and 36
GCF of 30 and 36
The greatest common factor (GCF) of 30 and 36 is 6. To find the GCF, one can utilize methods such as prime factorization, listing common factors, or employing the Euclidean algorithm. By analyzing the prime factorization of both numbers, it becomes evident that they share common prime factors, with the lowest power of 2 and 3 being 1 for both. Therefore, the GCF is determined as the product of these common prime factors raised to their lowest powers, resulting in a GCF of 6. This GCF represents the largest integer that divides both 30 and 36 without leaving a remainder, making it a crucial factor in simplifying fractions or finding common divisors.
GCF of 30 and 36
GCF of 30 and 36 is 6.
GCF of 30 and 36 by Prime Factorization Method.
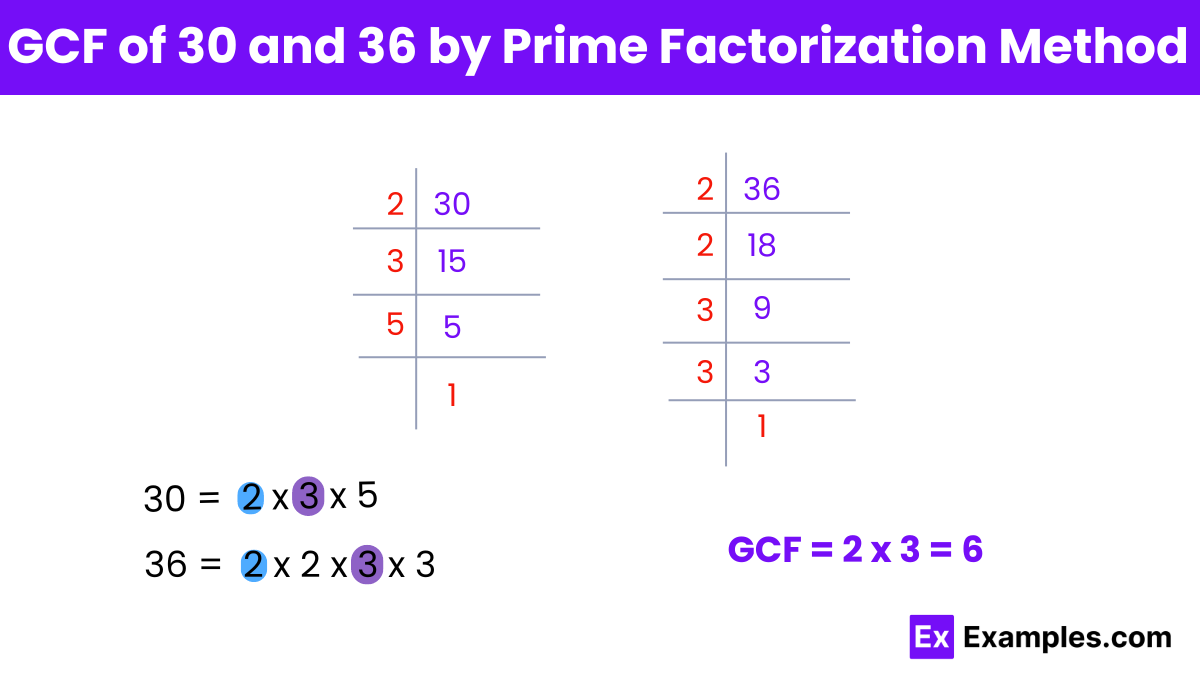
To find the greatest common factor (GCF) of 30 and 36 using the prime factorization method:
Step 1: Prime factorize both numbers:
For 30: 30 = 2×3×5
For 36: 36 = 2² × 3²
Step 2: Identify common prime factors and their lowest powers:
- Both 30 and 36 have common prime factors of 2 and 3. The lowest power of 2 is 1, and the lowest power of 3 is 1.
Step 3: Multiply the common prime factors with their lowest powers: GCF=2¹×3¹ = 2×3 = 6
Therefore, the greatest common factor (GCF) of 30 and 36 by prime factorization method is 6.
GCF of 30 and 36 by Long Division Method.
To find the greatest common factor (GCF) of 30 and 36 using the long division method:
Step 1: Start by dividing the larger number (36) by the smaller number (30).
36 ÷ 30 =1 with a remainder of 6.
Step 2: Then, take the divisor (30) and divide it by the remainder (6).
30 ÷ 6 = 5.
Step 3: Continue this process until there is no remainder.
6 ÷ 5 =1 with a remainder of 1.
5 ÷ 1 = 5.
1 ÷ 1 = 1.
Step 4: The last divisor before reaching 1 is the greatest common factor (GCF).
GCF = 6.
Therefore, the greatest common factor (GCF) of 30 and 36 by the long division method is 6.
GCF of 30 and 36 by Listing Common Factors.
To find the greatest common factor (GCF) of 30 and 36 by listing common factors:
Step 1: List the factors of each number.
Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Step 2: Identify the common factors. Common factors: 1, 2, 3, 6
Step 3: Determine the greatest common factor. GCF = 6.
Therefore, the greatest common factor (GCF) of 30 and 36 by listing common factors is 6.
How does the GCF of 30 and 36 relate to the concept of greatest common divisor?
The GCF of 30 and 36 is the greatest common divisor, as it represents the largest divisor common to both numbers.
How does the GCF of 30 and 36 help in simplifying fractions?
The GCF can be used to reduce fractions to their simplest form by dividing both the numerator and denominator by the GCF.
Can the GCF of 30 and 36 be larger than both numbers?
No, the GCF cannot be larger than both numbers. It is always a factor of both numbers.
How many common factors do 30 and 36 have?
30 and 36 have four common factors: 1, 2, 3, and 6.
How do you calculate the GCF of 30 and 36?
You can calculate the GCF of 30 and 36 using methods such as prime factorization, listing common factors, or long division.
Share :
