What is the Greatest Common Factor (GCF) of 16 and 32?
4
8
16
32
of 10
GCF of 16 and 32 – How to find in Different Ways
GCF of 16 and 32 – How to find in Different Ways
The greatest common factor (GCF) of 16 and 32 is 16. Both 16 and 32 share 16 as their largest common divisors. By prime factorizing 16 and 32, it’s evident that they both have 2 as a common factor, and 16 has an additional factor of 2. Thus, the GCF is determined by the common factors with the lowest power, which is 2 raised to the power of 4, resulting in 16. Therefore, 16 is the largest integer that divides both 16 and 32 without leaving a remainder, making it the greatest common factor.
GCF of 16 and 32
GCF of 16 and 32 is 16.
GCF of 16 and 32 by Prime Factorization Method.
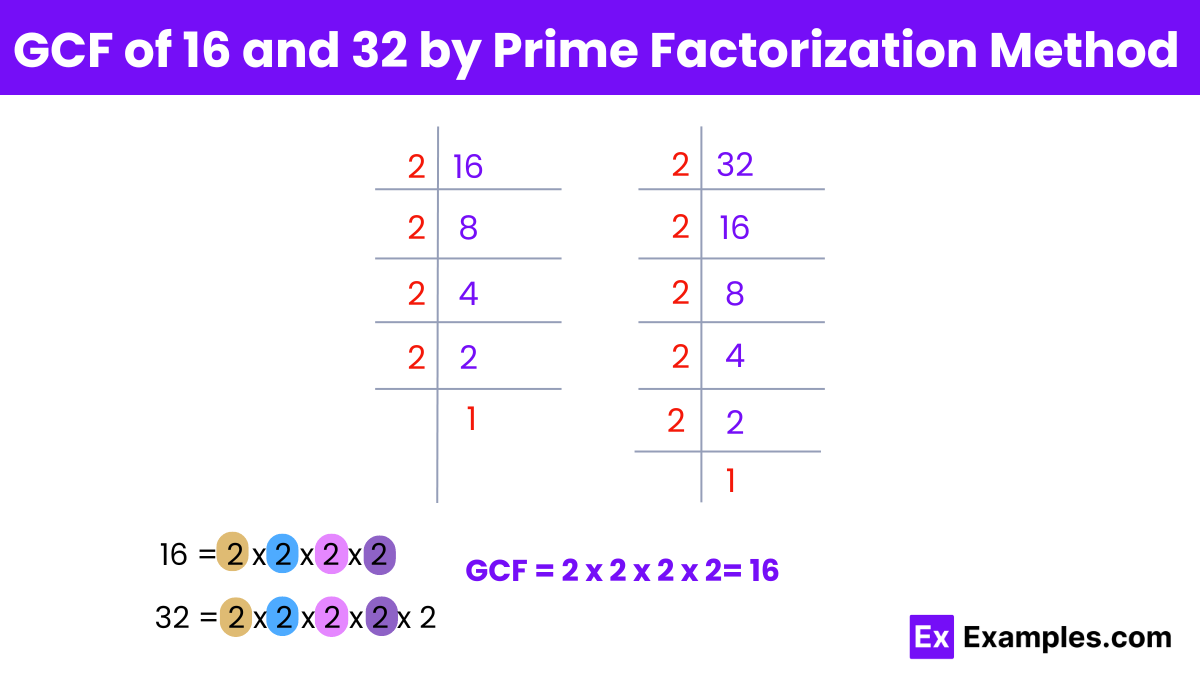
To find the greatest common factor (GCF) of 16 and 32 using the prime factorization method:
Step 1: Prime factorize both numbers:
For 16: 16 = 2⁴
For 32: 32 = 2⁵
Step 2: Identify the common prime factors and their lowest powers:
- Both 16 and 32 have the common prime factor of 2. The lowest power common to both is 2⁴.
Step 3: Multiply the common prime factors with their lowest powers:
GCF = 2⁴ = 16
Therefore, the greatest common factor (GCF) of 16 and 32 by prime factorization method is 16.
GCF of 16 and 32 by Long Division Method.
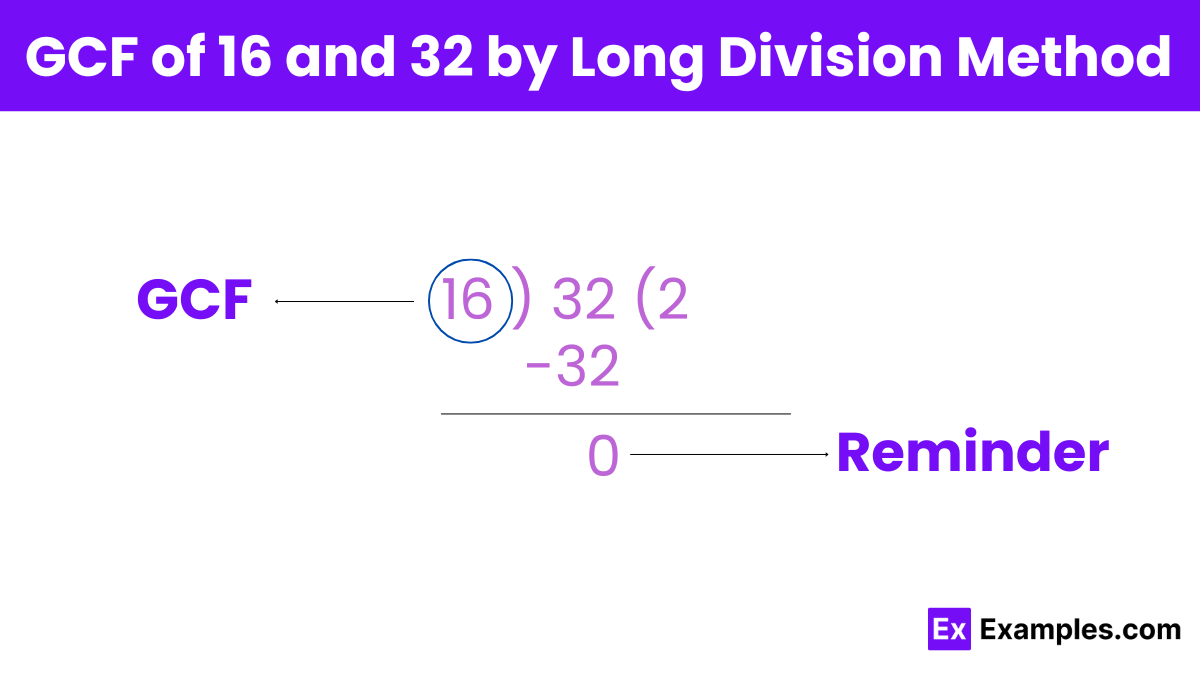
To find the greatest common factor (GCF) of 16 and 32 using the long division method:
Step 1: Start by dividing the larger number (32) by the smaller number (16).
32 ÷ 16 = 2 with a remainder of 0.
Since there is no remainder, the division process stops here.
Step 2: The divisor at this step, where the remainder becomes zero, is the greatest common factor.
GCF = 16.
Therefore, the greatest common factor (GCF) of 16 and 32 by the long division method is 16.
GCF of 16 and 32 by Listing Common Factors.
To find the greatest common factor (GCF) of 16 and 32 by listing common factors:
Step 1: List the factors of each number.
Factors of 16: 1, 2, 4, 8, 16
Factors of 32: 1, 2, 4, 8, 16, 32
Step 2: Identify the common factors.
Common factors: 1, 2, 4, 8, 16
Step 3: Determine the greatest common factor. GCF =16.
Therefore, the greatest common factor (GCF) of 16 and 32 by listing common factors is 16.
How do you calculate the GCF of 16 and 32?
You can calculate the GCF of 16 and 32 using methods such as prime factorization, listing common factors, or long division.
How many common factors do 16 and 32 have?
16 and 32 have five common factors: 1, 2, 4, 8, and 16.
Are there any other methods to find the GCF of 16 and 32 besides prime factorization?
Yes, methods such as listing common factors or using long division can also be used.
Is there a shortcut to find the GCF of numbers like 16 and 32?
Recognizing that both numbers are powers of 2 allows for quick identification of the GCF.
Can the GCF of 16 and 32 be found using algebraic methods?
Yes, the GCF can be found algebraically by factoring both numbers and identifying common factors.
How does the GCF of 16 and 32 relate to the concept of greatest common divisor?
The GCF of 16 and 32 is the greatest common divisor, as it represents the largest divisor common to both numbers.
Share :
Practice Test
Which of the following numbers is a common factor of both 16 and 32?
2
6
8
18
of 10
What is the smallest prime factor of the GCF of 16 and 32?
1
2
3
4
of 10
Which number is the largest common factor of 16 and 32?
4
8
16
32
of 10
How many factors does the GCF of 16 and 32 have?
2
3
4
5
of 10
Which pair of numbers has the same GCF as 16 and 32?
8 and 16
10 and 20
24 and 36
14 and 28
of 10
If you subtract the GCF of 16 and 32 from 32, what is the result?
14
15
16
17
of 10
What is the GCF of 16 and 32 multiplied by 2?
20
24
30
32
of 10
What is the result of dividing the GCF of 16 and 32 by 4?
2
4
6
8
of 10
What is the sum of the GCF of 16 and 32 and the number 8?
20
24
28
32
of 10