What is the Greatest Common Factor (GCF) of 18 and 30?
2
3
6
9
of 10
GCF of 18 and 30 – How to find in Different Ways
GCF of 18 and 30 – How to find in Different Ways
To find the Greatest Common Factor (GCF) of 18 and 30, list the factors of each numbers: the factors of 18 are 1, 2, 3, 6, 9, and 18, while the factors of 30 are 1, 2, 3, 5, 6, 10, 15, and 30. The common factors are 1, 2, 3, and 6, with the greatest common factor being 6. Using the prime factorization method, 18 can be expressed as 2 × 3² and 30 as 2 × 3 × 5, confirming that the common prime factors are 2 and 3. Multiplying these common prime factors (2 × 3) also gives the GCF as 6. Thus, the GCF of 18 and 30 is 6.
GCF of 18 and 30
GCF of 18 and 30 is 6 .
Methods to Find GCF of 18 and 30
- Prime Factorization Method
- Long Division Method
- Listing Common Factors
GCF of 18 and 30 by Prime Factorization Method.
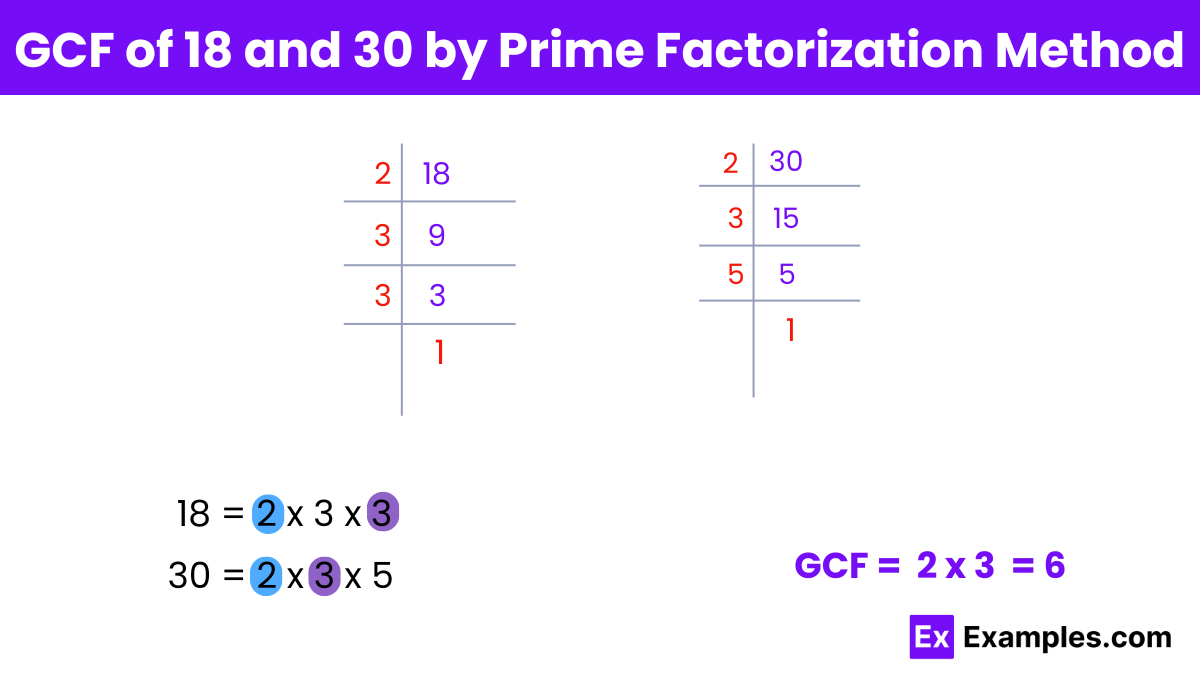
To find the Greatest Common Factor (GCF) of 18 and 30 using the prime factorization method, follow these steps:
Step 1: Find the prime factorization of each number
Prime factorization of 18:
18 = 2 × 3 × 3 = 2 × 3²
Prime factorization of 30:
30 = 2 × 3 × 5
Step 2: Identify the common prime factors
The common prime factors of 18 and 30 are 2 and 3.
Step 3: Multiply the common prime factors
The lowest powers of the common prime factors are 2 and 3. Therefore, multiply these together: 2 × 3 = 6.
GCF of 18 and 30 by Long Division Method.
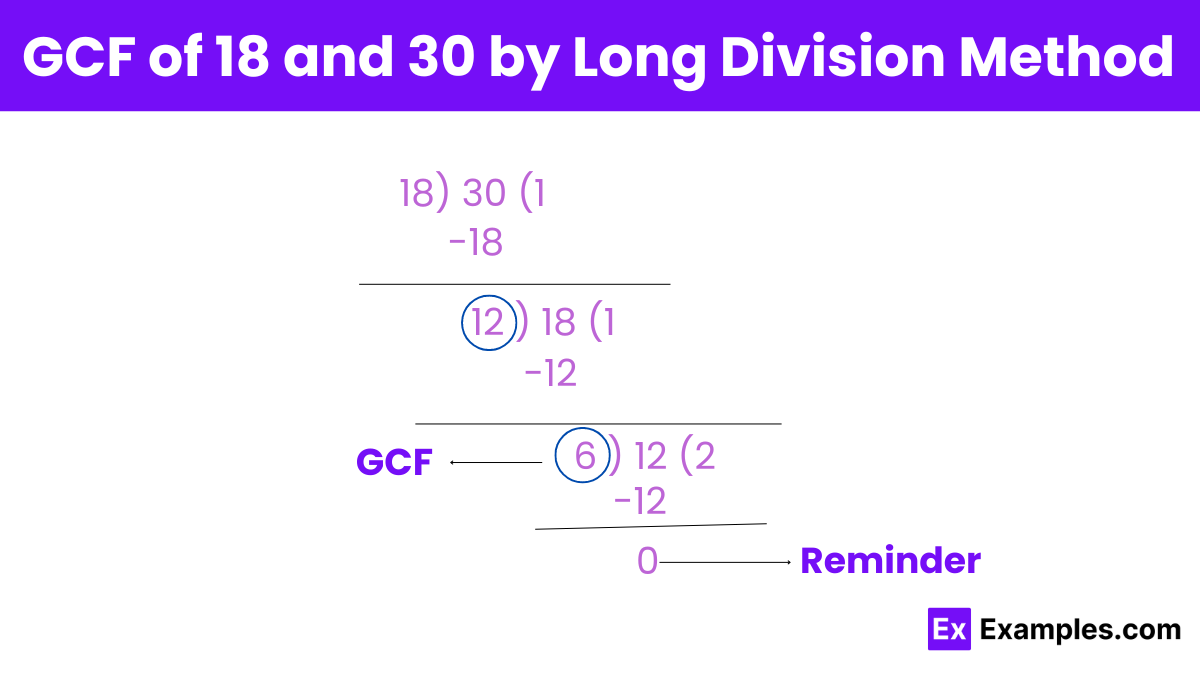
To find the Greatest Common Factor (GCF) of 18 and 30 using the long division method, follow these steps:
Step 1: Divide the larger number by the smaller number
30 ÷ 18 = 1 with a remainder of 12.
Step 2: Replace the larger number with the smaller number, and the smaller number with the remainder
Now, we have 18 and 12.
Step 3: Repeat the division
18 ÷ 12 = 1 with a remainder of 6.
Step 4: Continue the process
12 ÷ 6 = 2 with a remainder of 0.
Step 5: When the remainder is 0, the divisors is the GCF
The last non-zero remainder is 6. So, the GCF of 18 and 30 is 6.
GCF of 18 and 30 by Listing Common Factors.
To find the Greatest Common Factor (GCF) of 18 and 30 by listing common factors, follow these steps:
Step 1: List the factors of each number
Factors of 18:
1, 2, 3, 6, 9, 18
Factors of 30:
1, 2, 3, 5, 6, 10, 15, 30
Step 2: Identify the common factors
Common factors of 18 and 30:
1, 2, 3, 6
Step 3: Determine the greatest common factor
The largest common factor is 6. Therefore, the GCF of 18 and 30 is 6.
What if the GCF of 18 and 30 is used in real-life situations?
It helps in tasks such as reducing ratios and simplifying fractions for practical applications.
Can the GCF be zero?
No, the GCF is never zero.
What is the least common multiple (LCM) of 18 and 30?
The LCM of 18 and 30 is 90.
How do you verify the GCF of 18 and 30?
By dividing both numbers by the GCF to check if the quotients are integers.
Can the GCF of 18 and 30 be one of the numbers?
Yes, if one number is a multiple of the other. For 18 and 30, the GCF is 6.
What are the common factors of 18 and 30?
The common factors of 18 and 30 are 1, 2, 3, and 6.
Share :
Practice Test
Which number is a common factor of both 18 and 30?
4
5
6
7
of 10
What is the number of factors of the GCF of 18 and 30?
2
3
4
6
of 10
Which of these numbers is the greatest common factor of 18 and 30?
2
6
3
15
of 10
What is the smallest prime factor of the GCF of 18 and 30?
2
3
5
7
of 10
Which number shares the same GCF as 18 and 30?
20 and 25
24 and 30
18 and 45
18 and 36
of 10
If the GCF of 18 and 30 is added to the number 7, what is the result?
13
14
15
16
of 10
Which of the following numbers is not divisible by the GCF of 18 and 30?
30
36
42
54
of 10
What is the product of the GCF of 18 and 30 and 3?
12
18
24
30
of 10
What is the result when the GCF of 18 and 30 is divided by 2?
2
3
6
9
of 10