What is the GCF of 8 and 20?
2
4
8
10


The greatest common factor (GCF) of 8 and 20 is 4. This result can be derived using several methods, including prime factorization, listing common factors, or applying the Euclidean algorithm. In prime factorization, 8 is expressed as 2³ and 20 as 2²×5 The common factor here is 2, and the lowest power is 2², leading to a GCF of 4. Listing the factors of 8 (1, 2, 4, 8) and 20 (1, 2, 4, 5, 10, 20) also shows that the highest shared factor is 4. The Euclidean algorithm, using successive division, will confirm that 4 is indeed the largest number that divides both 8 and 20 without a remainder, thus demonstrating its role as the GCF of these numbers.
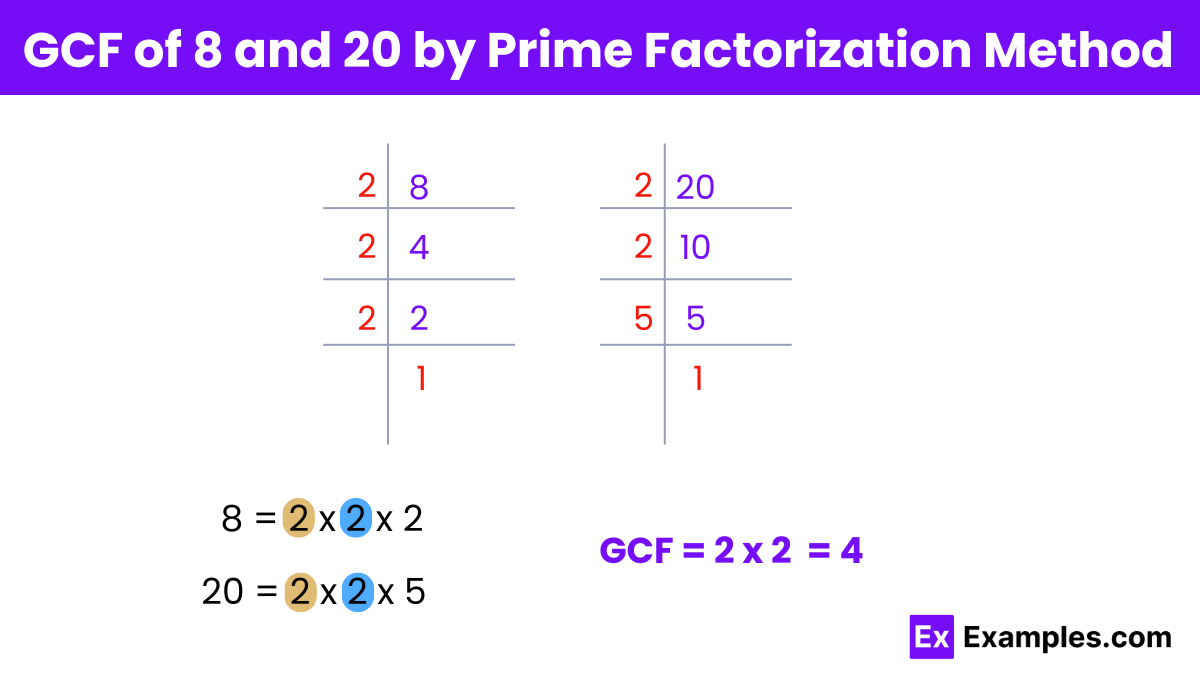
To find the greatest common factor (GCF) of 8 and 20 using the prime factorization method, follow these steps:
Step 1: Prime factorize both numbers:
For 8: 8 = 2³
For 20: 20 = 2² × 5
Step 2: Identify the common prime factors and their lowest powers:
The common prime factor between 8 and 20 is 2. The lowest power of 2 that appears in both factorizations is 2².
Step 3: Multiply the common prime factors with their lowest powers to determine the GCF:
GCF = 2² = 4
Therefore, the greatest common factor (GCF) of 8 and 20 by the prime factorization method is 4.

To find the greatest common factor (GCF) of 8 and 20 using the long division method:
Step 1: Start by dividing the larger number (20) by the smaller number (8).
20 ÷ 8 = 2 with a remainder of 4.
Step 2: Then, take the divisor (8) and divide it by the remainder (4).
8 ÷ 4 = 2 with a remainder of 0.
Since the remainder is now 0, the division process stops here.
Step 3: The divisors at this step where the remainder becomes zero is the greatest common factor (GCF).
GCF = 4.
Therefore, the greatest common factor (GCF) of 8 and 20 by the long division method is 4.

To find the greatest common factor (GCF) of 8 and 20 by listing common factors:
Step 1: List the factors of each number.
Factors of 8: 1, 2, 4, 8
Factors of 20: 1, 2, 4, 5, 10, 20
Step 2: Identify the common factors.
Common factors: 1, 2, 4
Step 3: Determine the greatest common factor.
GCF = 4.
Therefore, the greatest common factor (GCF) of 8 and 20 by listing common factors is 4.
Is there a way to visually represent the GCF of 8 and 20?
Problems involving dividing or sharing quantities in ratios, simplifying algebraic fractions, and more.
It aids in simplifying expressions and solving problems involving ratios and proportions.
Listing common factors might be the quickest for small numbers like these.
Long division and listing common factors are also effective methods.
You can calculate the GCF using methods like prime factorization, listing common factors, or long division.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the GCF of 8 and 20?
2
4
8
10
Which number is a common factor of both 8 and 20?
3
5
6
4
What is the smallest prime factor of the GCF of 8 and 20?
2
3
5
7
What is the sum of the GCF of 8 and 20 and the number 5?
7
9
11
13
If you subtract the GCF of 8 and 20 from 20, what is the result?
12
14
16
18
2
3
5
7
Which pair of numbers has the same GCF as 8 and 20?
12 and 16
6 and 10
4 and 8
15 and 25
Which of the following numbers is not divisible by the GCF of 8 and 20?
12
16
20
24
What is the GCF of 8 and 20 when divided by 4?
1
2
3
4
What is the difference between the GCF of 8 and 20 and the number 2?
1
2
3
4
Before you leave, take our quick quiz to enhance your learning!

