GCF of 9 and 12
GCF of 9 and 12
The simplest way to find the greatest common factor (GCF) of 9 and 12 is by listing their factors and identifying the largest numbers common to both lists. The factors of 9 are 1, 3, and 9, while the factors of 12 are 1, 2, 3, 4, 6, and 12. The common factors shared by both numbers are 1 and 3, with 3 being the largest. Therefore, the GCF of 9 and 12 is 3. This method is direct and effective, especially for smaller numbers, allowing for a quick and clear determination of the greatest common divisor.
GCF of 9 and 12
GCF of 9 and 12 is 3.
GCF of 9 and 12 by Prime Factorization Method.
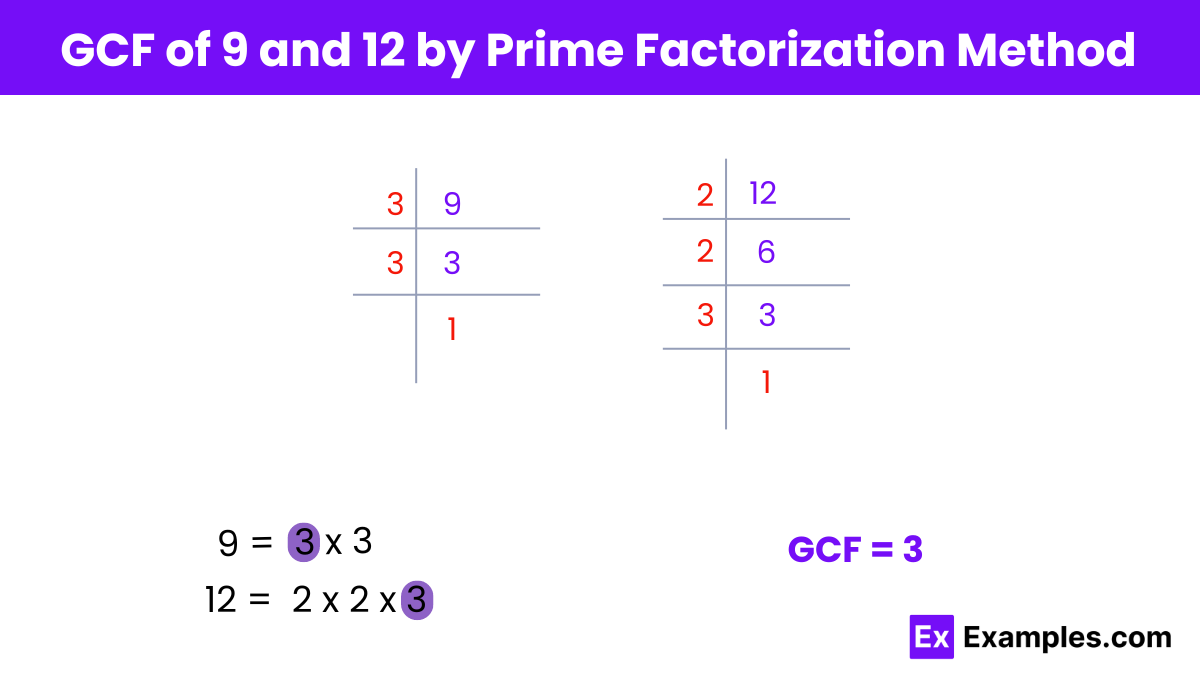
To find the greatest common factor (GCF) of 9 and 12 using the prime factorization method:
Step 1: Prime factorize both numbers:
For 9: 9 = 3²
For 12: 12 = 2² × 3
Step 2: Identify the common prime factors and their lowest powers:
The common prime factor between 9 and 12 is 3. The lowest power of 3 in both factorizations is 3¹.
Step 3: Multiply the common prime factors with their lowest powers to determine the GCF:
GCF = 3¹ = 3
Therefore, the greatest common factor (GCF) of 9 and 12 by prime factorization method is 3.
GCF of 9 and 12 by Long Division Method.
To find the greatest common factor (GCF) of 9 and 12 using the long division method, follow these steps:
Step 1: Start by dividing the larger number (12) by the smaller number (9).
12 ÷ 9 = 1 with a remainder of 3.
Step 2: Then, take the divisor (9) and divide it by the remainder (3).
9 ÷ 3 = 3 with a remainder of 0.
Since the remainder is now 0, the division process stops here.
Step 3: The divisors at this step where the remainder becomes zero is the greatest common factor (GCF).
GCF = 3.
Therefore, the greatest common factor (GCF) of 9 and 12 by the long division method is 3.
GCF of 9 and 12 by Listing Common Factors.
To find the greatest common factor (GCF) of 9 and 12 by listing common factors:
Step 1: List the factors of each number.
Factors of 9: 1, 3, 9
Factors of 12: 1, 2, 3, 4, 6, 12
Step 2: Identify the common factors.
- Common factors: 1, 3
Step 3: Determine the greatest common factor.
The highest number in the list of common factors is 3.
How does understanding GCF benefit everyday decisions?
It aids in making decisions involving ratios, such as splitting ingredients or dividing tasks equally.
Why might someone confuse the GCF with the LCM?
Because both involve finding commonalities between sets of numbers, though they serve different mathematical purposes.
What if the GCF of 9 and 12 was wrongly calculated as 4?
This would be incorrect as 4 is not a factor of 9.
What is the method to find the GCF using subtraction?
Continually subtract the smaller number from the larger until the numbers equal each other, revealing the GCF.
Is there a quick method to find the GCF of small numbers like 9 and 12?
Listing common factors is typically the quickest method for small numbers.
How many common factors do 9 and 12 have?
They have two common factors: 1 and 3.
Share :
