Integration

What is Integration?

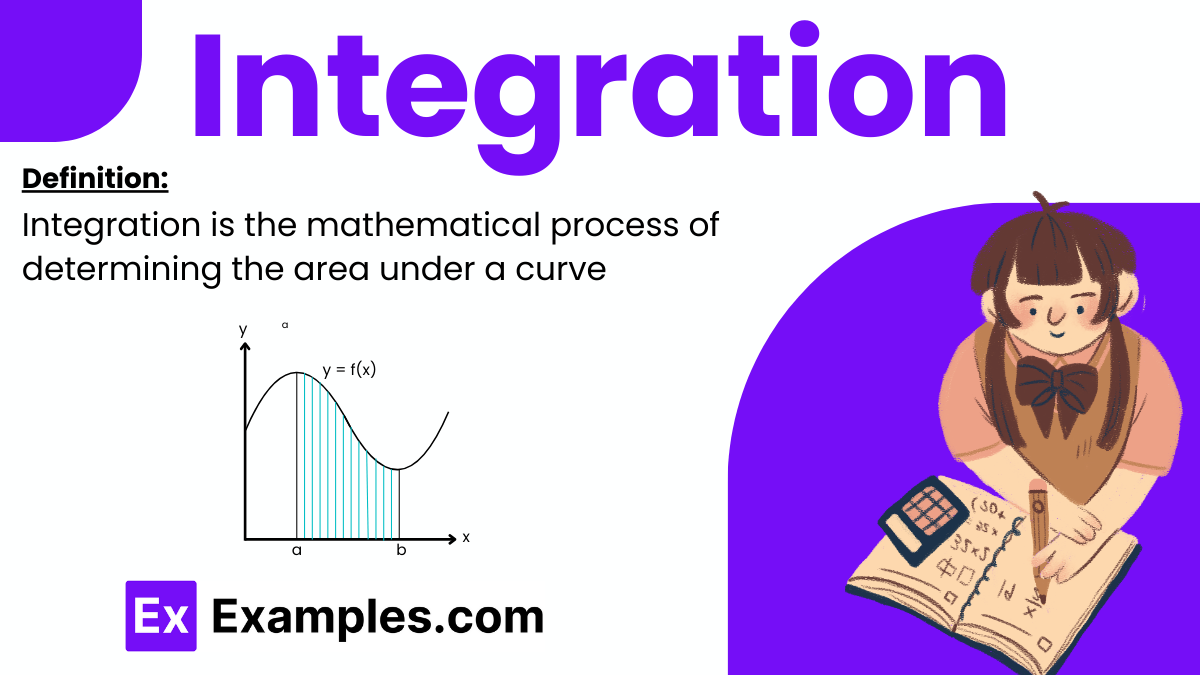
Integration is a fundamental concept in mathematics, particularly within the field of calculus. It represents the process of calculating the area under a curve described by a mathematical function, enabling a deeper understanding of the space and the changes within that space. Integration allows us to sum up parts to find the whole, which is particularly useful in various scientific and engineering applications.

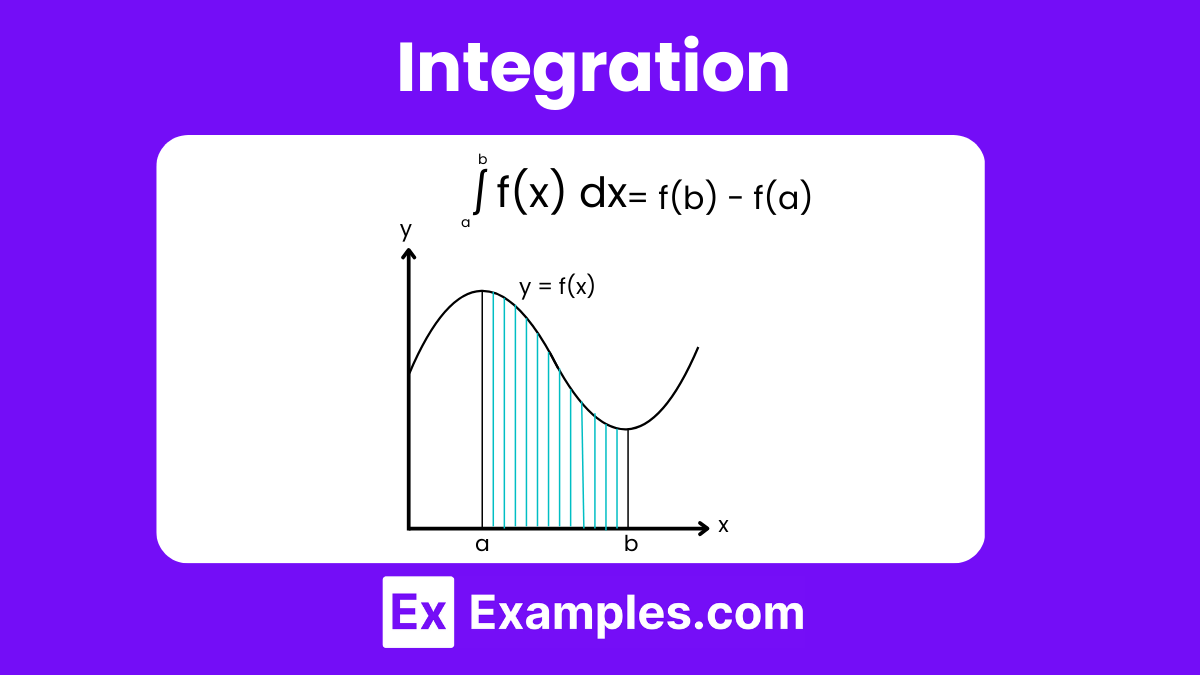
Integration is the mathematical process of determining the area under a curve. This involves approximating the area by summing the areas of numerous small rectangles beneath the curve, with the total becoming increasingly accurate as more rectangles are used. This sum approaches a precise value, known as the integral of the function, which represents the area under the curve within specified limits. Integration is also described as finding the antiderivative of a function, meaning it determines a function whose derivative is the original function. When a function is integrable and its integral over a specified domain is finite, this results in what is known as definite integration.

If d/dx(F(x) = f(x), then ∫ f(x) dx = F(x) +C. These are indefinite integrals. For example, let f(x) = x⁴ be a function. The derivative of f(x) is f’(x) = 3x^² and the antiderivative of 3x^² is f(x) = x³

Function F(x)	Derivative F'(x) = f(x)	Antiderivative of f(x)
x³ + 0	3x²	x³ + ?
x³ + 2	3x²	x³ + ?
x³ – 4	3x²	x³ + ?

Rules of Integration

We are familiar with the derivative formulas for key functions, which directly inform their corresponding standard integrals. Below are a few important integration formulas derived from these well-known derivative relationships.

Sum and Difference Rules:

• ∫ [f(x)+g(x)] dx = ∫ f(x) dx + ∫ g(x) dx
• ∫ [f(x)-g(x)] dx =∫ f(x) dx – ∫ g(x) dx

Power Rule: ∫ x^ⁿ dx = (x^ⁿ⁺¹)/ (n+1)+ C. (Where n ≠ -1)

Exponential Rules:

• ∫ eˣ dx = eˣ+ C
• ∫ aˣ dx = aˣ/ln(a) + C
• ∫ ln(x) dx = x ln(x) -x + C

Constant Multiplication Rule:

• ∫ a dx = ax + C, where a is the constant.

Reciprocal Rule:

• ∫ (1/x) dx = ln(x)+ C

Properties of Integration

A few properties of indefinite integrals are:

• ∫ [f(x)±g(x)] dx =∫ f(x) dx ± ∫ g(x) dx
• ∫ k f(x) dx = k ∫ f(x) dx, where k is any real number.
• ∫ f(x) dx = ∫ g(x) dx, if ∫ [f(x)-g(x)] dx = 0
• The combination of first two properties arise to∫[k₁f₁(x)dx+k2₂f₂(x)dx+………knf(x)dx]=k₁∫f₁(x)dx+k₂∫f₂(x)dx+….+kn∫f(x)dx

Methods of Integration

Integration is a fundamental concept in calculus used to compute areas under curves, volumes, and other quantities that aggregate infinitesimal data points. Here are some key methods of integration used in mathematics:

1. Substitution Method

This method involves changing the variable of integration to simplify the integral. It’s particularly useful when dealing with composite functions or integrals involving trigonometric identities. The substitution is usually chosen to make the integral look simpler or more standard.

2. Integration by Parts

Based on the product rule for differentiation, integration by parts is used when integrating the product of two functions. It is often applied when one function is easily integrable and the other is easily differentiable.

3. Partial Fractions

When integrating rational functions, where the numerator and denominator are polynomials, the partial fractions method is useful. This approach involves decomposing a complex fraction into simpler fractions that are easier to integrate.

4. Trigonometric Integration

This involves integrating functions that contain trigonometric expressions. Techniques like using trigonometric identities to simplify the integrals or converting products of sine and cosine into sums or differences are common.

5. Trigonometric Substitution

Used for integrals containing square roots of expressions like 𝑎²−𝑥², 𝑎²+𝑥², or 𝑥²−𝑎². Trigonometric substitution simplifies these types of integrals into standard trigonometric integrals by substituting a trigonometric function for 𝑥.

6. Improper Integrals

These are used when the limits of the integral are infinite or the integrand has an infinite discontinuity within the limits of integration. Such integrals are handled by defining them as limits of proper integrals as the interval grows infinitely large or approaches the point of discontinuity.

7. Numerical Integration

When an integral cannot be solved analytically, numerical methods such as the Trapezoidal Rule, Simpson’s Rule, or Monte Carlo integration are used to approximate the value of the integral.

Integral Calculus

Integral calculus is a branch of calculus that deals with the concept of integration, an essential mathematical operation used to determine the accumulation of quantities and the areas under and between curves. Here’s a detailed look at integral calculus:

Concept of Integration

Integration is the inverse process of differentiation. While differentiation focuses on rates of change and slopes of curves, integration deals with the accumulation of quantities, such as areas under curves, volumes of solids, and other related sums over intervals.

Two Main Types of Integrals

1. Indefinite Integrals: These represent the general form of antiderivatives. An indefinite integral of a function 𝑓(𝑥) is given by ∫𝑓(𝑥) 𝑑𝑥 and includes an arbitrary constant 𝐶, since differentiation of a constant is zero. It gives a family of functions whose derivative is the integrand.
2. Definite Integrals: These calculate the net accumulation of a function between two points, providing a specific numerical value. The definite integral of 𝑓(𝑥) from 𝑎a to 𝑏b is denoted as ∫𝑎𝑏𝑓(𝑥) 𝑑𝑥, which can be interpreted as the signed area under the curve of 𝑓(𝑥) from 𝑥=𝑎 to 𝑥=𝑏.

Fundamental Theorem of Calculus

This theorem bridges the concepts of differentiation and integration, stating that:

• The first part establishes the connection between indefinite integrals and antiderivatives.
• The second part allows the evaluation of definite integrals via antiderivatives, specifying that if 𝐹 is an antiderivative of f, then ∫ₐᵇ𝑓(𝑥) 𝑑𝑥=𝐹(𝑏)−𝐹(𝑎).

Methods of Integration

Several techniques are employed to perform integrations, particularly when functions are complex:

• Substitution: Useful when a change of variable can simplify the integral.
• Integration by Parts: Applies to products of functions and is based on the product rule for differentiation.
• Partial Fractions: Decomposes complex rational functions into simpler fractions that are easier to integrate.
• Trigonometric Substitution: Useful for integrals involving square roots of quadratic expressions.
• Numerical Integration: Techniques like the Trapezoidal Rule and Simpson’s Rule are used when integrals cannot be solved analytically.

Integration – Inverse Process of Differentiation

Integration is fundamentally the inverse process of differentiation in calculus. While differentiation focuses on finding the rate at which one quantity changes with respect to another, integration involves accumulating the quantities to determine the total effect of these changes over a period or along a continuum.

Understanding the Relationship

Differentiation and integration are two core operations in calculus, often referred to as the fundamental theorems of calculus. Here’s how they connect:

• Differentiation: Determines the derivative, representing the rate of change of a function. For example, differentiating the position function with respect to time gives the velocity function.
• Integration: Calculates the integral, summing these instantaneous rates of change to reconstruct the original function or to determine the total accumulation. For instance, integrating the velocity function over time yields the displacement.

Applications of Integration

Integration serves a variety of purposes across different fields:

• Area Calculation: It can calculate the area under curves and between curves, crucial in physics, engineering, and statistics.
• Volume Determination: By integrating a cross-sectional area, it can determine the volume of irregular shapes.
• Average Value: Integration is used to compute the average value of a function over a given interval, useful in economics and social sciences.

Practical Insights for Integration

To effectively apply integration:

1. Identify the Function: Clearly define the function that needs to be integrated and understand its behavior across the domain.
2. Set Limits of Integration: Determine the appropriate limits for definite integrals, specifying the range over which the integration is to occur.
3. Choose the Right Method: Depending on the complexity of the function, choose the most suitable method of integration, such as substitution, integration by parts, or numerical integration techniques.
4. Use Technological Tools: For more complex functions, consider using computational tools or software designed for symbolic calculation, which can simplify the process of integration.