Angles

What are Angles?

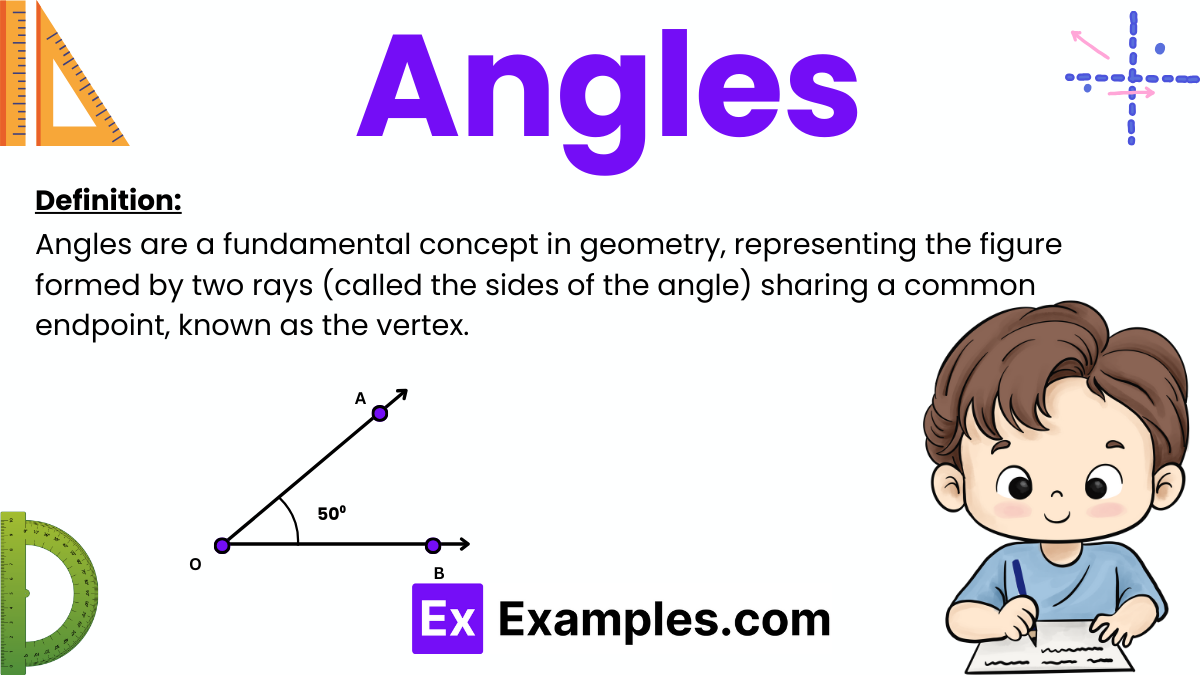
Angles are a fundamental concept in geometry, representing the figure formed by two rays (called the sides of the angle) sharing a common endpoint, known as the vertex. They are typically measured in degrees or radians and describe the amount of turn between each arm. Angles are used to describe the shape, size, and direction of corners found throughout daily life and various fields such as mathematics, engineering, and architecture.

Parts of an Angle

An angle primarily consists of two essential parts:

Arms: These are the two rays that extend from a common point and form the angle. The arms can be of any length and direction but share the vertex as their starting point.

Vertex: This is the specific point at which the two arms meet. It acts as the pivotal point from which the angle is measured.

Measure of an angle

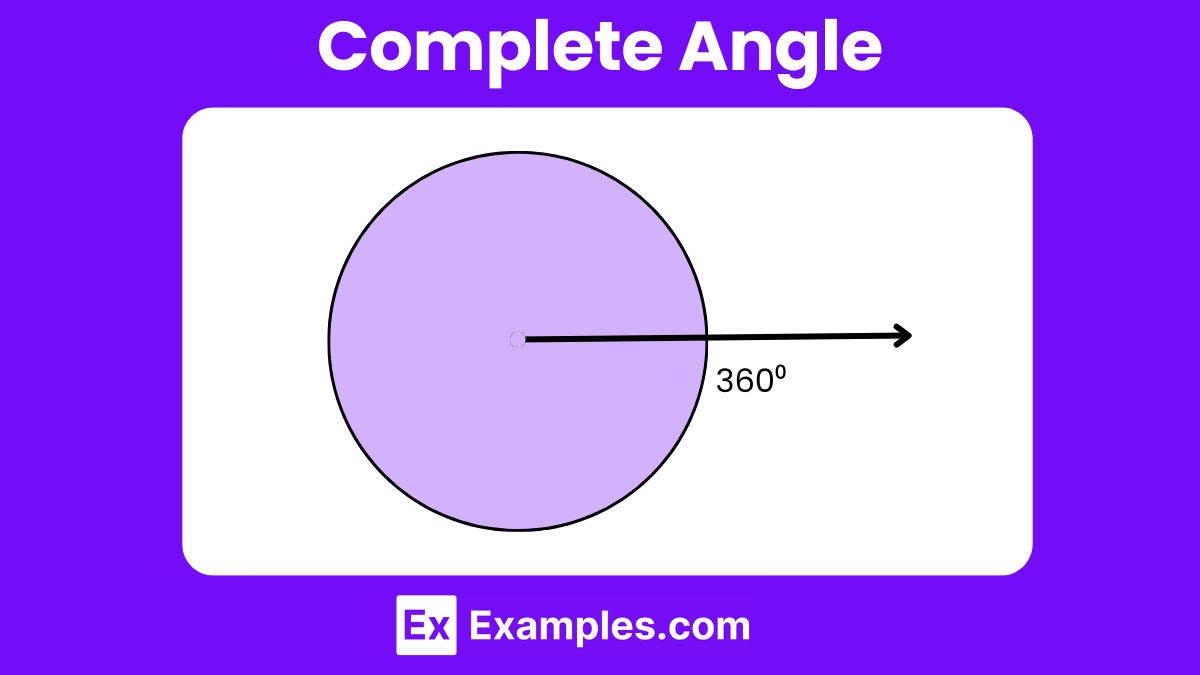
An angle is measured in degree, with a full rotation around a point forming a complete angle of 360°.

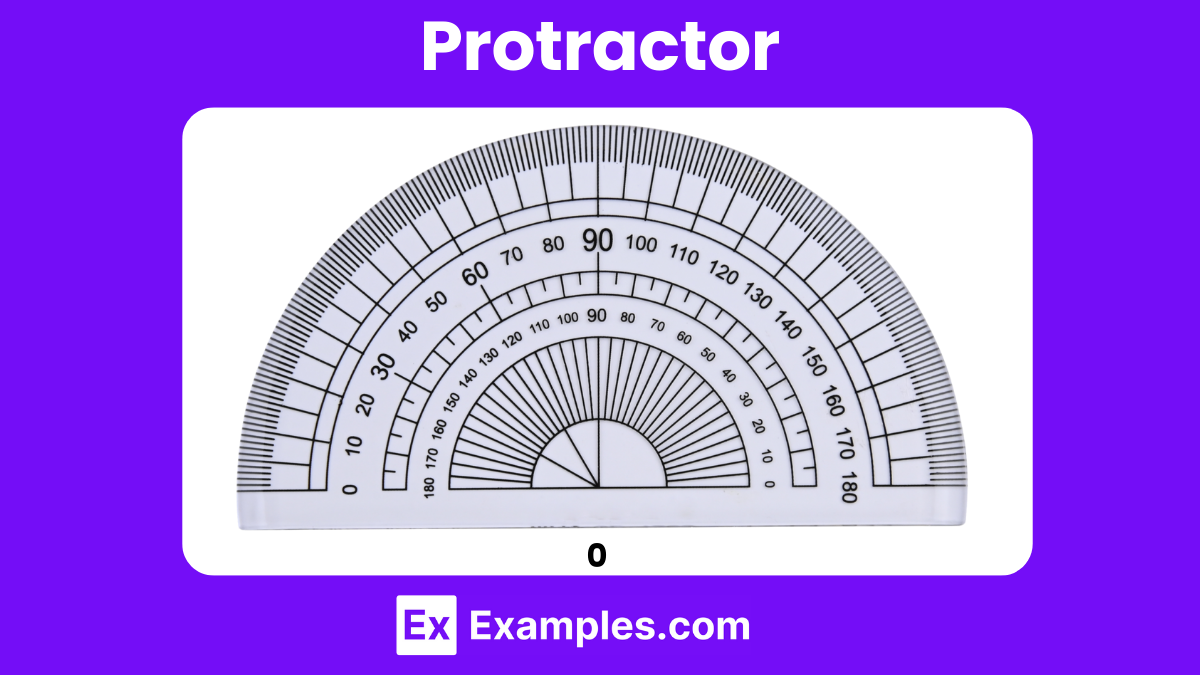
The most effective tool for measuring an angle is a protractor, which is typically a semi-circular, translucent instrument. It facilitates precise measurement of angles in degrees. A protractor is marked with degrees from 0° to 180° on both the outer and inner scales. The outer scale measures degrees clockwise, while the inner scale measures them counterclockwise. This dual scale system allows for easy and accurate reading of both acute and obtuse angles, making the protractor indispensable in geometry and various practical applications.

Types of Angles and their Properties

Angles are categorized based on their measure, which defines their unique characteristics. Let’s explore each type of angle and its properties:

Acute Angle

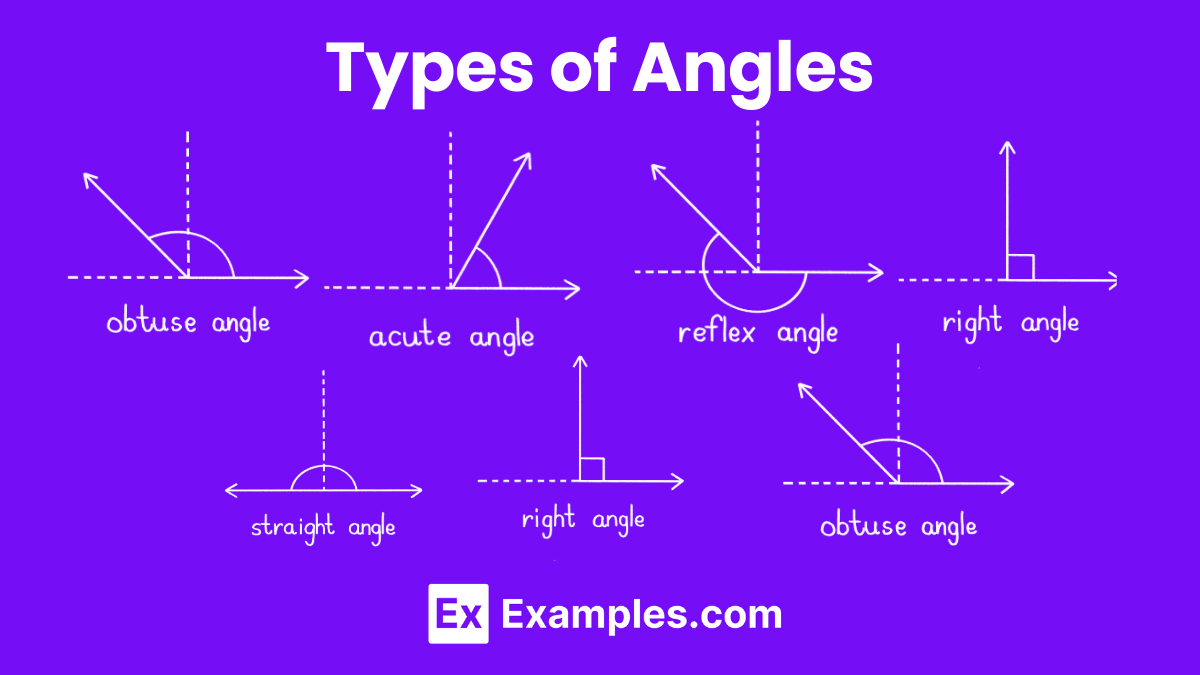
An acute angle measures greater than 0° but less than 90°. These angles are sharp and are often seen in various geometric figures.

Right Angle

A right angle measures exactly 90°, resembling the shape of the letter L. This type of angle is prevalent in everyday objects and represents a quarter turn.

Obtuse Angle

An obtuse angle is one that measures more than 90° but less than 180°. These angles appear wider and are less common than acute angles.

Straight Angle

A straight angle measures exactly 180°, forming a straight line. This angle represents a half turn, consisting of two right angles back-to-back.

Reflex Angle

A reflex angle measures more than 180° but less than 360°. These angles are larger than a straight angle and span more than half a turn.

Complete Angle

A complete angle measures exactly 360°, representing a full rotation around a point.

Angle Measurement Based on Rotation

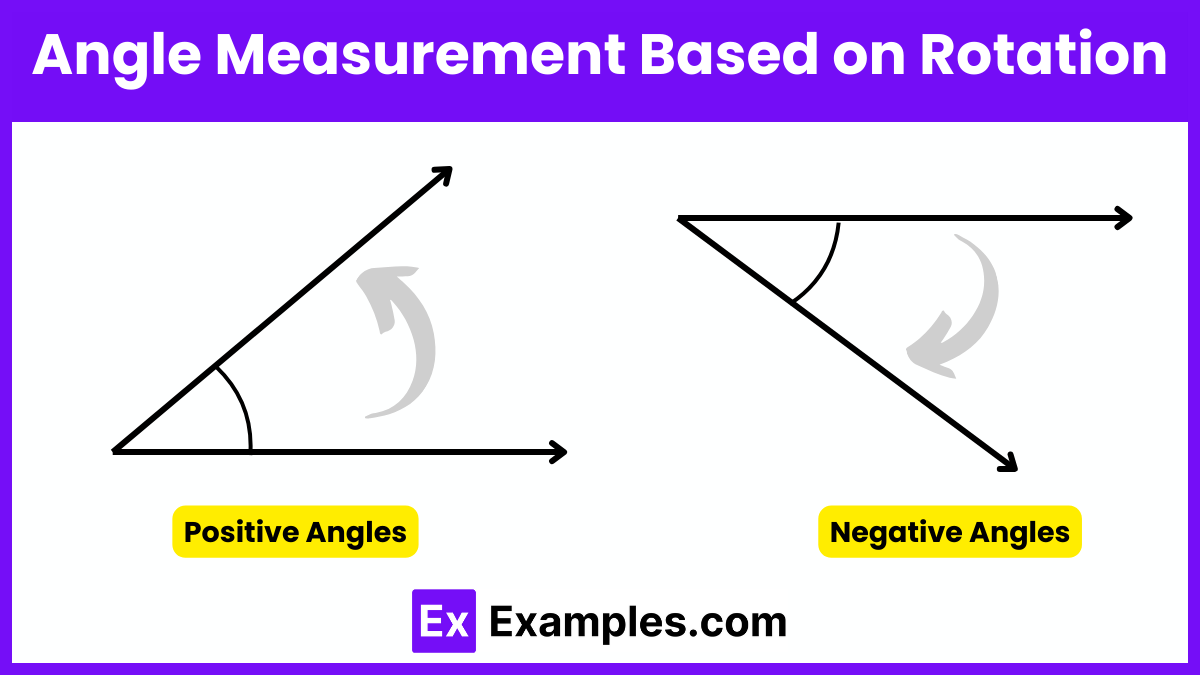
Angles can also be classified based on the direction of their rotation:

Positive Angles

Positive angles are measured in a counterclockwise direction from the base. This is the standard direction for measuring angles in mathematics.

Negative Angles

Negative angles are measured in a clockwise direction from the base. These angles represent a reverse rotation compared to the typical angle measurement.

How to Measure an Angle?

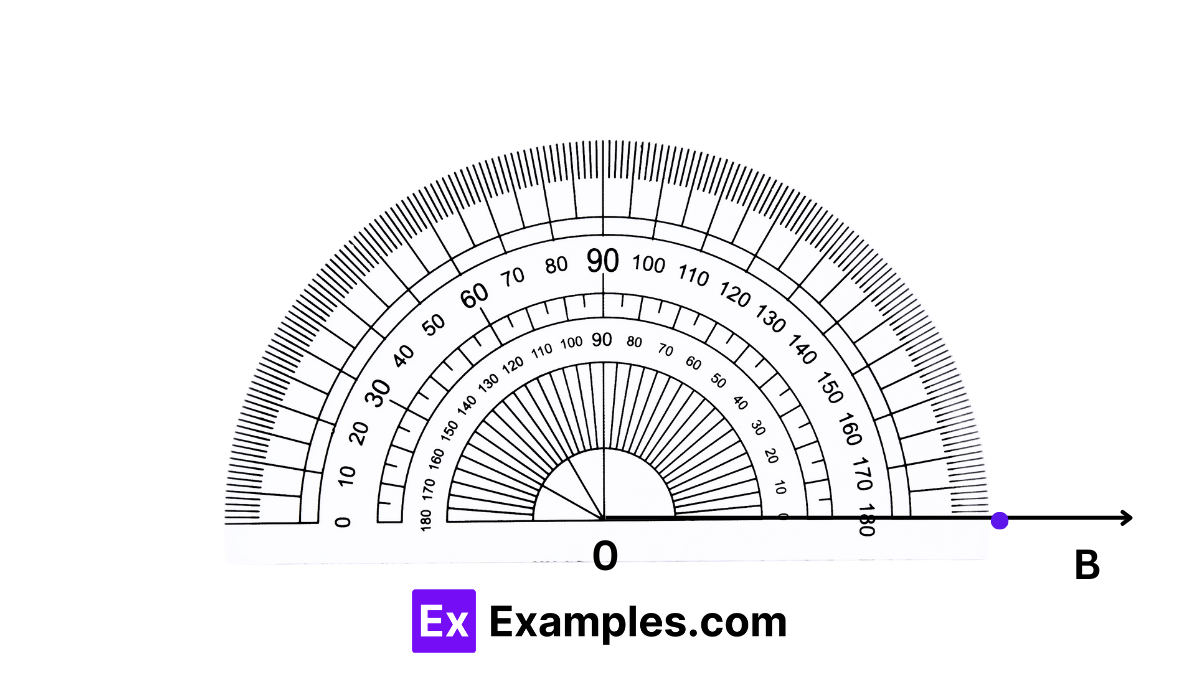
We use protractors to accurately measure angles. Consider the angle ∠AOB depicted in the figure below. At first glance, ∠AOB appears to be an acute angle, indicating that its measurement is greater than 0° and less than 90°. Let’s explore how to measure this angle using a protractor effectively.

How to Measure an Acute Angle?

Let us try to measure the given ∠AOB.

Step 1: Position the protractor so that the ray OB aligns with the baseline of the protractor. Begin by observing the inner scale, starting from the 0° mark located at the bottom right of the protractor. This alignment ensures accurate measurement of the angle.

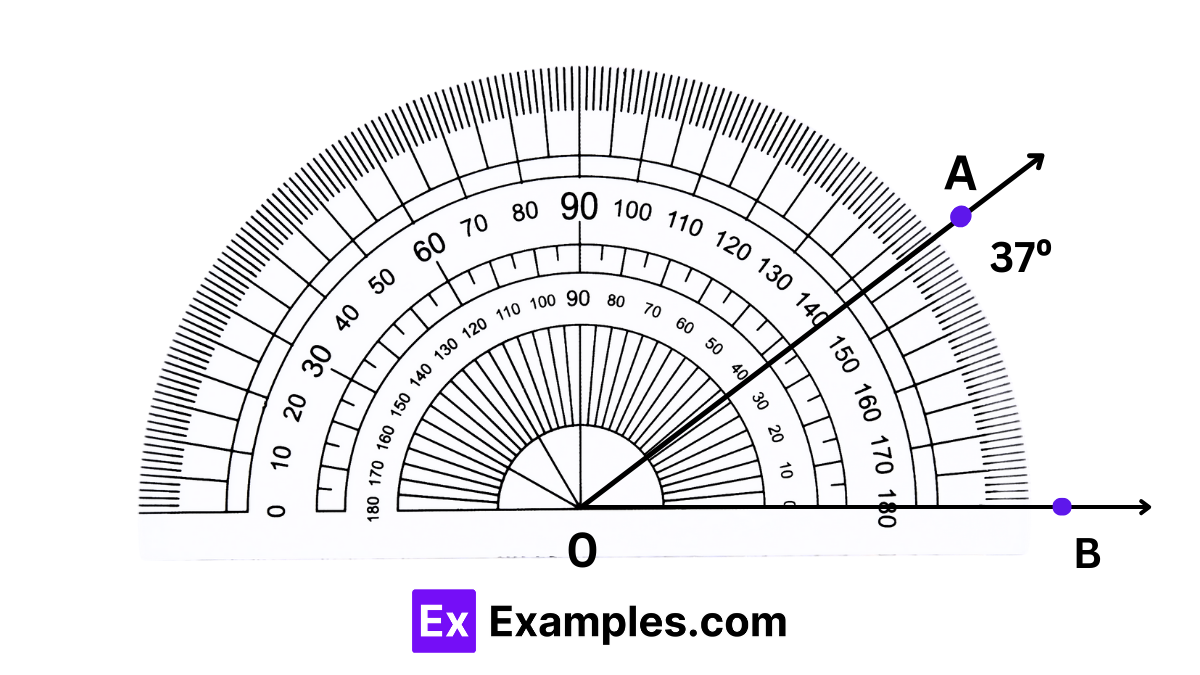
Step 2: Identify the number on the protractor that aligns with the second ray to determine the angle’s measurement. Use the protractor’s inner scale for this measurement. Consequently, the angle ∠AOB measures 37°.

How to Measure an Obtuse Angle?

Now, let us try to measure the given ∠AOC.

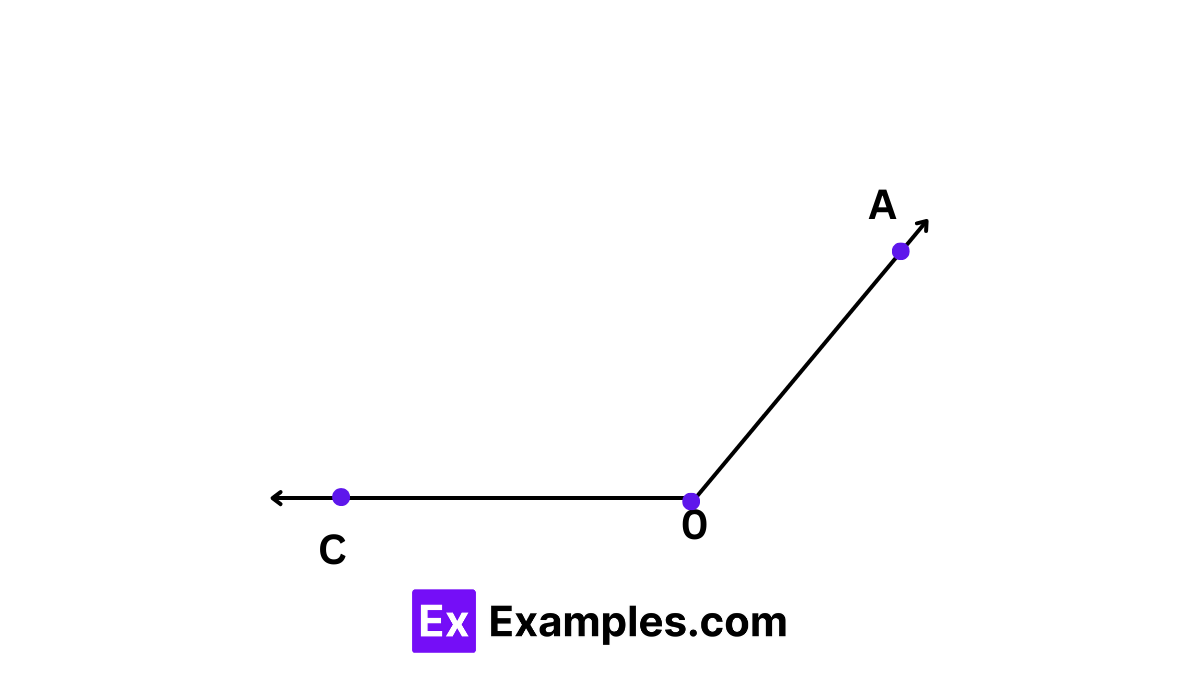
Step 1: To measure the angle, use the outer scale of the protractor, starting from the 0° mark located at the bottom left.

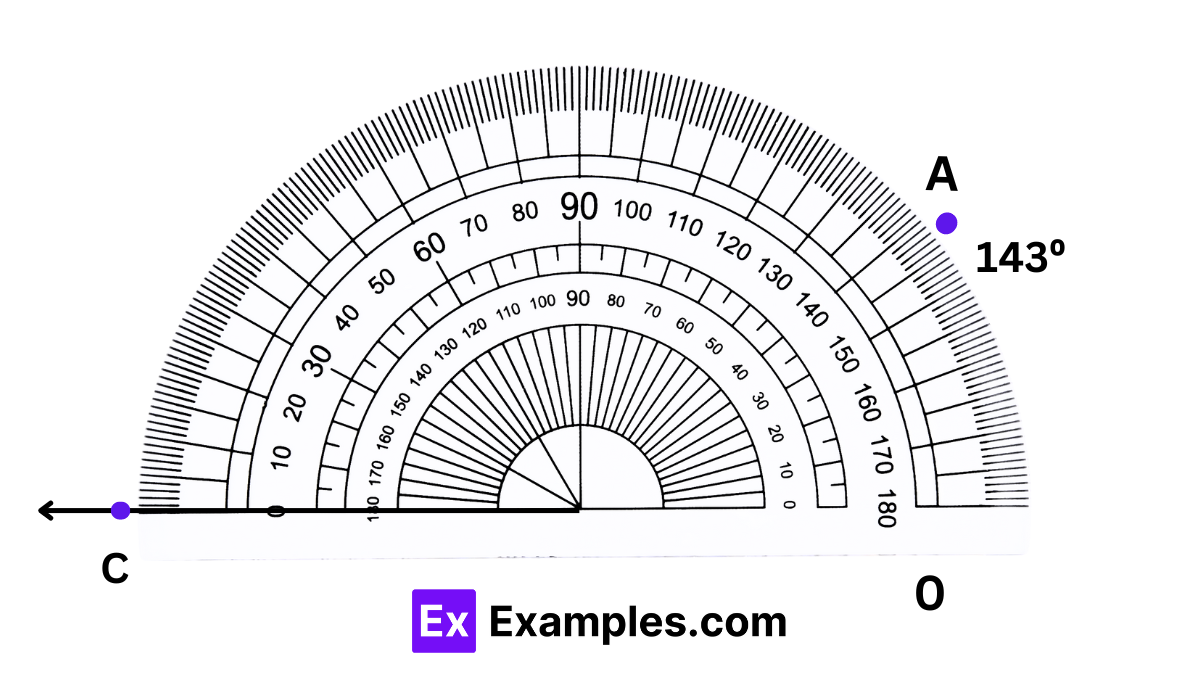
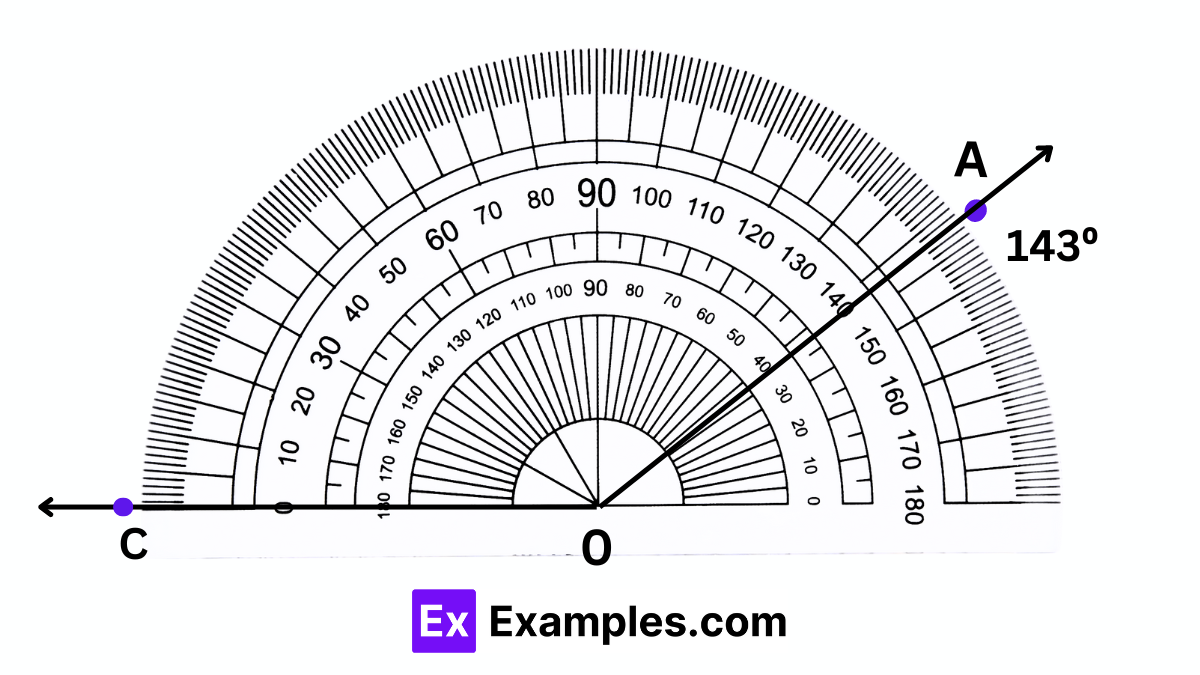
Step 2: The number on the outer scale of the protractor that aligns with ray OA indicates the measurement of ∠AOC. Therefore, ∠AOC measures 143°.

How to Construct Angles?

Constructing angles accurately is essential in various fields such as drafting, architecture, and even school projects. Here’s a step-by-step guide on how to draw a 50° angle using a protractor:

Step 1: First, draw a straight line, labeling it as ray OB. Position the protractor so that its baseline aligns perfectly with ray OB, ensuring the center point of the protractor is at the endpoint of the ray, typically marked as O.

Step 2: Using the inner scale of the protractor, mark a point A above the marking on the protractor that corresponds to 50°.

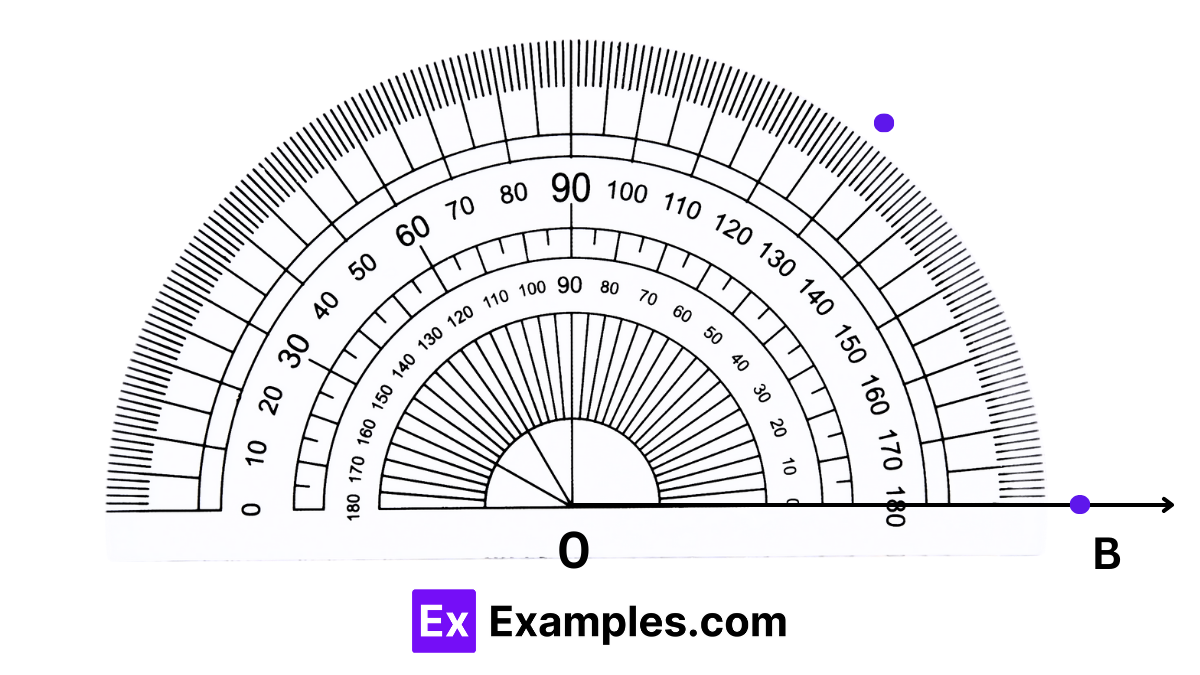
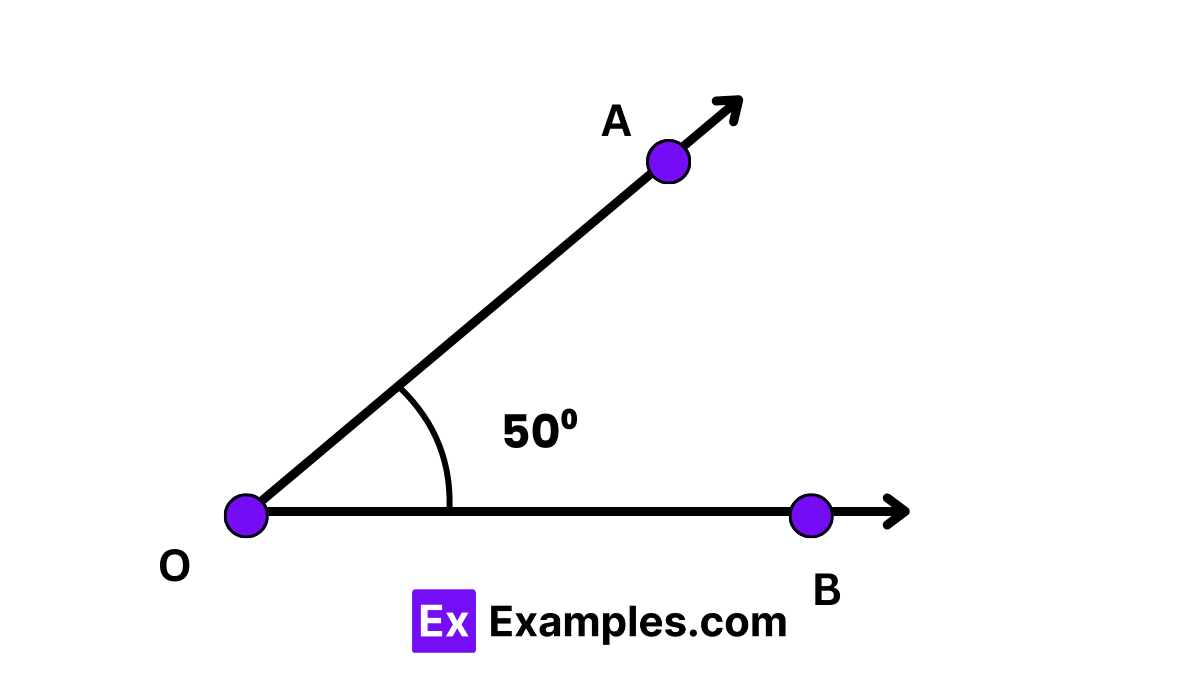
Step 3: After removing the protractor, draw a ray starting at point O and extending through point A. This creates the desired angle, ∠AOB, which measures 50°.

Important Notes on Angles

Here are some crucial points to understand about angles, which are essential for grasping their properties and applications in geometry:

1. Acute Angle: An angle that measures greater than 0° and less than 90°. These angles are smaller than a right angle and commonly found in various geometric shapes.
2. Right Angle: Exactly measures 90° and is often represented by the corner of a square or rectangle. This angle forms the shape of the letter L and is a fundamental aspect of perpendicular lines.
3. Obtuse Angle: An angle that is greater than 90° but less than 180°. These angles are larger than a right angle and appear more ‘spread out.’
4. Straight Angle: Exactly measures 180°, appearing as a straight line. This angle signifies a half-turn and is equivalent to two right angles put together.
5. Reflex Angle: An angle that measures greater than 180° but less than 360°. These angles extend more than a straight angle but less than a complete rotation.
6. Complete Angle: Measures exactly 360°, representing a full rotation around a point. This is also known as a perigon angle.
7. Complementary Angles: Two angles whose sum equals 90°. These are typically acute angles that pair up to form a right angle.
8. Supplementary Angles: Two angles whose measures add up to 180°. These can be two right angles or any combination of angles that reach a straight angle when added together.
9. Adjacent Angles: Two angles that share a common vertex and side but do not overlap. These angles are next to each other and often appear in geometric constructions.
10. Vertical Angles: Also known as opposite angles, these are equal angles formed by two intersecting lines. Vertical angles are always congruent.

Practice Problems On Angles

Problem 1: Identifying Angles

Draw the following angles and identify them as acute, obtuse, right, straight, reflex, or complete:

1. An angle of 25°
2. An angle of 90°
3. An angle of 175°
4. An angle of 270°
5. An angle of 360°

Problem 2: Measuring and Drawing Angles

Using a protractor, measure and draw the following angles:

1. Draw an acute angle of 45°.
2. Draw a right angle.
3. Draw an obtuse angle of 120°.
4. Draw a straight angle.
5. Draw a reflex angle of 300°.

Problem 3: Angle Calculation

Calculate the missing angle in each scenario:

1. Two angles in a triangle measure 65° and 35°. What is the measure of the third angle?
2. If two angles on a straight line add up to 180° and one angle is 110°, what is the measure of the other angle?
3. An angle is three times the size of its complement. What are the measures of the two angles?

Problem 4: Real-Life Application

Identify the type of angle formed in the following real-life situations:

1. The angle between the hands of a clock at 3:00.
2. The angle formed by the open lid of a laptop partially closed at about halfway.
3. The angle formed by a slice of pizza cut with a straight line from the tip to the crust edge.

Problem 5: Creating Complex Figures

Create a diagram that includes the following:

1. Two acute angles that are complementary.
2. One obtuse angle adjacent to a right angle.
3. A reflex angle paired with an acute angle in a scenario of your choice.

Solved Examples On Angles

Example 1: Identifying Angle Types

Question: Identify the type of each angle:

• An angle of 30°
• An angle of 95°
• An angle of 180°
• An angle of 270°

Solution:

• 30° is an acute angle because it is less than 90°.
• 95° is an obtuse angle because it is greater than 90° but less than 180°.
• 180° is a straight angle because it is exactly 180°.
• 270° is a reflex angle because it is greater than 180° but less than 360°.

Example 2: Calculating Missing Angle in a Triangle

Question: A triangle has two angles measuring 45° and 70°. What is the measure of the third angle?

Solution: The sum of the angles in a triangle is always 180°. Therefore: Third Angle=180°−(45°+70°)=180°−115°=65°Third Angle=180°−(45°+70°)=180°−115°=65° The third angle measures 65°.

Example 3: Complementary and Supplementary Angles

Question: If one angle measures 65°, find its complementary and supplementary angles.

Solution:

• Complementary angle: 90°−65°=25°90°−65°=25° The complementary angle is 25°.
• Supplementary angle: 180°−65°=115°180°−65°=115° The supplementary angle is 115°.

Example 4: Using Vertical Angles

Question: Two intersecting lines form four angles. If one of the angles is 110°, what are the measures of the other three angles?

Solution:

• The angle opposite the 110° angle is also 110° (vertical angles are equal).
• The angles adjacent to the 110° angles must add up to 180° since they are supplementary. 180°−110°=70°180°−110°=70°
• Therefore, the other two angles are each 70°.

FAQs