What is the square of 1296?
1,679,616
1,777,216
1,681,856
1,782,576
of 10
Square & Square Root of 1296 – Examples, Methods, Calculation
Square & Square Root of 1296 – Examples, Methods, Calculation
In the domain of mathematics, particularly within algebraic studies, squares and square roots are pivotal. Squaring a number, such as 1296, involves multiplying it by itself to yield a result like 1679616, constituting a foundational operation. This operation is essential for exploring the properties of rational numbers (expressible as a fraction) and irrational numbers (not expressible as a neat fraction). Understanding these fundamental concepts enriches comprehension of mathematical relationships and patterns, elucidating the interplay between algebraic expressions and numerical values.
Square of 1296
1296² (1296 × 1296) = 1679616
A square number, exemplified by the square of 1296, results from multiplying a number by itself. In this case, squaring 1296 yields 1679616. Square numbers, fundamental in mathematics, serve as building blocks for exploring algebraic relationships and understanding numerical patterns.
Square Root of 1296
√1296 = 36
The square root of 1296, denoted as √1296, equals 36. This represents the number which, when multiplied by itself, yields 1296. Understanding square roots is crucial in algebra, as it enables finding the side length of a square with a given area, contributing to solving various mathematical problems.
Square Root of 1296: 36
Exponential Form: 1296^½ or 1296^0.5
Radical Form: √1296
Is the Square Root of 1296 Rational or Irrational?
The square root of 1296 is a rational number
The square root of 1296 is rational because it equals 36, a whole number. Rational numbers can be expressed as a fraction of two integers, which is the case here. Unlike irrational numbers, rational numbers terminate or repeat in their decimal representations.
Rational number : A rational number can be expressed as a fraction a/b, where both a and b are integers and the denominator isn’t zero.
Examples include positive, negative, or zero values like 3/4, -5/2, 0, 1, -2, etc.
Irrational number : An irrational number, such as √2 or π, cannot be expressed as a fraction of two integers. Its decimal expansion neither ends nor repeats, thus defying representation in the form a/b.
For example, √2 has a non-repeating, non-terminating decimal expansion (√2 ≈ 1.41421356…).
Method to Find Value of Root 1296
To find the square root of 1296, you can use various methods such as:
Prime Factorization Method: Express 1296 as a product of prime factors (2 × 2 × 2 × 2 × 3 × 3 × 3 × 3). Then, pair identical factors and take one from each pair, resulting in 2 × 3 × 3 = 36.
Long Division Method: Estimate the square root, then perform long division to refine the approximation until you achieve the desired level of accuracy.
Calculator or Software: Use a calculator or mathematical software to directly compute the square root of 1296, which is 36.
Regardless of the method chosen, the result will be the same: the square root of 1296 is 36.
Square Root of 1296 by Long Division Method
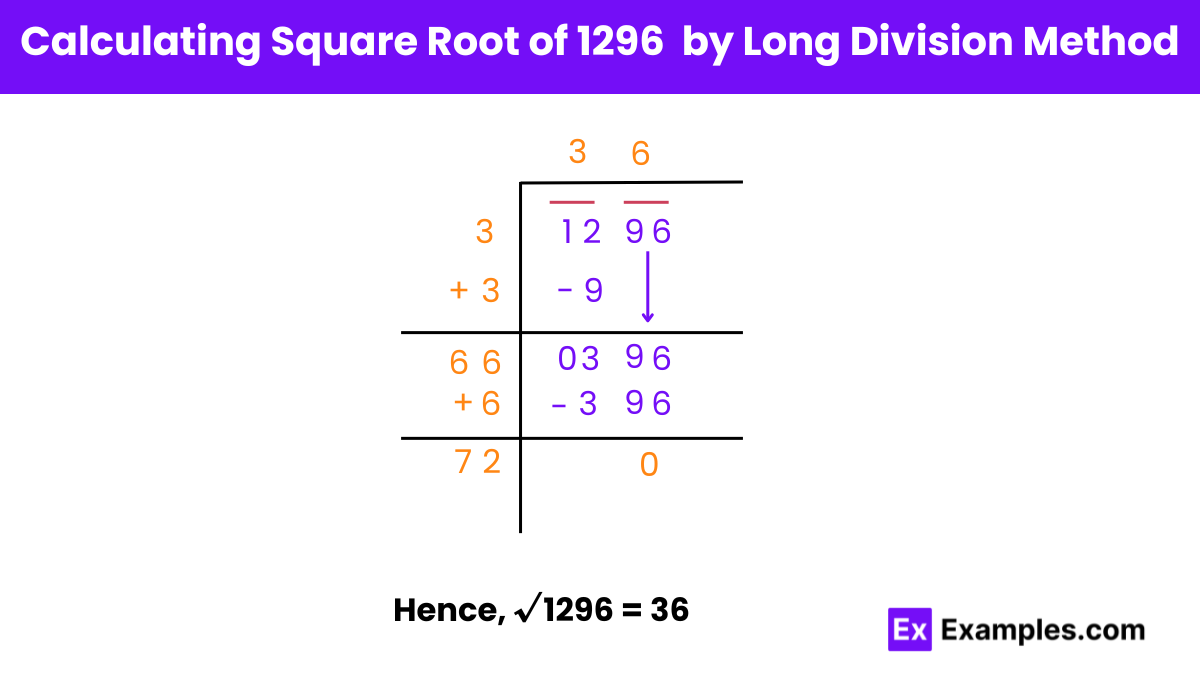
Long Division Method: Finding the Square Root of 1296
1. Grouping Digits:
Start by grouping the digits from the unit’s place in pairs of two by placing a bar on top of them. In the case of 1296, we have two pairs: 12 and 96.
2. Finding Initial Approximation:
Find a number, let’s call it ‘a’, such that a × a is less than or equal to 12. In this case, a will be 3 because 3 × 3 = 9, which is less than 12.
3. Performing Division:
Perform long division to find the quotient and remainder. Then, add the divisor ‘a’ with itself to get the new divisor.
4. Bringing Down Digits:
Bring down the next pair of numbers to form the new dividend. In this case, the new dividend becomes 396.
5. Refining the Approximation:
Find a number ‘n’ such that the product of the current divisor and ‘n’ is less than or equal to the new dividend. Continuously refine the approximation until the desired level of accuracy is achieved.
6. Obtaining the Result:
The square root of 1296, obtained through the long division method, is 36.
1296 is Perfect Square root or Not?
Yes, 1296 is a perfect square number
Yes, 1296 is a perfect square because it can be expressed as the square of an integer. Its square root, √1296, equals 36, which is a whole number. Therefore, 1296 is a perfect square.
FAQS
What is the digital root of 1296?
The digital root of 1296 is calculated by repeatedly adding its digits until a single-digit number is obtained. In this case, 1 + 2 + 9 + 6 = 18, and further, 1 + 8 = 9.
Is 1296 a palindrome number?
No, 1296 is not a palindrome number because it reads differently backward (which would be 6921).
How many factors does 1296 have?
The number 1296 has multiple factors. To find them, you can use methods like prime factorization or division to list all the factors.
Can 1296 be written as the sum of two perfect squares?
Yes, 1296 can be expressed as the sum of two perfect squares: 36^2 (1296) = 34² + 14².
What is the square of 36, the square root of 1296?
The square of 36, the square root of 1296, equals 1296.
Share :
Practice Test
What is the square root of 1296?
24
32
36
48
of 10
What is the value of 36 squared?
1296
1225
1444
1024
of 10
If the square root of a number is 36, what is the original number?
1296
1444
1089
1024
of 10
What is the approximate value of the square root of 1296 if rounded to the nearest integer?
35
36
37
38
of 10
What is the result of squaring the square root of 1296?
1126
1135
1223
1296
of 10
Which of the following numbers is a perfect square?
1136
1296
1376
1420
of 10
What is the square root of 1296 written as a fraction?
72/2
36/1
18/1
64/1
of 10
Which number is not a factor of 1296?
12
15
24
27
of 10
What is the next perfect square after 1296?
1369
1444
1521
1600
of 10