What is the square of 149?
22,201
22,401
22,601
22,801


In the realm of mathematics, particularly within algebraic studies, squares and square roots are pivotal. Squaring a number, exemplified by multiplying 149 by itself to yield 22201, is fundamental. It delves into properties of rational and irrational numbers, enriching comprehension of mathematical relationships and patterns, essential for deeper mathematical understanding.
149²(149 × 149) = 22201
The square number is obtained by multiplying 149 by itself, resulting in the square of 149, which equals 22,201. This mathematical operation showcases the fundamental concept of squaring a number, crucial in algebraic studies and understanding numerical relationships and patterns.
√149 = 12.2065556157
Or
√149 = 12.206 Upto 3 decimals
The square root of 149, approximately 12.207, represents a number whose square equals 149. Understanding this relationship between the square root and the square of 149 is fundamental in mathematics. It exemplifies the inverse operation to squaring, crucial for solving equations and grasping numerical concepts.
Square Root of 149 : 22.627416998
Exponential Form : 149^½ or 149^0.5
Radical Form : √149
The square root of 149 is irrational.
The square root of 149 is an irrational number because it cannot be expressed as a fraction of two integers. Its decimal expansion is non-terminating and non-repeating. Therefore, it falls into the category of irrational numbers.
Rational Number:
A rational number is any number that can be expressed as a fraction, where both the numerator and denominator are integers, and the denominator is not zero. It is typically denoted in the form ( \frac{a}{b} ). Examples include 3/4, -5/2, 0, 1, and -2. For instance, 3/4 qualifies as a rational number because it consists of integers as its numerator and denominator, with the denominator being non-zero.
Irrational Number:
An Irrational number is a number that cannot be represented as a simple fraction of two integers. Its decimal representation is both non-terminating and non-repeating. Notable examples include ( √2 ), ( π ) (π), and ( \π ) (π). For instance, ( √2 ) is irrational because its decimal expansion (approximately 1.41421356…) continues indefinitely without exhibiting any repetitive pattern.
To find the square root of 149, you can use various methods:
Prime Factorization Method: Decompose 149 into its prime factors and pair them. Then, determine the square root by taking one factor from each pair.
Estimation Method: Approximate the square root of 149 by identifying perfect squares near it and interpolating between them to get a close approximation.
Calculator: Use a calculator with a square root function to directly find the square root of 149.
Newton’s Method: Employ iterative approximation methods like Newton’s method to converge towards the square root of 149 through successive calculations based on initial guesses.
Choose the method that suits your preference and computational capabilities to find the square root of 149.
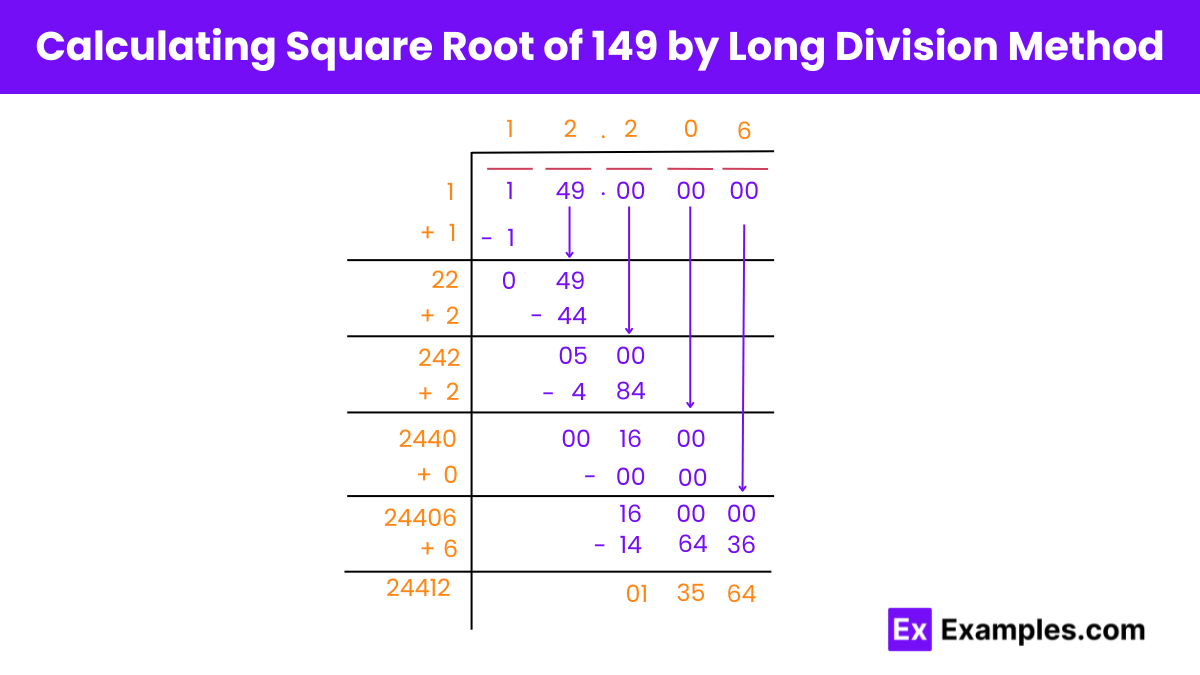
Calculating the Square Root of 149 Using Long Division Method
Digit Pairing: Begin by grouping the digits of 149 into pairs from the right: 49 and 1.
Finding Initial Quotient: Determine a number (N) whose square is ≤ 1. Since 1 × 1 = 1, N is 1. This gives us the initial quotient.
New Divisor: Double the initial divisor (N) to obtain the new divisor (2N = 2).
Dragging Down the Next Pair: Bring down the next pair of numbers (049) to form the new dividend.
Determining the Next Digit: Find a number (q) such that 2q × q ≤ 49. The value of q is 2.
Decimal Placement: Place a decimal point in both the dividend (at the end of 149) and the quotient (at the end of 12). Additionally, append three pairs of zeros to the dividend after the decimal.
Repeat Steps: Continue the process for the remaining three pairs of zeros.
Final Result: The square root of 149 is approximately 12.206 when calculated using the long division method.
No, 149 is not a perfect square.
No, 149 is not a perfect square because it cannot be expressed as the square of an integer. Therefore, the square root of 149 is an irrational number, approximately equal to 12.207.
The square root of 149 is important in mathematics as it represents a fundamental concept in algebra and number theory. It illustrates the relationship between a number and its square root and is utilized in various mathematical calculations and problem-solving scenarios.
No, the square root of 149 cannot be simplified further because it is an irrational number, meaning it cannot be expressed as a simple fraction or in radical form with integers.
The square root of 149 can be used in practical applications such as calculating distances, areas, or volumes in geometry, engineering, physics, and other scientific fields where measurements and calculations involving squares and square roots are required.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the square of 149?
22,201
22,401
22,601
22,801
Which of the following is the square root of 22,201?
147
148
149
150
Find the square root of 149 up to three decimal places
12.205
12.206
12.208
12.209
Which number, when squared, gives the nearest result to 22,000?
149
150
151
152
If x² = 22,201, what is the value of x?
147
148
149
150
Which number is closest to the square root of 149?
11.5
11.8
12.0
12.2
What is the difference between the squares of 150 and 149?
299
300
301
302
If the square root of x is 12.206, what is x?
148
149
150
151
Which of the following is the nearest square to 22,000?
148²
149²
150²
151²
Calculate the sum of the squares of 148 and 149.
43,201
43,300
43,401
43,500
Before you leave, take our quick quiz to enhance your learning!

