What is the square of 2025?
4050
1025
2025
4100625
of 10
Square & Square Root of 2025 – Examples, Methods, Calculation
Square & Square Root of 2025 – Examples, Methods, Calculation
In the realm of mathematics, specifically within algebraic studies, the concepts of squares and square roots are of paramount importance. Squaring a number, such as taking 2025 and multiplying it by itself to obtain 4100625, is a fundamental operation. This process is essential for exploring the properties of both rational numbers (those that can be expressed as a fraction of two integers) and irrational numbers (which cannot be neatly expressed as a fraction). Understanding these basic concepts enriches one’s grasp of mathematical relationships and patterns. Through the study of squares and square roots, one gains deeper insights into the structure and behavior of numbers, which is crucial for more advanced mathematical investigations.
Square of 2025
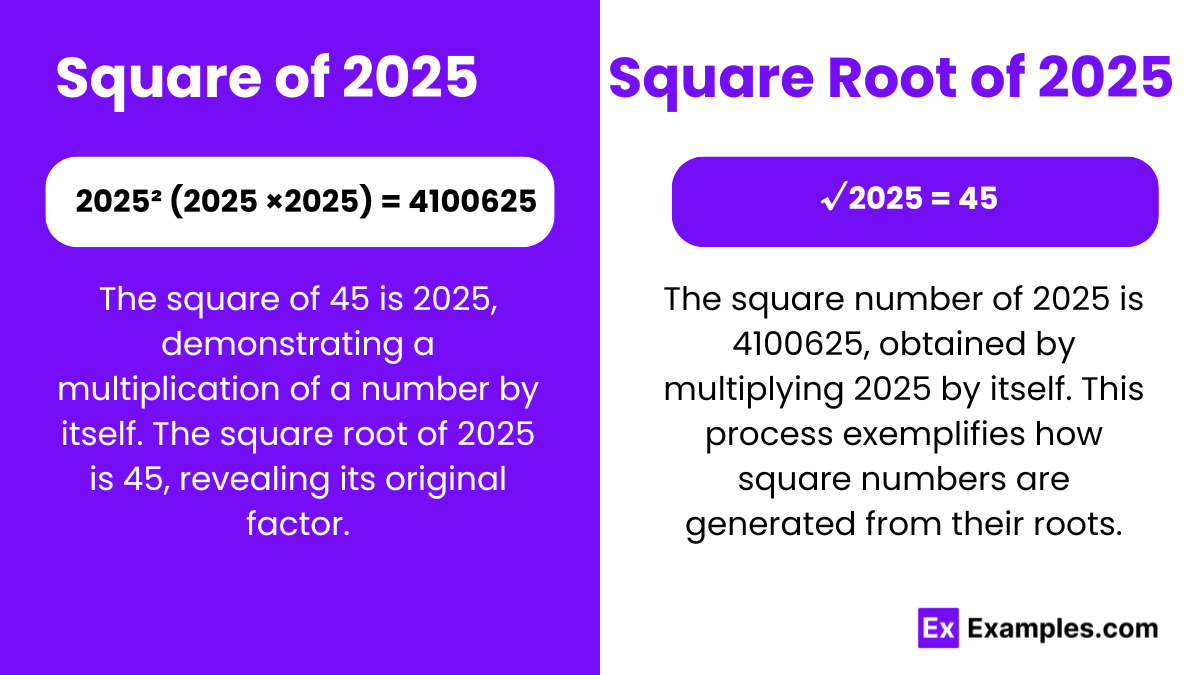
2025² (2025 × 2025) = 4100625
In algebraic mathematics, understanding square numbers is crucial. The square of 2025 is calculated by multiplying 2025 by itself, resulting in 4100625. This operation is fundamental for exploring the properties of both rational and irrational numbers, enhancing comprehension of mathematical relationships and patterns.
Square Root of 2025
√2025 = 45
In algebraic mathematics, the square root of 2025 is essential. Calculated as 45, it is the number which, when multiplied by itself, gives 2025. This operation is fundamental for understanding mathematical relationships and patterns involving both rational and irrational numbers.
Is the Square Root of 2025 Rational or Irrational?
The square root of 2025 is a rational number
The square root of 2025 is rational. This is because 2025 is a perfect square, and its square root is an integer: 45. Rational numbers are those that can be expressed as a fraction of two integers, and since 45 can be expressed as 45/1, it is a rational number.
Rational Number:
Definition: A rational number can be represented as a fraction of two integers, denoted as a/b, where b isn’t zero. Examples include positive, negative, or zero values, such as 3/4, -5/2, 0, 1, -2, etc.
Example: For instance, 3/4 is rational because both 3 and 4 are integers, and the denominator isn’t zero.
Irrational Number:
Definition: An irrational number, like √2 or π, cannot be expressed as a fraction of two integers. Its decimal expansion neither ends nor repeats, defying representation in the form a/b.
Example: √2 has a non-repeating, non-terminating decimal expansion (√2 ≈ 1.41421356…), making it irrational.
Method to Find Value of Root 2025
To find the value of the square root of 2025, you can use various methods, including:
Prime Factorization: Break down 2025 into its prime factors, which are 3, 3, 3, 3, 5, 5. Pair the prime factors and take one from each pair to get 3 × 5 = 15, making the square root of 2025 as 3 × 3 × 5 = 45.
Long Division: Using long division, find the square root by repeatedly dividing 2025 by increasing numbers until you reach a quotient close to the original number.
Estimation: Since 2025 is close to the square of 45 (which is 2025), you can estimate that the square root of 2025 is 45.
These methods can help you find the value of the square root of 2025 efficiently.
Square Root of 2025 by Long Division Method
Step 1: Forming Pairs
Identify pairs in the number: 20 and 25.
Step 2: Finding Initial Divisor
Find a number Y (4) such that its square is less than or equal to 20. Divide 20 by 4 to get the quotient as 4.
Step 3: Setting Up New Dividend
Bring down the next pair (25) to the right of the remainder (4). The new dividend becomes 425.
Step 4: Finding Next Digit of the Quotient
Add the last digit of the quotient (4) to the divisor (4), giving 4 + 4 = 8. Find a digit Z (5) such that 8Z × Z is less than or equal to 425. Together, 8 and Z (5) form a new divisor (85) for the new dividend (425).
Step 5: Division and Check for Remainder
Divide 425 by 85, resulting in a quotient of 5. Calculate the remainder as the difference between the dividend and the product of divisor and quotient (425 – 85 × 5 = 0).
Step 6: Conclusion
Stop the process since the remainder is now 0 and there are no more digits to bring down. Therefore, the square root of 2025, determined by the long division method, is 45.
2025 is Perfect Square root or Not?
No, 2025 is a perfect square number
Yes, 2025 is a perfect square because its square root is an integer (45). Therefore, 2025 can be expressed as the product of an integer multiplied by itself, making it a perfect square.
FAQS
How can understanding squares and square roots enrich mathematical comprehension?
Understanding squares and square roots deepens mathematical comprehension by revealing numerical relationships and patterns.
Can you explain the significance of the square of 2025 in mathematical contexts?
The square of 2025 holds significance in algebraic studies and serves as a fundamental example of a perfect square.
Are there any practical applications of knowing the square and square root of 2025?
Knowledge of the square and square root of 2025 can be applied in various mathematical and real-world scenarios, such as geometry and engineering calculations.
Where can I find more information about squares, square roots, and their relevance to mathematics?
You can find more information about squares, square roots, and their applications in mathematics textbooks, online resources, and educational websites.
Share :
Practice Test
If x is the square root of 2025, what is x²?
2025
4500
45
4578
of 10
Which number squared equals 2025?
30
35
40
45
of 10
What is the square of the number whose square root is 45?
2025
2050
2045
2100
of 10
Find the square of 2025.
4,050,625
4,050,000
4,500,000
4,500,625
of 10
What is 2025 divided by its square root?
45
50
100
150
of 10
If a number’s square is 2025, what is its square root?
50
55
45
40
of 10
What is the product of the square root of 2025 and 2?
70
80
90
100
of 10
The square of which number is closest to 2025?
44
45
46
47
of 10
What is the value of 2025 when reduced by its square root?
1975
1980
1985
1990
of 10