What is the square of 89?
7921
7919
7930
7941

Within algebraic studies, the significance of squares and square roots is foundational. Squaring a number, such as 2028, involves multiplying it by itself, yielding 4112784. This operation is pivotal in exploring properties of rational (expressible as a fraction) and irrational numbers. Understanding these concepts enriches comprehension of mathematical relationships and patterns. In algebra, squares and square roots are indispensable, serving as keystones in myriad calculations and analyses. They unlock deeper insights into numerical systems, bridging the realms of rationality and irrationality. Mastery of these fundamentals empowers mathematicians to navigate complexities, from basic arithmetic to advanced equations, fostering a holistic understanding of mathematical principles. Thus, the study of squares and square roots transcends mere computation, evolving into a profound exploration of mathematical structure and logic.
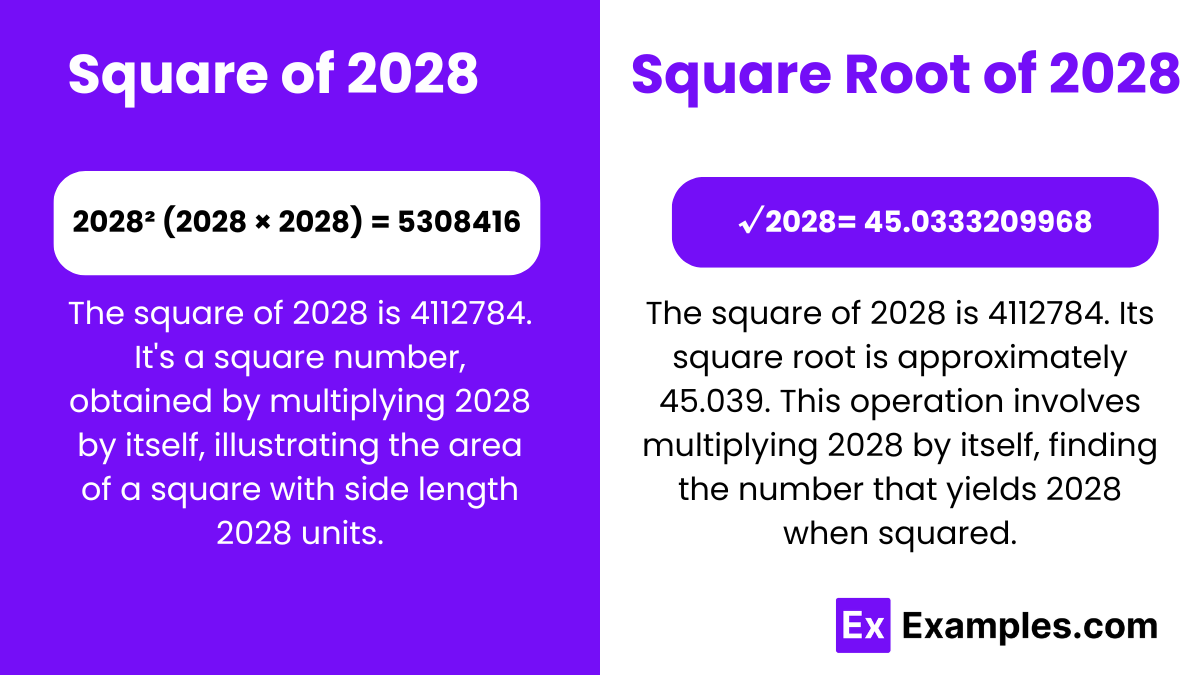
2028² (2028 × 2028) = 4112784
A square number results from multiplying an integer by itself. The square of 2028 is 4112784. In mathematics, square numbers exhibit distinct properties, crucial for understanding algebraic relationships and patterns. Exploring the square of 2028 unveils fundamental principles, enriching comprehension of mathematical structures and operations.
√2028 = 45.0333209968
Or
√2028 = 45.033 Upto 3 decimals
The square root, a fundamental concept in mathematics, reveals the number that, when multiplied by itself, yields the original number. The square root of 2028 is approximately 45.05. Understanding square roots elucidates the properties and relationships underlying numbers, offering insights into the square of 2028 and its mathematical significance.
Square Root of 2028: 45.0333209968
Exponential Form: 2028^½ or 2028^0.5
Radical Form: √2028
The square root of 2028 is an irrational number
The square root of 2028 is irrational. It cannot be expressed as a simple fraction of two integers. This characteristic distinguishes it from rational numbers, which can be represented in such a form.
The square root of 2028 is irrational. It cannot be expressed as a simple fraction. Its approximate value, about 45.05, is a non-repeating, non-terminating decimal. This classification highlights the intriguing complexity within mathematical systems, where some roots defy rational representation, adding depth to numerical exploration.
Rational number : A rational number is one expressible as a fraction of two integers, with a non-zero denominator. It can be written as a/b, where a and b are integers, and b ≠ 0.
Examples include 3/4, -5/2, 0, 1, and -2.
For instance, 3/4 can be represented as a fraction with 3 as the numerator and 4 as the denominator, meeting the criteria of being rational.
Irrational number : An irrational number, conversely, cannot be expressed as a ratio of two integers. Its decimal representation neither terminates nor repeats. Examples include √2, π, and φ.
For instance, √2 has an infinite decimal expansion (approximately 1.41421356…), and it lacks a repeating pattern. As it cannot be written as a fraction of two integers, √2 is classified as irrational.
Several methods can determine the square root of 2028:
Prime Factorization: Break down 2028 into its prime factors to simplify calculation.
Estimation: Use nearby perfect squares to approximate the root.
Newton’s Method: Iteratively refine guesses to converge on the precise value.
Calculator or Software: Utilize technology for accurate and rapid computation.
Long Division Method: Employ a step-by-step division process to extract the root manually.
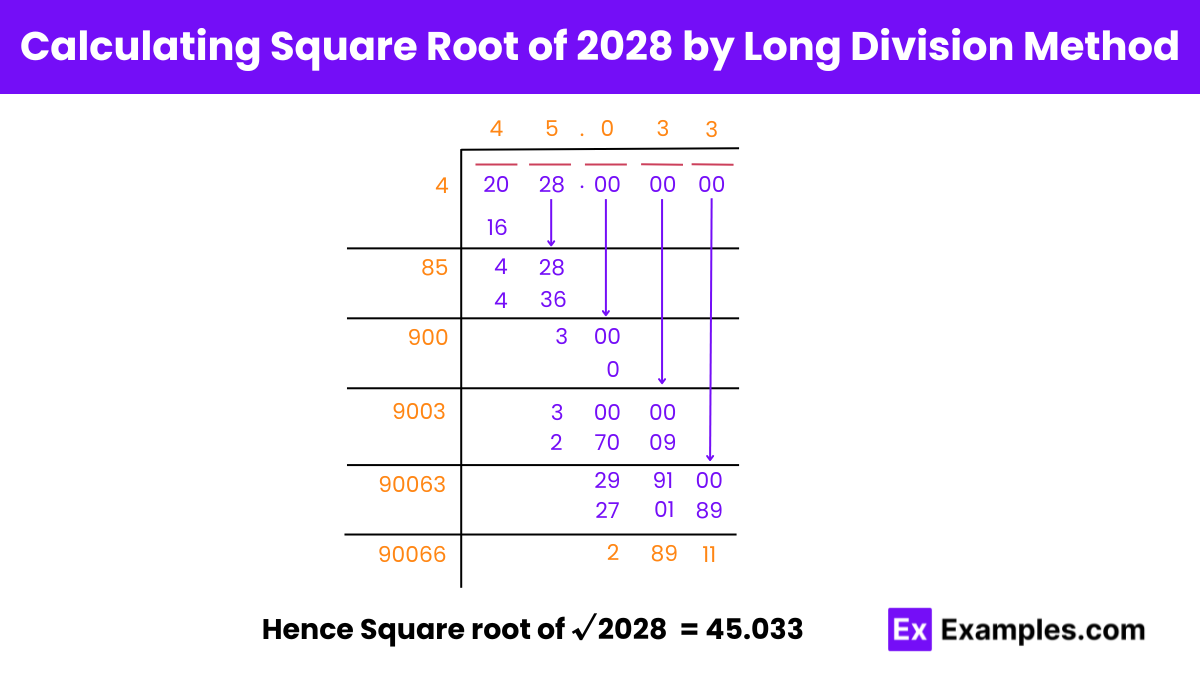
Step 1: Forming Pairs
Split the number 2028 into pairs: 20 and 28.
Step 2: Initial Division
Find a number Y (4) such that its square is less than or equal to 20. Divide 20 by 4, resulting in a quotient of 4.
Step 3: Continuing the Division
Bring down the next pair, 28, next to the remainder 4, forming the new dividend, 428.
Add the last digit of the quotient (4) to the divisor (4), yielding 8. Find a digit Z (5) such that 8Z × Z is less than or equal to 428. The new divisor becomes 85.
Divide 428 by 85, resulting in a quotient of 5 and a remainder of 3.
Step 4: Decimal Places
To find decimal places after the quotient 45, bring down 00 next to the remainder 3, forming the new dividend, 300.
Add the last digit of the quotient to the divisor (5 + 85 = 90). Find a digit Z (0) such that 90Z × Z is less than or equal to 300. The new divisor is 900.
Divide 300 by 900, resulting in a quotient of 0 and a remainder of 300.
Step 5: Conclusion
Repeat the steps to find more decimal places if needed. Thus, the square root of 2028 by the long division method is approximately 45.0.
No, 2028 is not a perfect square number
2028 is not a perfect square because it cannot be expressed as the square of an integer. Its square root is approximately 45.05, indicating that it is an irrational number. Perfect squares have integer square roots, which is not the case for 2028.
2028 is not a perfect square because it cannot be expressed as the product of an integer multiplied by itself.
The square root of 2028, approximately 45.05, helps understand its mathematical properties and relationships.
You can use methods like prime factorization or long division for manual calculation.
No, because it’s an irrational number, and 2028 is not a perfect square.
Understanding square roots is essential in various fields like engineering, physics, and finance for calculations involving area, volume, and risk analysis.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the square of 89?
7921
7919
7930
7941
What is the approximate value of √89?
9.3
9.4
9.5
9.6
Solve for x if x² = 89.
8.9
9.0
9.4
9.5
Simplify the square root of 89 to its decimal form.
9.32
9.34
9.36
9.43
What is the value of 89²?
7921
7932
7943
7954
Estimate the square root of 89 to the nearest tenth.
9.3
9.4
9.5
9.6
Which number is not a perfect square but is closest to 89?
81
85
91
93
Calculate the value of √89 raised to the power of 2.
88
89
90
91
What is the approximate value of √89 to one decimal place?
9.3
9.4
9.5
9.6
Find the number whose square root is approximately 9.4.
85
86
89
90
Before you leave, take our quick quiz to enhance your learning!

