What is the square of 22?
484
485
486
487


In algebraic mathematics, the fundamental concepts of squares and square roots are paramount. Squaring a number, such as multiplying 22 by itself to get 484, is foundational. This operation is crucial for exploring the properties of rational numbers (expressible as a fraction of two integers) and irrational numbers (defying neat fractional expression). Understanding these basics enriches comprehension of mathematical relationships and patterns.
A square number results from multiplying a number by itself. For instance, the square of 22 equals 484. In algebraic mathematics, understanding square numbers, like 22 squared, is fundamental for exploring numerical properties and patterns within rational and irrational numbers.
Or
√22 = 4.69 Upto 3 decimals
The square root of a number is the value that, when multiplied by itself, equals the original number. The square root of 22 is approximately 4.69. In algebraic studies, comprehending square roots, like that of 22, is vital for understanding numerical relationships and solving equations involving squares.
Square Root of 22: 4.69041575982
Exponential Form: 22^½ or 89^0.5
Radical Form: √22
The square root of 22 is irrational. This means it cannot be expressed as a fraction of two integers. It’s a non-repeating, non-terminating decimal, indicating its irrational nature.
Rational Number:
A rational number is any number that can be expressed as the quotient or fraction of two integers, where the denominator is not zero. In other words, it can be written in the form a/b, where a and b are integers and b is not equal to zero. Rational numbers can either be positive, negative, or zero. Examples include 3/4, -5/2, 0, 1, -2, etc.
Example: Let’s consider the number 3/4. It can be represented as a fraction, where 3 is the numerator and 4 is the denominator. Since both 3 and 4 are integers and the denominator is not zero, 3/4 is a rational number.
Irrational Number:
An irrational number is a real number that cannot be expressed as a ratio of two integers. In other words, its decimal representation neither terminates nor repeats, and it cannot be written in the form a/b, where a and b are integers and b is not equal to zero. Irrational numbers can be found on the number line but cannot be expressed as fractions. Examples include the square root of 2 (√2), pi (π), and the golden ratio (φ).
Example: Consider the square root of 2 (√2). Its decimal expansion is approximately 1.41421356…, and it continues infinitely without repeating. Since it cannot be written as a fraction of two integers, √2 is an irrational number.
There are several methods to find the value of the square root of 22:
Estimation: Use estimation techniques to approximate the square root of 22 to a reasonable decimal place.
Prime Factorization: Factorize 22 into its prime factors (2 x 11) and use properties of square roots to simplify.
Newton’s Method: Iterate using Newton’s method to approximate the square root of 22.
Using a Calculator: Utilize a scientific calculator or an online calculator to directly compute the square root of 22.
Binomial Expansion: Use binomial expansion techniques to approximate the square root of 22.
Each method has its own advantages and applicability depending on the level of accuracy required and the tools available.
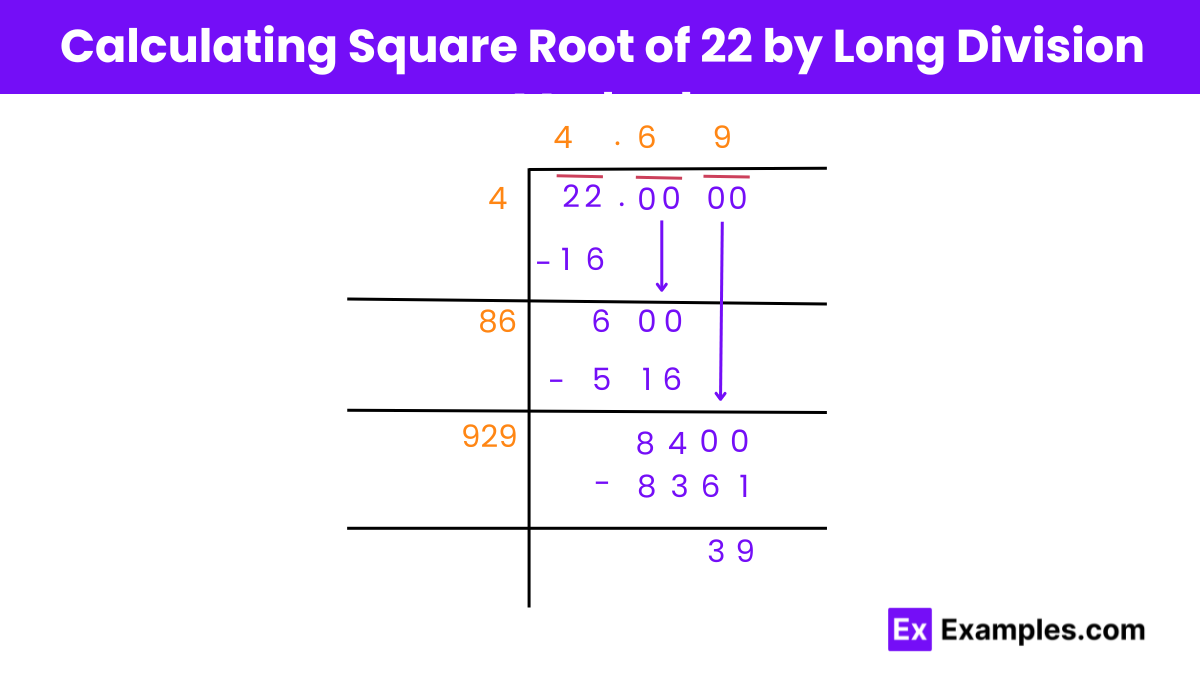
Finding the Square Root of 22 by Long Division
Step 1: Identify the Pair of Digits
Start with the pair of digits from the one’s place, which is 22 in this case.
Step 2: Find the Initial Divisor
Determine a divisor ‘n’ such that n × n is less than or equal to 22. Here, 4 is chosen since 4 × 4 = 16.
Step 3: Calculate the Quotient and Difference
Calculate the quotient (4) and the difference (22 – 16 = 6). Double the quotient to obtain the new divisor’s first digit (4 × 2 = 8).
Step 4: Introduce Decimal Point and Zeros
Add a decimal point to the dividend (22) and quotient (4). Place two pairs of zeros after the decimal point in the dividend and bring down the next pair of digits.
Step 5: Determine the Next Divisor
Identify a new divisor ‘n’ such that n × n is less than or equal to 600. The next quotient is 6, resulting in a new divisor of 86 (6 × 86 = 516).
Step 6: Continue the Process
Bring down the next pair of zeros and proceed with the long division.
Step 7: Refine the Divisor
Double the quotient (46) to obtain the new divisor’s first digit. Identify a divisor ‘n’ such that n × n is less than or equal to 8400.
Step 8: Conclude the Calculation
The long division process yields a quotient up to two decimal places. Thus, √22 ≈ 4.69. Further refinement may continue for more decimal accuracy.
No, 22 is not a perfect square number
22 is not a perfect square because it cannot be expressed as the square of an integer. In other words, there is no integer that, when multiplied by itself, equals 22. Therefore, the square root of 22 is an irrational number.
No, the square root of 22 cannot be expressed as a fraction because it is an irrational number.
The square root of 22 is greater than 4 but less than 5, making it approximately 4.69.
The square root of 22 to three decimal places is approximately 4.690.
The square root of 22 has infinitely many decimal places since it is an irrational number.
The square root of 22 (√22) is the number that, when multiplied by itself, equals 22. In other words, (√22)² = 22.
No, the square root of 22 is not a recurring decimal since it does not repeat infinitely.
Yes, the square root of 22 is a real number because it lies on the real number line.
The square root of 22 is between the square roots of 20 and 24. Specifically, it is closer to the square root of 25 (which is 5) than to the square root of 20.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the square of 22?
484
485
486
487
Which of the following is the closest approximation to the square root of 22?
4.6
4.7
4.8
4.9
If x² = 22, what is x?
4.6
4.7
4.8
4.9
What is the approximate value of √22 to two decimal places?
4.64
4.65
4.66
4.67
What is 22 squared?
462
484
506
528
Simplify √22 to its decimal form.
4.64
4.66
4.68
4.69
What is the square root of 22 rounded to the nearest whole number?
4
5
6
7
Which number is closest to 22 but not a perfect square?
16
20
25
26
Find the value of 22 × 22.
462
484
506
508
What is the nearest integer to the square root of 22?
4
5
6
7
Before you leave, take our quick quiz to enhance your learning!

