Square & Square Root of 2304
Square & Square Root of 2304
In algebraic studies, understanding squares and square roots is pivotal. Squaring, exemplified by 2304 multiplied by itself to yield 5308416, is foundational. This operation explores rational and irrational numbers’ properties. Rational numbers are fractions of integers, while irrationals defy neat fractions. Mastering these concepts enriches mathematical comprehension, revealing relationships and patterns.
Square of 2304
The square number of 2304 is 5,308,416, obtained by multiplying 2304 by itself. Squaring is fundamental in algebra, revealing properties of numbers and facilitating comprehension of mathematical relationships and patterns.
Square Root of 2304
The square root of 2304 is 48, found by determining the number which, when multiplied by itself, equals 2304. Understanding square roots enriches mathematical comprehension.
Square Root of 2304: 48
Exponential Form: 2304^½ or 2304^0.5
Radical Form: √2304
Is the Square Root of 2304 Rational or Irrational?
The square root of 2304 is rational because it equals 48, which can be expressed as a fraction of two integers.
Certainly!
Rational Numbers: Rational numbers are those that can be expressed as the quotient of two integers, where the denominator is not zero. They can be written in the form 𝑎𝑏ba, where 𝑎a and 𝑏b are integers and 𝑏≠0b=0. Rational numbers can be represented as fractions with finite or repeating decimals. Examples include fractions like 1/2, -3, and 5/5.
Irrational Numbers: Irrational numbers cannot be expressed as fractions of integers. They have decimal forms that continue infinitely without repeating. Irrational numbers cannot be represented as terminating or repeating decimals. Examples include the square roots of non-perfect squares like √2, √3, √5, as well as transcendental numbers like 𝜋 (pi).
In summary, rational numbers can be expressed as fractions with finite or repeating decimals, while irrational numbers cannot be expressed in this way, having non-repeating, non-terminating decimal expansions.
Methods to Find Value of Root 2304
There are several methods to find the square root of 2304:
Prime Factorization Method: Break down 2304 into prime factors, pair them up, and extract one factor from each pair to get the square root.
Estimation Method: Approximate the square root using known squares close to 2304 (e.g., 2304 is between 48² and 49²).
Long Division Method: Use long division to iteratively approximate the square root.
Using a Calculator: Input 2304 into a calculator and use the square root function.
Newton’s Method: Use iterative calculations to converge on the square root.
Each method has its advantages depending on the context and available resources.
Square Root of 2304 by Long Division Method
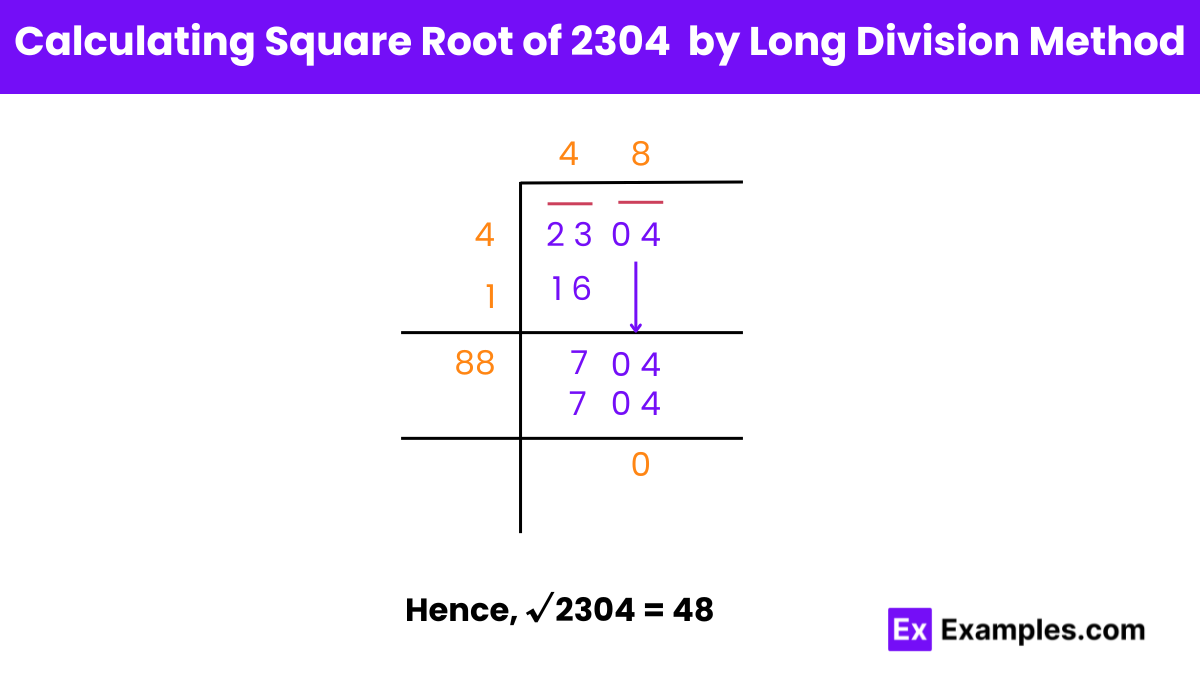
Sure, here’s a step-by-step explanation of finding the square root of 2304 using the long division method:
Forming pairs: Group the digits of 2304 into pairs: 23 and 04.
Finding the first digit (Y): Find a number Y such that Y squared is less than or equal to 23. Since 4 squared is 16 (which is less than 23), the first digit of the square root is 4. Divide 23 by 4, the quotient is also 4.
Bringing down the next pair: Bring down the next pair, 04, to the right of the remainder 7. The new dividend is now 704.
Finding the next digit (Z): Add the last digit of the quotient (4) to the divisor (4) to get 8. Find a digit Z such that 88 times Z is less than or equal to 704. Since 88 times 8 is 704, Z is 8. So, together 8 and 8 form a new divisor, 88.
Dividing: Divide 704 by 88, the quotient is 8, giving a remainder of 0.
Stopping the process: Since the remainder is now 0 and there are no more digits to bring down, we stop the process.
Therefore, the square root of 2304 by the long division method is 48.
Is 2304 Perfect Square root or Not
Yes, the number 1369 is a perfect square
Yes, 2304 is a perfect square. Its square root is 48 because 48 × 48 equals 2304. In mathematics, a perfect square is a number that can be expressed as the product of an integer multiplied by itself.
FAQ’S
What are the properties of the square and square root of 2304?
The square of 2304 is a large positive integer, while its square root is a rational number.
Why are the concepts of squares and square roots important?
Squares and square roots are fundamental in mathematics, aiding in understanding number properties, patterns, and solving equations.
Can 2304 be written as a product of prime factors?
Yes, the prime factorization of 2304 is 2⁸ × 3².
How do the concepts of squares and square roots relate to real-life applications?
They are used in various fields such as engineering, physics, and finance for calculations involving areas, distances, volumes, and more.
Share :
