What is the square of 38?
1368
1372
1444
1448
of 10
Square & Square Root of 38 – Examples, Methods, Calculation
Square & Square Root of 38 – Examples, Methods, Calculation
In the domain of mathematics, particularly within algebraic studies, the foundational principles of squares and square roots are pivotal. Squaring, demonstrated by multiplying a number like 38 by itself to yield 1444, is fundamental. It’s a cornerstone in exploring rational numbers (expressible as fractions of two integers) and irrational numbers (resisting neat fraction expression). Understanding these basics enriches comprehension of mathematical patterns and relationships, offering insights into the intricate fabric of mathematical theory.
Square of 38
38² (38 × 38) = 1444
The square of 38 is 1,444. A square number results from multiplying a number by itself. In this case, 38 multiplied by 38 equals 1,444. Square numbers are fundamental in mathematics, serving as the basis for exploring various concepts such as area, multiplication, and geometric properties.
Square Root of 38
√38 = 6.16441400297
Or
√38 = 6.164 Upto 3 decimals
The square root of 38 is approximately 6.164. The square root of a number is a value that, when multiplied by itself, equals the original number. Therefore, the square root of 38 represents the side length of a square with an area of 38 square units.
Square Root of 38: 6.16441400297
Exponential Form: 38^½ or 38^0.5
Radical Form: √38
Is the Square Root of 38 Rational or Irrational?
The square root of 38 is an irrational number
The square root of 38 is irrational. It cannot be expressed as a fraction of two integers. Its decimal representation is non-repeating and non-terminating, characteristic of irrational numbers.
Rational Number:
A rational number can be expressed as a fraction of two integers, denoted as a/b, where the denominator isn’t zero. Examples encompass positive, negative, or zero values, like 3/4, -5/2, 0, 1, -2, etc.
Example: For instance, consider 3/4; since both 3 and 4 are integers, and the denominator isn’t zero, 3/4 is rational.
Irrational Number:
An irrational number, such as √2 or π, cannot be expressed as a fraction of two integers. Its decimal expansion neither ends nor repeats, thus it defies representation in the form a/b.
Example: Take √2; it has a non-repeating, non-terminating decimal expansion (√2 ≈ 1.41421356…), rendering it irrational.
Method to Find Value of Root 38
To find the square root of 38, you can use various methods:
Estimation: Approximate the square root using nearby perfect squares (e.g., √36 = 6, √49 = 7) to get an initial guess.
Prime Factorization: Break down 38 into its prime factors (2 × 19) to simplify and find the square root.
Iteration: Use iterative algorithms like Newton’s method or the Babylonian method to refine an initial guess iteratively until convergence.
Calculator: Utilize a calculator or computer software to directly calculate the square root of 38.
Square Root of 38 by Long Division Method
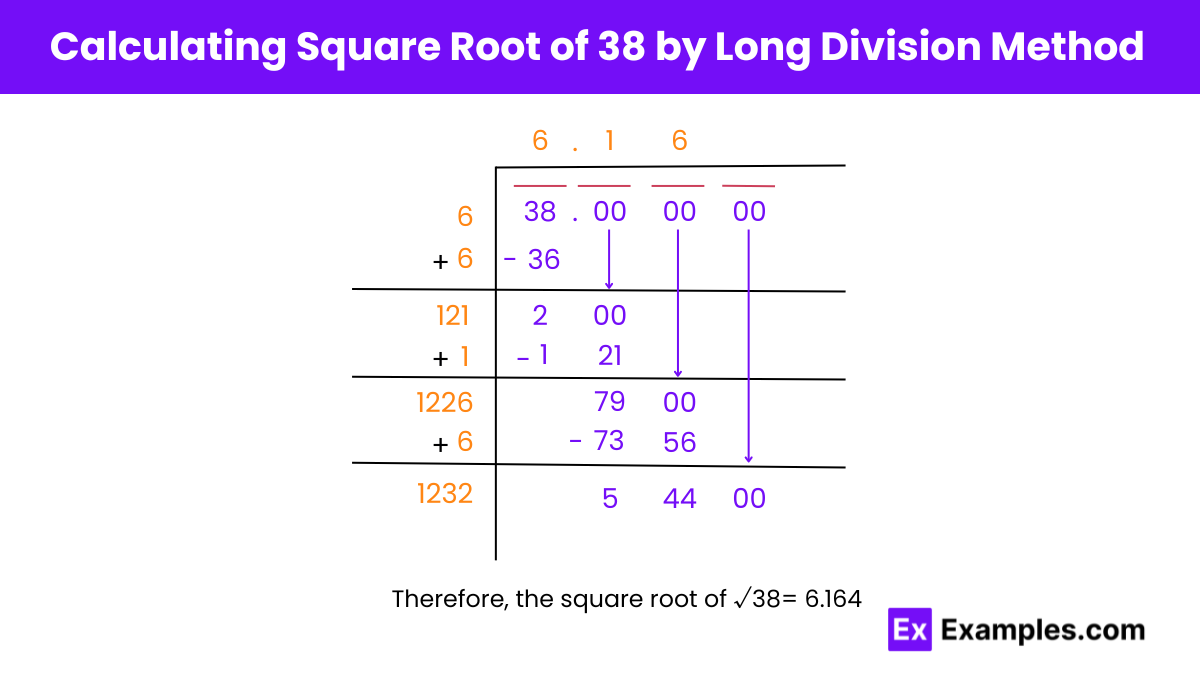
Long Division Method for Finding the Square Root of 38
Step 1: Pairing Digits
- Group the digits of 38 by placing a bar above them.
- Pair any decimal 0s from left to right.
Step 2: Initial Division
- Identify a number whose square is less than or equal to 38. In this case, 6 fits (6^2 = 36). Divide 38 by 6, resulting in a quotient of 6 and a remainder of 2.
Step 3: Updating Dividend
- Bring down a pair of 0s to the right of the remainder, making the new dividend 200.
Step 4: Iterative Division
- Double the previous quotient (6) to get 12. Leave a blank digit to its right.
- Guess the largest possible digit (X) to fill the blank, ensuring 12X × X is less than or equal to 200. In this case, X is 1, making the product 121. Subtract 121 from 200, leaving a remainder.
Step 5: Iterative Process
- Repeat the process to obtain additional decimal places as needed. Continue until the desired level of accuracy is reached.
38 is Perfect Square root or Not?
No, 38 is not a perfect square number
38 is not a perfect square because its square root is not an integer. The square root of 38 is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation goes on indefinitely without repeating.
FAQS
What is the square of 38 expressed in exponential form?
The square of 38 can be expressed as 38².
How does the square of 38 compare to other squares?
The square of 38 is larger than the squares of numbers less than 38 and smaller than the squares of numbers greater than 38.
What is the square root of 38 rounded to the nearest integer?
The square root of 38 rounded to the nearest integer is 6.
How many digits are there in the square root of 38?
The square root of 38 has an infinite number of digits after the decimal point.
What are some applications of the square root of 38 in real life?
The square root of 38 may be used in various mathematical calculations and engineering applications.
How can I verify if 38 is a perfect square?
You can check by finding its square root. If the square root is an integer, then 38 is a perfect square.
Share :
Practice Test
Which of the following is closest to the square root of 38?
6.1
6.2
6.3
6.4
of 10
If x² = 38, what is x?
6.1
6.2
6.3
6.4
of 10
Simplify √38 to its decimal form.
6.12
6.14
6.16
6.18
of 10
What is (38)²?
1369
1372
1444
1448
of 10
Find the approximate value of √38 to two decimal places.
6.10
6.12
6.14
6.16
of 10
Which number is not a square of an integer but closest to 38?
36
37
39
40
of 10
What is the value of 38 raised to the power of 0.5?
6.12
6.14
6.16
6.18
of 10
Calculate 38 × 38.
1368
1372
1440
1444
of 10
What is the approximate value of √38 between which two integers?
6 and 7
5 and 6
4 and 5
7 and 8
of 10