What is the square of 39?
1521
1530
1560
1570


In the vast realm of algebraic mathematics, the foundational concepts of squares and square roots stand as pillars of understanding. Squaring a number, as demonstrated by multiplying a value like 39 by itself to yield 1521, constitutes a fundamental operation. This process serves as a cornerstone in exploring the properties inherent in both rational numbers, expressible as fractions of two integers, and irrational numbers, which resist neat fractional expression. A grasp of these core concepts not only enriches comprehension of mathematical relationships but also unveils intricate patterns. Delving into the algebraic intricacies of squares and square roots unveils the profound interplay between numbers and operations, illuminating the inherent beauty and complexity of mathematical theory.
39²(39 × 39) = 1521
A square number, such as 39, results from multiplying a number by itself. The square of 39 is 1521. Understanding square numbers illuminates fundamental mathematical concepts, revealing the relationship between the original number and its square, essential for grasping algebraic principles and numerical patterns in mathematical analysis.
√39 = 6.2449979984
Or
√39 = 6.2449 Upto 3 decimals
The square root of 39, denoted as √39, is an irrational number, approximately equal to 6.2449979984. It represents the number that, when multiplied by itself, equals 39. Understanding square roots is essential in mathematics, unveiling the intricacies of numbers and their relationships, fundamental for algebraic investigations and problem-solving.
Square Root of 39 : 6.2449979984
Exponential Form : 39^½ or 39^0.5
Radical Form : √39
The square root of 39 is irrational.
The square root of 39 is an irrational number. This means it cannot be expressed as a fraction of two integers and its decimal representation goes on infinitely without repeating.
Certainly! Here’s a rewritten version:
Sure, here’s a revised version:
Rational Number:
A rational number is a fraction of two integers, expressed as a/b, where a and b are integers and b ≠ 0. Examples include 3/4, -5/2, 0, 1, and -2.
Example: 3/4 is rational because it’s a fraction with both numerator and denominator as integers, and the denominator isn’t zero.
Irrational Number:
An irrational number cannot be expressed as a ratio of two integers. Its decimal representation is non-terminating and non-repeating. Examples include √2, π, and φ.
Example: The square root of 2’s decimal expansion is approximately 1.41421356…, non-repeating and infinite, hence it’s irrational.
There are several methods to find the value of the square root of 39:
Prime Factorization Method: Express 39 as a product of its prime factors (3 × 13), then take the square root of each prime factor and multiply them together.
Estimation Method: Approximate the square root of 39 by considering it between the square roots of consecutive perfect squares (e.g., between √36 and √49).
Long Division Method: Use the long division method to find the square root of 39 iteratively, similar to how one would perform long division with numbers.
Calculator: Utilize a calculator or a mathematical software to directly calculate the square root of 39.
Each method offers its advantages depending on the level of precision required and the resources available.
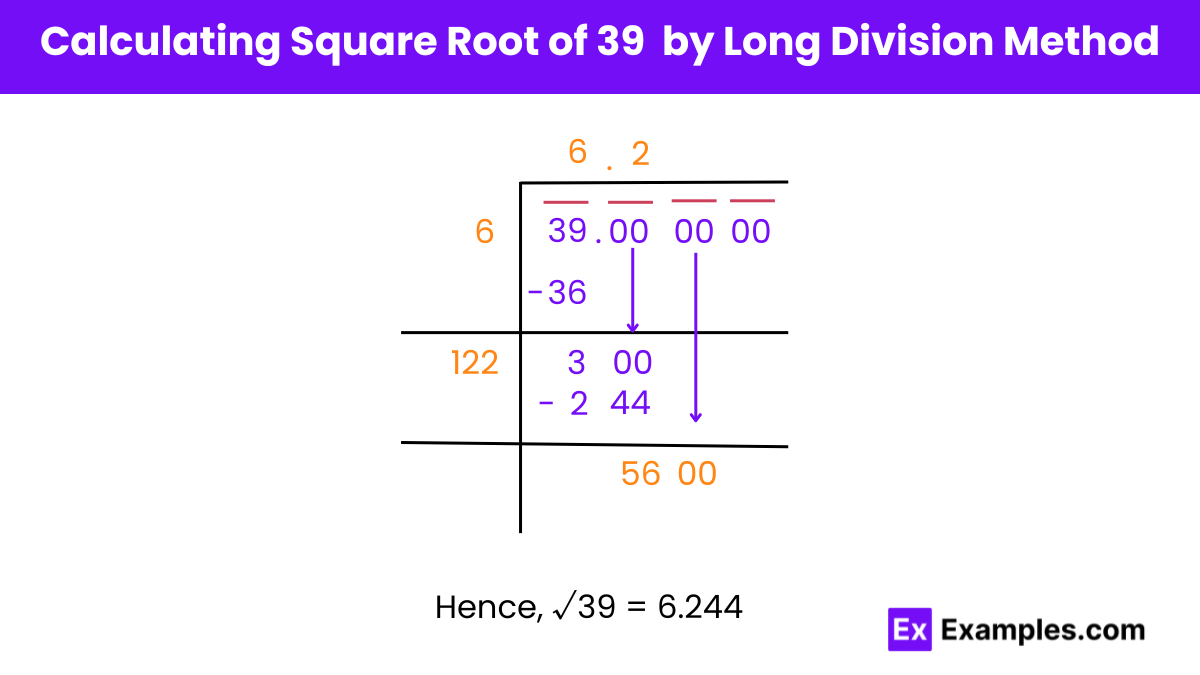
Certainly, here are the steps rewritten with subheadings:
Square Root of 39 by Long Division Method
Step 1: Grouping Digits
Starting from the right, pair up the digits 39 by placing a bar above 39. Pair the 0s in decimals in groups of two from left to right.
Step 2: Finding Initial Quotient
Find a number that, when multiplied by itself, gives a product less than or equal to 39. The number 6 fits here as 6^2 gives 36. Divide 39 by 6, with the quotient as 6, and the remainder as 3.
Step 3: Adding Zeros to the Dividend
Drag a pair of 0s down and place them next to 3 to make the dividend 300.
Step 4: Doubling the Divisor
Double the divisor 6, and place 12 as the divisor with a blank digit on its right. Find a number greater than or equal to the dividend, i.e., 300. 122 is the perfect number to divide 300.
Step 5: Multiplying and Finding Remainder
Multiply 122 by 2. 122 × 2 = 244, which is less than 300. Write the remainder, i.e., 56.
Step 6: Repeating the Process
Repeat this process until you achieve the desired quotient.
No, 39 is not a perfect square.
No, 39 is not a perfect square root. A perfect square root is a number that can be expressed as the product of an integer multiplied by itself. For example, 4 is a perfect square root because it is equal to 2 × 2, and 9 is a perfect square root because it is equal to 3 × 3. However, there is no integer that can be multiplied by itself to yield 39. Therefore, 39 is not a perfect square root.
The square root of 39 is greater than 6 and less than 7. It is also a non-terminating, non-repeating decimal.
The square root of 39 may be used in various real-life situations such as calculating distances, areas, or volumes in geometry, engineering, physics, or finance.
You can verify this approximation by squaring 6.2449979984 and checking if the result is close to 39.
No, the square root of 39 is an irrational number, so it cannot be simplified into a rational number.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the square of 39?
1521
1530
1560
1570
Which of the following is the closest approximation to the square root of 39?
6.2
6.3
6.4
6.5
What is √39 rounded to the nearest whole number?
5
6
7
8
If x² = 39, what is x approximately?
6.2
6.3
6.4
6.5
Calculate √39 to two decimal places.
6.22
6.24
6.26
6.28
What is (√39)²?
37
38
39
40
Find the result of squaring √39.
36
39
40
43
What is the cube of √39?
230
240
250
260
Determine the value of 39 raised to the power of 0.5.
6.2
6.3
6.4
6.5
What is the exact result of squaring 39?
1530
1521
1540
1560
Before you leave, take our quick quiz to enhance your learning!

