Square & Square Root of 500 – Examples, Methods, Calculation

In algebraic studies within mathematics, the concepts of squares and square roots are crucial. Squaring a number, such as 500, involves multiplying it by itself to get 250,000. This fundamental operation is essential for exploring the properties of rational numbers (expressible as a fraction of two integers) and irrational numbers (which cannot be expressed as a simple fraction). Understanding these basic concepts enhances one’s grasp of mathematical relationships and patterns. The study of squares and square roots not only lays the groundwork for more complex mathematical theories but also aids in recognizing the intrinsic connections between numbers, fostering a deeper appreciation of the logical structure within mathematics.

Square of 500

In mathematics, a square number is the result of multiplying a number by itself. The square of 500 is 250,000. Understanding square numbers, like 250,000, helps in exploring both rational and irrational numbers, deepening comprehension of mathematical relationships and patterns within algebraic studies.

Square Root of 500

The square root of 500 is approximately 22.36. This value is found by determining the number which, when multiplied by itself, equals 500. Understanding square roots, like 22.36, is essential in algebraic studies for exploring properties of rational and irrational numbers in mathematics.

Is the Square Root of 500 Rational or Irrational?

The square root of 500 is an irrational number, approximately 22.36, as it cannot be expressed as a simple fraction of two integers.

Rational Numbers:

A rational number is any number that can be expressed as the fraction of two integers, where the numerator and the denominator are both integers, and the denominator is not zero. The format for rational numbers is typically written as 𝑎/𝑏a/b. These numbers can be positive, negative, or zero, such as 3/43/4, −5/2−5/2, 00, 11, and −2−2.

Example: Consider the fraction 3/43/4; since 33 and 44 are both integers and 44 is not zero, 3/43/4 qualifies as a rational number.

Irrational Numbers:

An irrational number cannot be expressed as a fraction of two integers. These numbers have decimal expansions that are infinite and non-repeating, making them impossible to represent as 𝑎/𝑏a/b. Common examples of irrational numbers include 22​ and 𝜋π.

Example: Look at 22​. It has a decimal expansion that does not terminate or repeat, approximately 1.41421356…1.41421356…, which classifies it as an irrational number.

Method to Find Value of Root 500

To find the value of the 500th root of a number, ( x ), you can use the mathematical formula:

[ x¹/⁵⁰⁰ ]

This formula represents taking the 500th root of ( x ). Here’s a step-by-step method to calculate this using basic mathematical tools or a scientific calculator:

Identify the Number: First, determine the number ( x ) of which you want to find the 500th root.

Use a Calculator: Most scientific calculators have a function for taking ( n )th roots or for raising a number to the power of a fraction. To calculate ( x¹/⁵⁰⁰ ), you can use the power function on your calculator:

Enter the number ( x ).

Press the exponentiation key (often labeled as ( yˣ ),pow or a similar notation).

Enter the fraction ( 1/500 ).

Manual Calculation (if needed): If you don’t have access to a scientific calculator that can compute fractional powers directly, you can transform the calculation into a logarithmic form to make it simpler using a basic calculator:

Compute the logarithm of ( x ), usually base 10 or natural logarithm (ln).

Divide the logarithm by 500.

Take the anti-logarithm (if you used base 10, take the power of 10; if natural, use ( e )) of the result from the previous step.

Computer Software or Online Tools: You can also use computer software like Python, MATLAB, or online calculators to perform this calculation simply by entering the formula for ( x¹/⁵⁰⁰ ).

If you provide a specific number, I can calculate its 500th root for you right here!

Square Root of 500 by Long Division Method

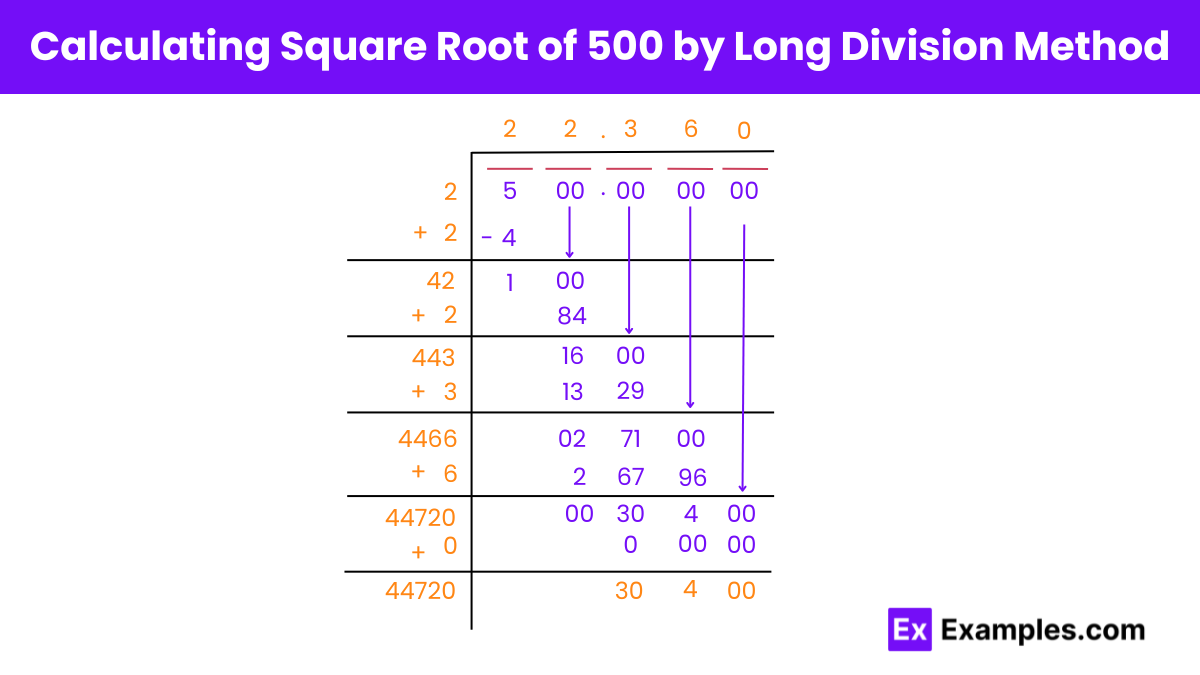
Here’s how to calculate the square root of 500 using the long division method, organized into clear subheadings for each step:

1. Pair the Digits

Start by pairing the digits from the right. For the number 500, create two pairs: 00 and 5. Since there are fewer than two digits in the leftmost pair, we just use 5.

2. Find the Initial Divisor

Identify a number ( y ) whose square is less than or equal to 5. In this case, ( y = 2 ) because ( 2 \times 2 = 4 ), which is less than 5.

3. Subtract and Bring Down Next Pair

After determining ( y ), subtract ( y² ) from the first pair. The remainder is 1. Now, double the divisor ( y ) (which is 2) to get the next divisor, ( 2y = 4 ). Bring down the next pair (00), making the new dividend 100.

4. Determine the Next Digit of the Root

Find a digit ( a ) such that ( (4a) \times a \leq 100 ). Here, ( a = 2 ) because ( (4 × 2) × 2 = 16 × 2 = 32 ), which is less than 100.

5. Add Decimals and Continue the Division

Place a decimal point in the quotient (22) and the dividend (100) right after the initial calculation, then add three pairs of zeros to the dividend due to the decimal expansion. Repeat the previous step with the new dividend and divisor to find subsequent digits of the square root.

6. Conclusion

Following these steps, you continue the division process to achieve more decimal accuracy. For our example, after repeating these steps sufficiently, we approximate the square root of 500 to be about 22.360.

500 is Perfect Square root or Not?

500 is not a perfect square. A perfect square is a number that can be expressed as the square of an integer. The square root of 500 is approximately 22.36, which is not an integer, confirming that 500 is not a perfect square.

FAQs