Square & Square Root of 529 – Methods , Calculations , Examples

Exploring the square and square root of numbers offers fundamental insights into algebraic principles. This guide delves into the number 529, illustrating how squaring it yields 279,841, while its square root simplifies to 23. These operations are not just mathematics exercises; they reveal underlying patterns and relationships within numbers. Understanding how to compute squares and square roots is essential for solving a variety of mathematical problems, from basic algebra to complex geometry. By examining 529 in this detailed manner, we can appreciate the precision and elegance of mathematical operations and their applications across different fields of study.

Square of 529

The square of 529 refers to the result of multiplying the number 529 by itself. In mathematical terms, this operation is represented as 529². When you calculate 529 squared, it equals 279,841. This arithmetic operation is fundamental in various mathematical areas, such as geometry, where it helps in calculating area, and in algebra for understanding the properties of numbers and equations. Squaring a number essentially multiplies it by its own value, expanding its magnitude exponentially and illustrating the growth rate when numbers are raised to the power of two.

Square Root of 529

The square root of 529 refers to the number that, when multiplied by itself, yields 529. Mathematically, this is expressed as √529​. For the number 529, the square root is 23, because 23×23=529. Understanding square roots is crucial in mathematics for solving quadratic equations, calculating geometric dimensions, and handling various operations that require reversing the squaring process. It’s a key concept in both academic studies and real-world applications where determining original quantities from squared results is necessary.

Is the Square Root of 529 Rational or Irrational?

Rational:

The square root of 529 is rational. A rational number is defined as a number that can be expressed as the fraction 𝑝/𝑞​, where 𝑝 and 𝑞 are integers, and 𝑞 is not zero. The square root of 529 is 23, which can be expressed as 23/1​. It fits the definition of a rational number because it results in an integer without any need for an infinite or non-repeating decimal.

Irrational:

The square root of 529 is not irrational. Irrational numbers are those that cannot be expressed as a fraction of two integers, where the denominator is not zero. They are characterized by non-repeating, non-terminating decimal expansions. However, since the square root of 529 is 23, a whole number, it does not fit the criteria for being irrational.

Methods to Find the Value of Root 529

1. Using a Calculator

The simplest and most accurate way to find the square root of 529 is by using a calculator. Most calculators have a square root function. Simply enter 529 and press the square root button to get the result.

2. Prime Factorization

Prime factorization involves breaking down a number into its prime factors. The prime factors of 529 are 23 x 23. Since the prime factors are a perfect square, the square root of 529 is 23.

3. Guess and Check Method

Start with an initial guess for the square root. Since 529 is between the squares of 20 (400) and 30 (900), start with 25. Squaring 25 gives 625, which is too high. Try a lower number, like 23. Squaring 23 results in 529, which is the perfect square root.

4. Using Approximation

For numbers that are not perfect squares, approximation methods such as the Babylonian method (or Newton-Raphson method) can be used. However, since 529 is a perfect square, approximation typically isn’t necessary. The steps for the Babylonian method involve making a guess and iteratively improving the guess by averaging the guess and the result of dividing the original number by the guess.

5. Using a Square Root Table

Before calculators became commonplace, square root tables were a handy reference for finding square roots. These tables list the squares of numbers and their corresponding roots. For 529, you would simply find the number in the square column and see that its square root is 23.

Square Root of 529 by Long Division Method

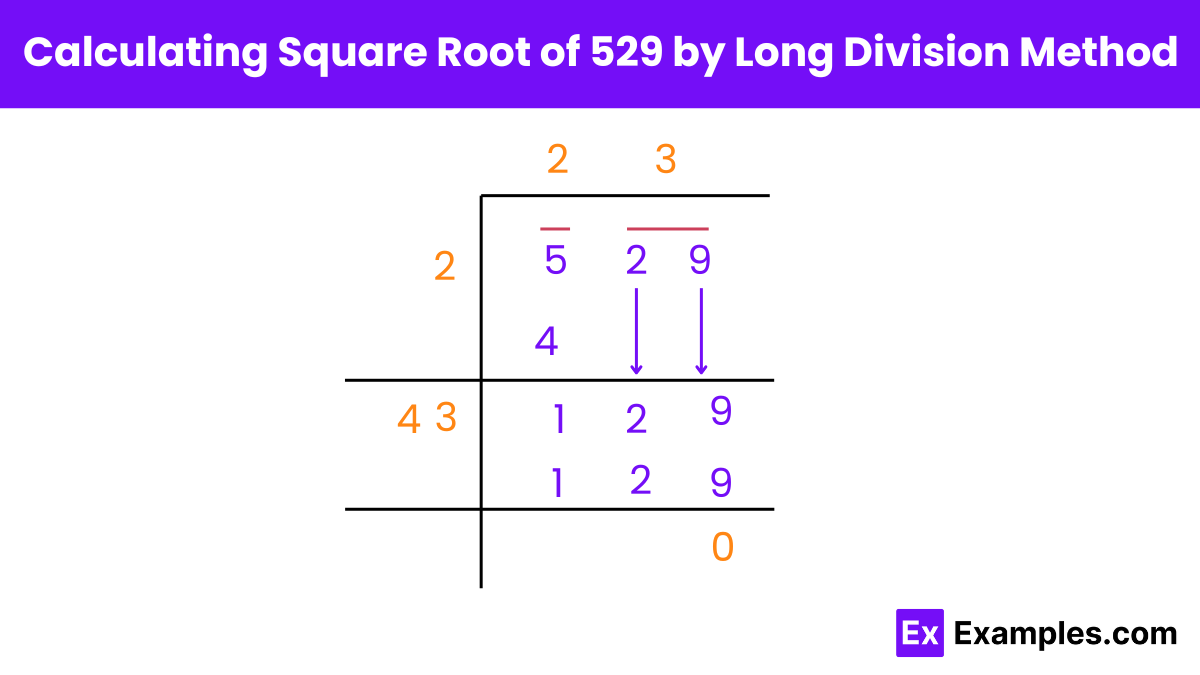
The long division method is a step-by-step manual process to find the square root of a number. This method is particularly useful for larger numbers or when a calculator is not available. Here, we will demonstrate how to find the square root of 529 using the long division method.

1. Set up the number:
   • Write 529, and pair the digits from right to left into groups of two (if there’s an odd number of digits, the leftmost group may be a single digit). For 529, we have two groups: 5 and 29.
2. Find the largest square less than or equal to the first group:
   • The first group is 5. The largest perfect square less than or equal to 5 is 4 (2^2).
   • Write 2 as the first digit of the result above the square root line.
3. Subtract the square of 2 from the first group and bring down the next group:
   • Subtract 4 from 5, you get 1.
   • Bring down the next group (29), making it 129.
4. Double the result found (which is now the divisor) and find a new digit:
   • Double 2 (the current quotient), which gives 4.
   • Place a 3 next to 4, making it 43, and find the largest number that when multiplied by 43 results in 129 or less. The number 3 fits, because 43 multiplied by 3 equals 129.
5. Perform the subtraction and find the remainder:
   • Subtract 129 from 129, resulting in 0.
6. Repeat the process if necessary:
   • Since there are no more digits to bring down and the remainder is 0, we conclude the process here.
7. Combine the digits above the line for the final result:
   • The digits above the line form the number 23.

529 is Perfect Square root or Not?

Yes, 529 is a perfect square. A perfect square is a number that can be expressed as the square of an integer. In the case of 529, it is the square of 23 (since 23×23=52923×23=529). This means that the square root of 529 is exactly 23, without any fractional or decimal component, confirming it as a perfect square.

FAQS

Is there a quick way to find the square root of 529 without a calculator?

A quick method without a calculator is to recognize that 529 is a number ending in 9 and its square root might end in 3 or 7. Testing these, 23×23=529 confirms that 23 is the square root

Can you use the prime factorization method to find the square root of 529?

Yes, by prime factorization, 529 breaks down into 23×2323×23, and thus the square root is 23.

What are the real-world applications of knowing the square root of 529?

Knowing the square root is useful in mathematical problems involving area calculations, engineering designs, and statistical formulas.

How does the guess and check method work for finding the square root of 529?

You make an educated guess (e.g., between 20 and 30), then refine the guess based on squaring the numbers until you reach 529.

How can errors in calculating the square root of 529 affect professional fields like engineering?

Errors in calculating the square root can lead to incorrect dimensions or tolerances in engineering projects, potentially resulting in structural weaknesses or failures.