Square & Square Root of 54 – Examples, Methods, Calculation

In the realm of mathematics, particularly within algebraic studies, squares and square roots play a pivotal role. Squaring a number, like 54, to obtain 2916, is a fundamental operation, pivotal for exploring the properties of rational and irrational numbers. Understanding these concepts enriches comprehension of mathematical relationships and patterns.

Square of 54

The square of 54, a square number, is 2916. Squaring 54 entails multiplying it by itself, showcasing a fundamental mathematical operation. Understanding the properties of square numbers like 54 aids in comprehending mathematical concepts and relationships, contributing to a deeper understanding of numerical systems and their applications.

Square Root of 54

The square root of 54, an irrational number, is approximately 7.3484692283495345. It represents the number that, when multiplied by itself, equals 54. Understanding square roots illuminates mathematical principles, offering insights into numerical relationships and facilitating problem-solving across various disciplines.

Is the Square Root of 54 Rational or Irrational?

The square root of 54 is irrational, as it cannot be expressed as a fraction of two integers. Approximated to about 7.35, it signifies a non-repeating, non-terminating decimal. This characteristic distinguishes it from rational numbers, showcasing the diverse nature of mathematical expressions.

Rational Number:
A rational number is expressible as a fraction of two integers, where the denominator isn’t zero, denoted as a/b. Examples encompass positive, negative, or zero values, like 3/4, -5/2, 0, 1, -2, etc.

Example: Take 3/4; as both 3 and 4 are integers, and the denominator isn’t zero, 3/4 is rational.

Irrational Number:
An irrational number, like √2 or π, can’t be expressed as a fraction of two integers. Its decimal expansion neither ends nor repeats, thus defying the a/b form.

Example: √2 has a non-repeating, non-terminating decimal expansion (√2 ≈ 1.41421356…), making it irrational.

Methods to Find Value of Root 54

To find the square root of 54, several methods can be utilized:

Prime Factorization: Express 54 as a product of prime numbers (2 × 3^3) and simplify to find the square root.

Long Division: Employ long division to iteratively approximate the square root of 54.

Estimation: Use estimation techniques to approximate the square root of 54 by comparing it to nearby perfect squares.

Newton’s Method: Apply Newton’s method, an iterative numerical approximation technique, to find the square root of 54.

Square Root of 54 by Long Division Method

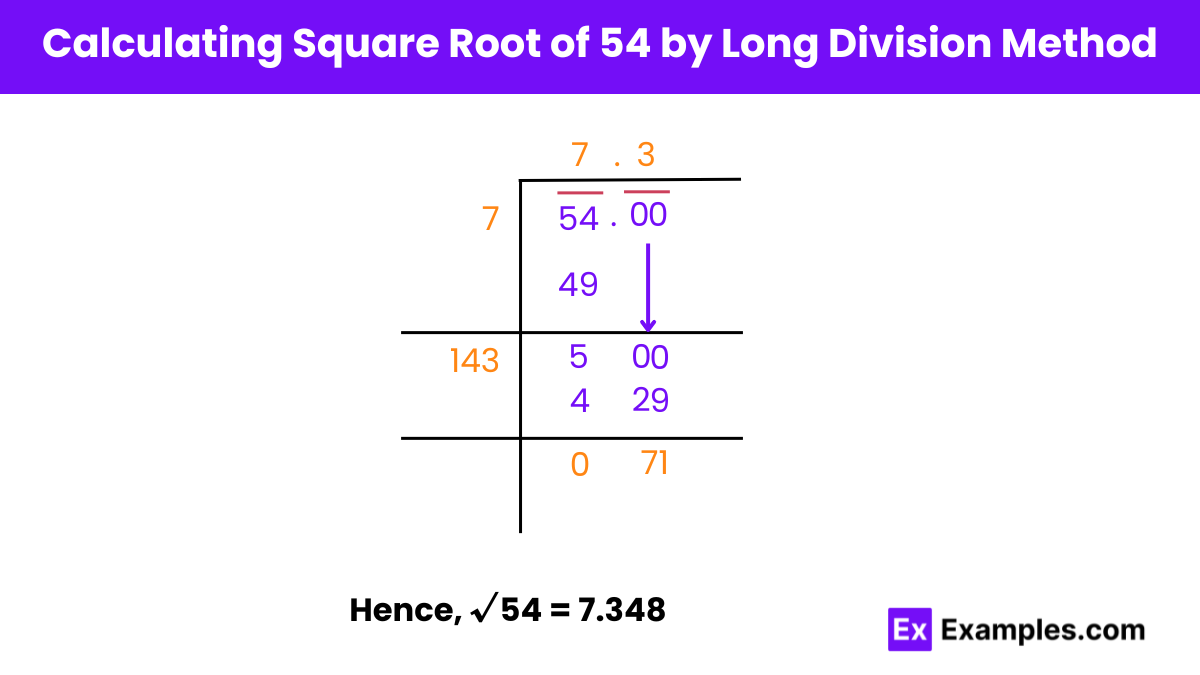
Finding Square Root of 54 by Long Division

Step 1: Pairing Digits
Create pairs of digits from the one’s place by placing a bar over them.

Step 2: Initial Division
Identify a number whose square is less than or equal to 54. Since 7 × 7 = 49, proceed with dividing 54 by 7.

Step 3: Decimal Point Placement
Place a decimal point in the quotient and add pairs of zeros to continue the division process. Multiply the quotient by 2 to determine the starting digit of the next divisor.

Step 4: Continuing Division
Select a digit for the new divisor, ensuring that its product with a number results in a value less than or equal to 500. Since the digit in the ten’s place is 3 and the product needs to be close to 500, choose 143 × 3 = 429 as the closest multiplication. Adjust the long division accordingly.

54 is Perfect Square root or Not

54 is not a perfect square. A perfect square is a number that can be expressed as the square of an integer. Since 54 cannot be expressed as the square of an integer, it is not a perfect square. Therefore, its square root is an irrational number.

FAQs

Is the square root of 54 a whole number?

No, the square root of 54 is not a whole number; it is approximately 7.348.

What is the significance of the square root of 54 in geometry?

It can be used to calculate the length of the sides of a square with an area of 54 square units.

Can the square root of 54 be expressed as a radical?

Yes, it can be expressed as √54, but it cannot be simplified further since it is an irrational number.

In what real-life scenarios would one encounter the square root of 54?

It may be used in construction projects to determine the length of diagonal lines in squares or rectangles with an area of 54 square units.

Is the process of finding the square root of 54 reversible?

No, while it’s possible to find the square root of 54, reversing the process to find the original number isn’t straightforward due to its irrational nature.