What is the square of 55?
3020
3025
3030
3035


In the field of mathematics, particularly in algebraic studies, the concepts of squares and square roots are crucial. Squaring a number involves multiplying it by itself, as seen when 55 is squared to produce 3025. This operation is essential for exploring the properties of rational numbers, which can be expressed as a fraction of two integers, and irrational numbers, which cannot be neatly represented as a fraction. Understanding these basic operations enhances one’s grasp of the intricate relationships and patterns within mathematics. Thus, squares and square roots form a fundamental part of algebraic concepts, bridging simpler arithmetic and more complex mathematical theories.
55² (55 × 55) = 3025
The square number of 55 is a square number resulting from multiplying 55 by itself, yielding 3025. This operation exemplifies basic algebraic concepts, highlighting the significance of square numbers in understanding mathematical patterns and relationships.
√55 = 7.4161984871
Or
√55 = 7.416 Upto 3 decimals
The square root of 55 is the number that, when multiplied by itself, equals 55. It’s approximately 7.416. This value is a critical component in algebra, demonstrating the concept of a square number and its role in deeper mathematical analysis and theory.
Square Root of 55: 7.4161984871
Exponential Form: 55^½ or 55^0.5
Radical Form: √55
The square root of 55 is an irrational number
The square root of 55 is irrational. This is because 55 is not a perfect square, meaning it cannot be expressed as the square of any integer. The decimal expansion of an irrational number is non-repeating and non-terminating, as is the case with the square root of 55.
Rational numbers: A rational number is defined as one that can be expressed as the fraction of two integers, examples include 3/4 or -5/2.
Irrational number: An irrational number is a number that cannot be written as a fraction of two integers. Its decimal expansion is non-terminating and non-repeating. For instance, the square root of 2 (√2) is approximately 1.41421356…, and is classified as irrational.
To find the value of the square root of 55, you can use several methods. Here’s a simplified explanation of a few common ones:
Identify perfect squares close to 55, such as 49 (7²) and 64 (8²).
Estimate that the square root of 55 is between 7 and 8.
Refine your estimate with more precision if needed.
This is a manual process similar to traditional long division.
Begin by pairing the digits of 55 from right to left (since 55 has only two digits, it remains as 55).
Find a number (7) whose square is less than or closest to 55.
Subtract the square of 7 from 55, drop down pairs of zeros (if needed), and continue the process to get more decimal points.
The simplest method is to use a calculator.
Just type in “square root of 55” or “√55” to get an immediate and accurate value.
Start with an initial guess (e.g., 7.5).
Use the formula: New estimate = 0.5 × (Old estimate + 55 / Old estimate) to iteratively approximate the square root.
Repeat the process until the change between successive estimates is acceptably small.
Each of these methods can help you determine the square root of 55, with varying degrees of effort and precision.
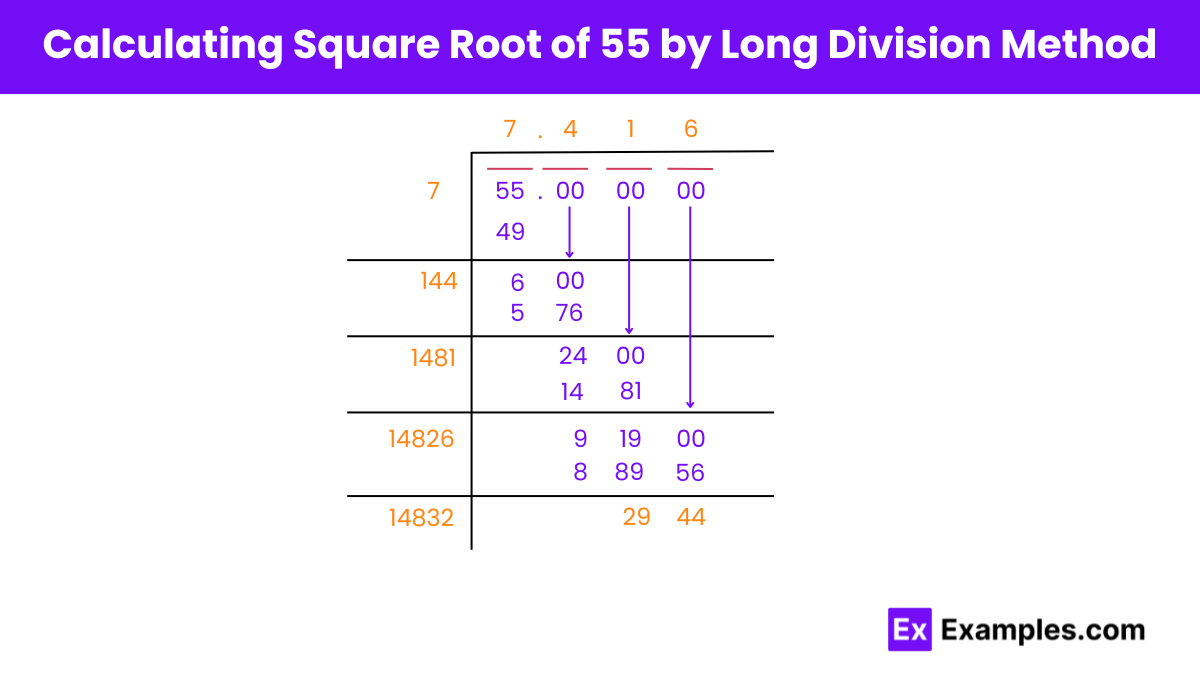
Step 1: Setup
Express 55 as 55.000000 and consider it in pairs from the right. Here, you take 55 as the initial dividend.
Step 2: Initial Division
Look for a quotient that equals the divisor such that their product is closest to but less than or equal to 55. Here, 7 × 7 = 49 is used. Subtract 49 from 55 to get the remainder 6.
Step 3: Update the Quotient
Double the quotient obtained in Step 2, which gives 2 × 7 = 14. Now, 140 becomes the new divisor.
Step 4: Refine and Extend
Place a decimal after the initial quotient (7), and bring down two zeros beside the remainder, turning it into 600 (from the remaining 6).
Step 5: Find the Next Digit
Find a digit to add to 140 and when multiplied by the resulting number, the product is less than or equal to 600. Here, 144 (140+4) × 4 = 576 works. Subtract 576 from 600 to get a remainder of 24.
Step 6: Bring Down More Zeros
Bring down the next pair of zeros, making 2400 the new dividend. Double the last complete quotient (from 74 to 148), which makes 1480 the new divisor.
Find a suitable digit to place after 148 that when squared results in 2400 or less. Here, 1481 × 1 = 1481 is used. Subtract this to get the remainder.
Step 7: Repeat if Necessary
Repeat the process by bringing down more zeros and adjusting the divisor based on the updated quotient, until the remainder reaches zero or until the desired decimal places are achieved.
The square root of 55 up to three decimal places by the long division method is thus √55 = 7.416.
No, 55 is not a perfect square. A perfect square is a number that can be expressed as the square of an integer. Since the square root of 55 is approximately 7.416, and this is not an integer, 55 does not have an integer as its square root and is therefore not a perfect square.
Can the square root of 55 be simplified?
The square root of 55 cannot be simplified into a simpler radical form because 55 is not a product of any perfect square other than 1 and itself.
How is the square root of 55 used in real life?
The square root function, including roots like that of 55, is used in various real-world applications including calculating areas, designing buildings, in physics for laws of motion and energy calculations, and in finance for various statistical models.
What are the closest perfect squares around 55?
The closest perfect squares around 55 are 49 (7^2) and 64 (8^2). These help in estimating the square root of 55 when using approximation methods.
Is there any significant pattern or property related to the square root of 55?
No specific pattern or unique property relates directly to the square root of 55 beyond its classification as an irrational number derived from a non-perfect square.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the square of 55?
3020
3025
3030
3035
Which of the following is closest to the square root of 55?
7.4
7.5
7.6
7.7
If x² = 55, what is the approximate value of x?
7.4
7.5
7.6
7.7
Simplify √55 to its decimal form.
7.43
7.44
7.45
7.46
What is (55)²?
2925
3025
3125
3225
Find the approximate value of √55 to two decimal places.
7.41
7.42
7.43
7.44
What is the square of the square root of 55?
54
55
56
57
Calculate 55 × 55.
3025
3050
3075
3100
What is the nearest integer to the square root of 55?
7
8
9
10
Which of these values is closest to √55 without using a calculator?
7.3
7.4
7.5
7.6
Before you leave, take our quick quiz to enhance your learning!

