Square & Square Root of 676
Square & Square Root of 676
Within algebraic studies, the essence of squares and square roots is pivotal. Squaring a number, like 676, entails multiplying it by itself, yielding 456976. This fundamental operation is foundational in exploring rational and irrational numbers. Rational numbers are expressed as fractions of two integers, while irrational ones evade such neat fraction expressions. Understanding these concepts enriches comprehension of mathematical relationships and patterns. From algebraic investigations to broader mathematical explorations, squares and square roots are fundamental pillars. They unveil the intricacies of numbers, paving the way for deeper insights into mathematical structures and the underlying principles governing them.
Square of 676
The square number, exemplified by the square of 676, is the result of multiplying 676 by itself, yielding 456976. In mathematics, square numbers hold significance as they exhibit properties fundamental to algebraic studies, including patterns, relationships, and foundational operations essential for broader mathematical understanding.
Square Root of 676
The square root of 676, a square number, is 26. In mathematics, square roots unravel the value of a number when multiplied by itself to yield a specific result. Understanding square roots is crucial for grasping mathematical concepts such as exponents, radicals, and the inverse relationship with squaring operations.
Square Root of 676: 26
Exponential Form: 676^½ or 23^0.5
Radical Form: √676
Is the Square Root of 676 Rational or Irrational?
The square root of 676 is rational because it equals 26, which can be expressed as a fraction of two integers (26/1). Rational numbers are those that can be expressed as a ratio of two integers, which applies to the square root of 676.
Rational Numbers:
Rational numbers are those that can be expressed as the quotient or fraction of two integers, where the denominator is not zero. In other words, they are numbers that can be represented in the form a/b, where ( a ) and ( b ) are integers and ( b ) is not zero. Examples of rational numbers include 1/2, 3/4 & 5/7. Any integer can also be expressed as a rational number by putting it over 1.
Irrational Numbers:
Irrational numbers are those that cannot be expressed as fractions and have non-repeating, non-terminating decimal representations. They cannot be expressed as the quotient of two integers. Examples of irrational numbers include (π ), ( √2} ), and ( e ). These numbers possess infinite and non-repeating decimal expansions.
Methods to Find Value of Root 676
There are several methods to find the value of the square root of 676:
Prime Factorization Method: Decompose 676 into its prime factors (2² × 13²), and then take the square root of each prime factor (2 × 13 = 26).
Long Division Method: Using long division, find the square root of 676 by iteratively guessing and refining until reaching the correct value.
Estimation Method: Approximate the square root of 676 by finding the nearest perfect squares (such as 625 and 729), then refining the estimate using trial and error or linear interpolation.
Calculator: Utilize a calculator capable of computing square roots to directly determine the value of the square root of 676.
Square Root of 676 by Long Division Method
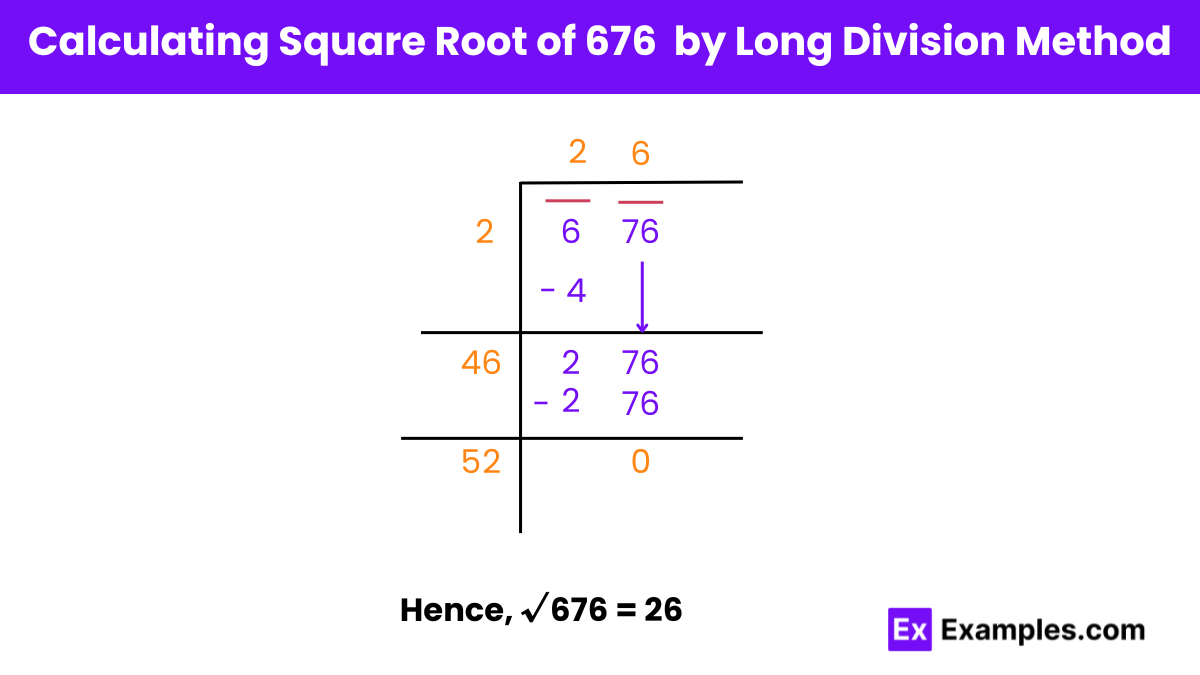
Finding the Square Root of 676 Using Long Division
Step 1: Pairing Digits
Pair digits of 676 starting from the one’s place and indicate pairing with a horizontal bar.
Step 2: Initial Estimation
Find a number whose square is less than or equal to the first pair (6). Here, 2 × 2 = 4, so the quotient is 2.
Step 3: Iterative Process
Multiply the quotient (2) by itself and subtract from the first pair (6). Bring down the next pair (00). We now have 4 as the starting digit of the new divisor.
Step 4: Refinement
Place 6 next to 4 in the divisor to create 46. Multiply the new divisor (46) by 6 and subtract from 276. The obtained answer is 0.
Step 5: Final Result
The new divisor is 52. Hence, the square root of 676 is 26.
Is 676 Perfect Square root or Not
Yes, 676 is a perfect square because its square root, which is 26, is a whole number. In mathematics, a perfect square is a number that can be expressed as the product of an integer multiplied by itself.
FAQ’S
How is the Square Root of 676 Calculated?
Various methods include prime factorization, long division, estimation, or using a calculator.
What Are Some Properties of 676 as a Perfect Square?
Its factors are easily identifiable, aiding in simplification and calculation.
What Is the Significance of the Square Root of 676?
It represents the length of one side of a square with an area of 676 square units.
Is 676 an Integer or Rational Number?
676 is both an integer and a rational number.
Are There Real-Life Applications for the Square Root of 676?
Yes, in fields like geometry, physics, and engineering, where calculating areas, distances, or quantities are involved.
Can 676 Be Represented as a Fraction?
Yes, 676 can be expressed as 676/1, making it a fraction.
What Patterns or Relationships Can Be Observed with the Square and Square Root of 676?
It follows the general relationship between squares and their square roots, exhibiting symmetry and inverse operations.
How Does Understanding the Square and Square Root of 676 Benefit Mathematical Learning?
It reinforces fundamental arithmetic principles and prepares for more advanced algebraic concepts.
Share :
