Square & Square Root of 729
Square & Square Root of 729
In the field of mathematics, particularly within algebraic studies, the fundamental concepts of squares and square roots are crucial. Squaring a number involves multiplying it by itself; for example, squaring 729 results in 531441. This operation is essential for exploring the characteristics of rational numbers, which can be expressed as a fraction of two integers, and irrational numbers, which cannot be neatly expressed as a fraction. Understanding squares and square roots deepens one’s insight into mathematical relationships and patterns, highlighting the role these operations play in the broader spectrum of algebra. Such knowledge is vital for comprehending the structure and behavior of different numerical categories in mathematics.
Square of 729
The square of 729 is a classic example of a square number in mathematics. When 729 is multiplied by itself, it produces 531,441. This operation exemplifies the concept of squaring, fundamental in algebraic studies and number theory.
Square Root of 729
The square root of 729 is a fundamental concept in mathematics, revealing how a square number can be deconstructed. Finding the square root of 729 yields 27, demonstrating how this operation inversely relates to squaring, providing insight into the symmetrical relationship between numbers.
Square Root of 729: 27
Exponential Form: 729^½ or 729^0.5
Radical Form: √729
Is the Square Root of 729 Rational or Irrational?
The square root of 729 is a rational number because it equals 27, which can be expressed as the ratio of two integers (27/1). Rational numbers are those that can be expressed as the quotient or fraction of two integers, where the denominator is not zero. In this case, since 729 is a perfect square (27 × 27 = 729), its square root is a whole number, making it a rational number.
Rational numbers : Rational numbers are those that can be expressed as the ratio of two integers, with a non-zero denominator. They take the form a/b, where a and b are integers and b ≠ 0. Examples include integers like -3, fractions such as 1/2, and mixed numbers like 5/7.
Irrational numbers : Irrational numbers cannot be represented as fractions of integers and have decimal representations that neither repeat nor terminate. Examples include the square roots of non-perfect squares like √2, √3, and √5, as well as transcendental numbers like π.
Methods to Find Value of Root 729
There are several methods to find the value of the square root of 729:
Prime Factorization Method: Express 729 as the product of its prime factors: (3⁶). Since the square root of a number involves taking one-half of the exponent of each prime factor, the square root of (3⁶) is (3⁶/²} = 3³ = 27).
Repeated Subtraction or Guess and Check Method: Start with a guess, say 20. Square it to get 400, which is less than 729. Increase the guess. Try 25. Squaring it gives 625, which is still less than 729. Increase the guess again. Try 30. Squaring it gives 900, which is more than 729. So, we know the square root is somewhere between 25 and 30. Continue refining the guess until you find the closest value. In this case, the square root is 27.
Using a Calculator or Computer: Most calculators and computers have built-in functions to calculate square roots. Simply input 729 and find the square root.
Long Division Method: This method involves a bit of division algorithm and is less commonly used, but it’s still a valid way to find the square root of a number manually.
Choose the method that best suits your preferences or requirements.
Square Root of 729 by Long Division Method
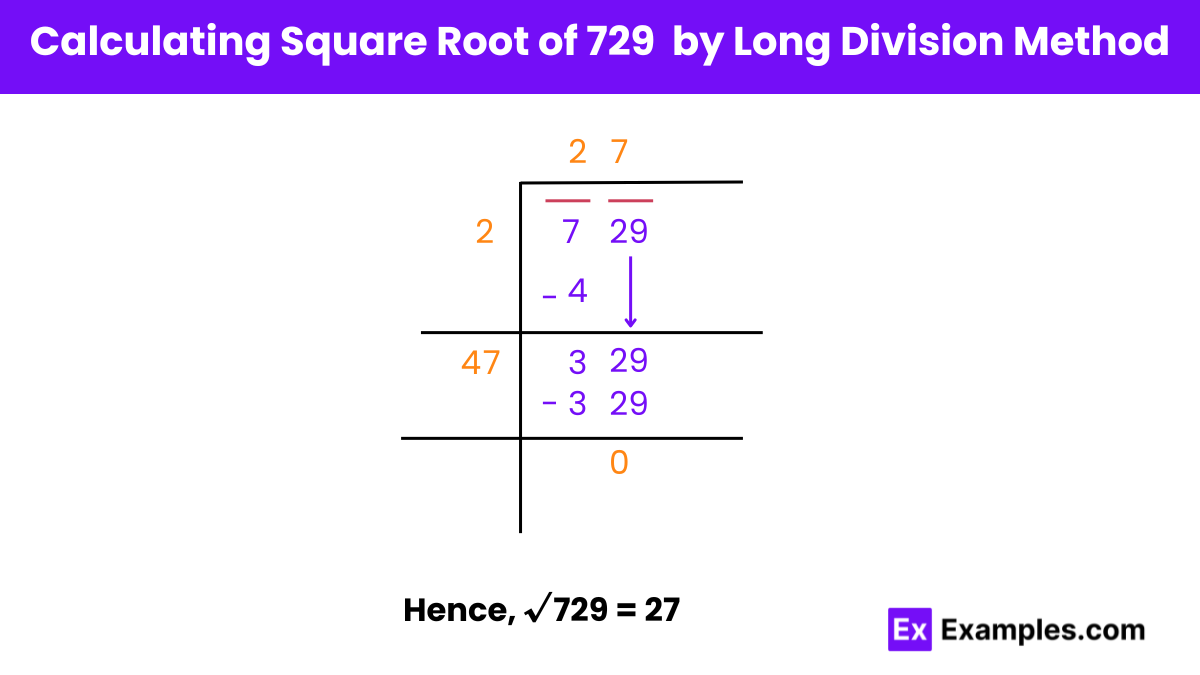
Square Root of 729 Using Long Division Method
Step 1: Setting Up
Write down 729 and pair the digits from the right in groups of two.
In this case, we have two pairs: 7 and 29.
Step 2: Finding the First Digit
Determine a number (n) such that n × n is less than or equal to 7.
In this case, n = 2, as 2 × 2 = 4.
Step 3: Division
Subtract the square of the obtained digit (4) from the first pair (7).
Add the digit (2) with itself (2 + 2 = 4).
Bring down the second pair (29), forming the new dividend.
The remainder after this step is 329.
Step 4: Finding the Next Digit
Find a number (m) such that 2m × m is less than or equal to 329.
Here, m = 7, as 47 × 7 = 329.
By following these steps, you can continue the long division process to find the square root of 729.
Is 729 Perfect Square root or Not
Yes, 729 is a perfect square. It can be expressed as the square of an integer, specifically (27²). So, the square root of 729 is indeed a whole number, which is 27.
FAQ’S
Is 729 a composite number?
Yes, 729 is a composite number because it has factors other than 1 and itself. Its factors include 1, 3, 9, 27, 81, 243, and 729.
What does it mean if the square root of a number is a whole number?
If the square root of a number is a whole number, it means that the original number is a perfect square.
How can I check if 729 is a perfect square without calculation?
You can check if 729 is a perfect square by looking for the repeated pairs of prime factors. Since 729 can be expressed as 3636, and 6 is even, 729 is a perfect square.
Share :
