Which of the following is not a square root of 74?
8.60
8.7
8.5
9
of 10
Square & Square Root of 74 – Methods, Calculation, How to find
Square & Square Root of 74 – Methods, Calculation, How to find
In mathematics, particularly within algebra, squares and square roots are foundational. Squaring a number like 74 involves multiplying it by itself to obtain 5476, which is fundamental for exploring rational and irrational numbers. Understanding these concepts enriches comprehension of mathematical relationships and patterns, vital in algebraic studies and beyond.
Square of 74
A square number, such as 74, results from multiplying an integer by itself. The square of 74 equals 5476. This fundamental operation illustrates algebraic principles, showcasing the properties of rational and irrational numbers, enriching understanding of mathematical relationships and patterns.
Square Root of 74
Or
√74 ≈ 8.602 Up to 3 decimals
The square root of 74, when squared, equals 74. It’s the number that, when multiplied by itself, gives 74. The square root, approximately 8.602, unveils the origin of 74. Understanding square roots elucidates their role in algebraic analysis, showcasing their significance in mathematical patterns and relationships.
Exponential Form : 74^½ or 74^0.5
Radical Form : √74
Is the Square Root of 74 Rational or Irrational?
This is because it cannot be expressed as a fraction of two integers, and its decimal representation goes on indefinitely without repeating or terminating.
Rational Numbers: Expressible as fractions of two integers, like 3/4 or -5/2.
Irrational Numbers: Cannot be written as fractions of integers. Their decimal expansions neither terminate nor repeat. For example, √2 ≈ 1.41421356 is irrational.
Methods to Find Value of Root 74
Estimation Method: Make an initial guess, then refine it iteratively using approximation techniques.
Prime Factorization Method: Express 74 as a product of prime factors, then find the square root of each prime factor.
Long Division Method: Apply long division to iteratively find the digits of the square root.
Using Calculator: Use a calculator with a square root function to directly compute the square root of 74.
Square Root of 74 by Long Division Method
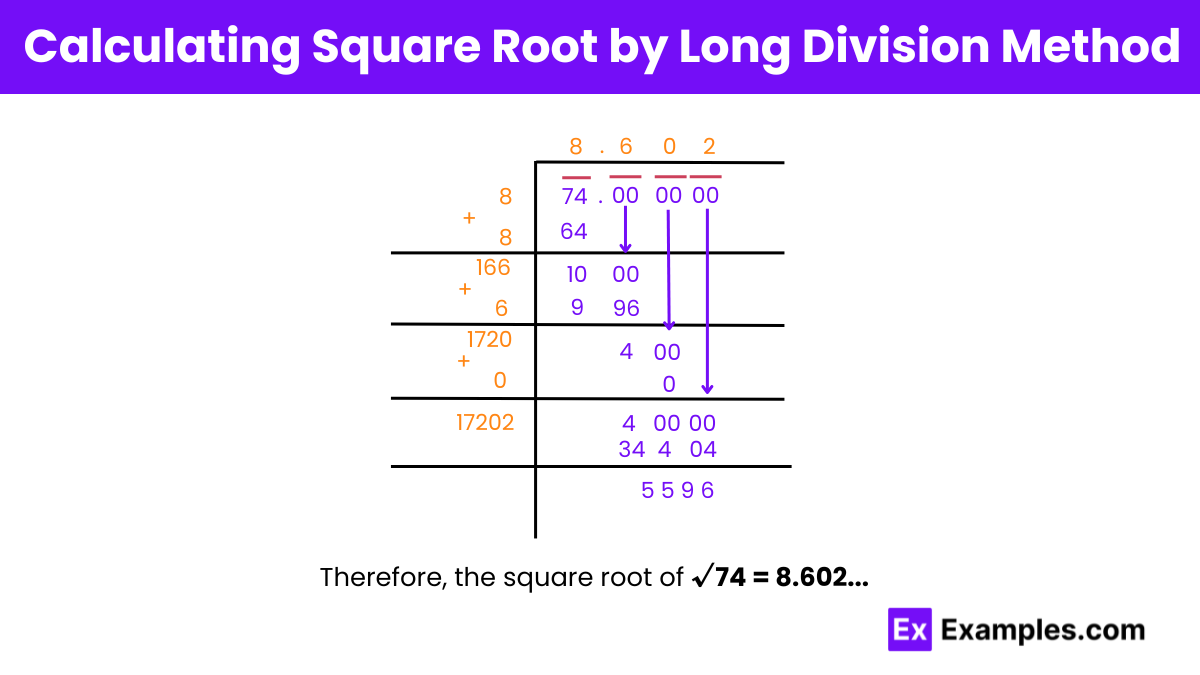
Step 1: Digit Pairing
- Pair the digits of 74 starting from the right, indicating with a horizontal bar. We have one pair: 74.
- Since there are no more pairs, we can consider adding decimal points and pairs of zeros for further precision.
Step 2: Initial Quotient
- Find a number whose square is less than or equal to the first paired digits (74). The closest perfect square less than 74 is 64, which is 8².
- Place 8 as the initial quotient and divisor, and subtract 64 from 74, which gives the remainder 10.
Step 3: Bring Down the Next Pair of Digits
- Bring down a pair of zeros next to the remainder (10), making it 1000.
- Double the initial divisor (8), resulting in 16. Place it to the left with a blank space next to it to form the new divisor (16).
Step 4: Determine the Next Digit
- Find a digit to place in the blank space such that when the new divisor is multiplied by this digit, the product is less than or equal to 1000. The digit is 6, forming the new divisor 166.
- Multiply 166 by 6, which equals 996. Subtract this from 1000, giving the remainder 4.
Step 5: Bring Down More Zeros
- Bring down the next pair of zeros, making the new dividend 400.
- Double the previous quotient (86) to get 172. Add a blank space next to it to form the new divisor (172_).
Step 6: Determine the Next Digit
- Find a digit to place in the blank space such that when the new divisor is multiplied by this digit, the product is less than or equal to 400. The digit is 0, forming the new divisor 1720.
- Multiply 1720 by 0, which equals 0. Subtract this from 400, giving the remainder 400.
Step 7: Continue the Process
- Continue bringing down pairs of zeros and repeating the steps to refine the quotient.
- Next, bring down a pair of zeros making the new dividend 40000.
- The next digit to place in the blank space is 2, forming the new divisor 17202.
- Multiply 17202 by 2, which equals 34404. Subtract this from 40000, giving the remainder 5596.
Final Result
- Continue the process as needed for desired precision. The quotient so far is approximately 8.602.
- Therefore, √74 ≈ 8.602.
Decimal point and adding zeros in pairs to the remainder until the desired accuracy is achieved.
Is 74 a Perfect Square?
74 is not a perfect square because it cannot be expressed as the product of an integer multiplied by itself. There are no integers where the product of the integer with itself equals 74.
What is the square root of 74 to the nearest tenth?
The square root of 74 to the nearest tenth is approximately 8.6. This value is derived from the long division method, refining the result to one decimal place.
What are the factors of 74?
The factors of 74 are 1, 2, 37, and 74. These numbers divide 74 without leaving a remainder, showing its divisibility properties.
Why is 74 a prime number?
74 is not a prime number because it has more than two distinct positive divisors: 1, 2, 37, and 74. Prime numbers have exactly two distinct positive divisors.
Share :
Practice Test
What is the nearest perfect square to 74?
64
81
49
100
of 10
If the square of a number is 74, what is the number?
8.5
8.60
8.7
9
of 10
The value of √74 falls between which two consecutive integers?
8 and 9
9 and 10
7 and 8
10 and 11
of 10
What is the square of 9?
81
74
100
64
of 10
Which number squared is just above 74?
8
9
10
11
of 10
If x² = 74, what is the value of x?
8.5
8.60
8.7
9
of 10
What is the value of √74 in decimal form rounded to two decimal places?
8.60
8.66
8.70
8.75
of 10
The square of which of the following is closest to 74?
8
9
10
11
of 10
What is the square root of 5476?
73
74
75
76
of 10