What is the square of 78?
6084
6086
6088
6090
of 10
Square & Square Root of 78 – Methods, Calculation, How to find
Square & Square Root of 78 – Methods, Calculation, How to find
In the realm of mathematics, particularly within algebra, the importance of squares and square roots cannot be overstated. These concepts are fundamental, shaping our understanding of rational and irrational numbers.
Square of 78
A square number, like 78, arises from multiplying an integer by itself. The square of 78 equals 6,084, showcasing algebraic principles and enriching mathematical comprehension.
Square Root of 78
Or
√78 ≈ 8.831 Upto 3 decimals
The square root of 78, though irrational, enriches our understanding of algebraic relationships and patterns. Mastering square roots involves identifying the number whose square equals 78.
Exponential Form: 78^½ or 78^0.5
Radical Form: √78
Is the Square Root of 78 Rational or Irrational?
Rational Numbers: Expressible as fractions of two integers.
Irrational Numbers: Cannot be expressed as fractions of integers.
As the square root of 78 is not a perfect square, it is irrational.
Methods to Find the Value of Root 78:
Estimation Method: Iterative refinement of initial approximations.
Prime Factorization Method: Express 78 as a product of prime factors.
Calculator: Utilize a calculator with a square root function.
Square Root of 78 by Long Division Method:
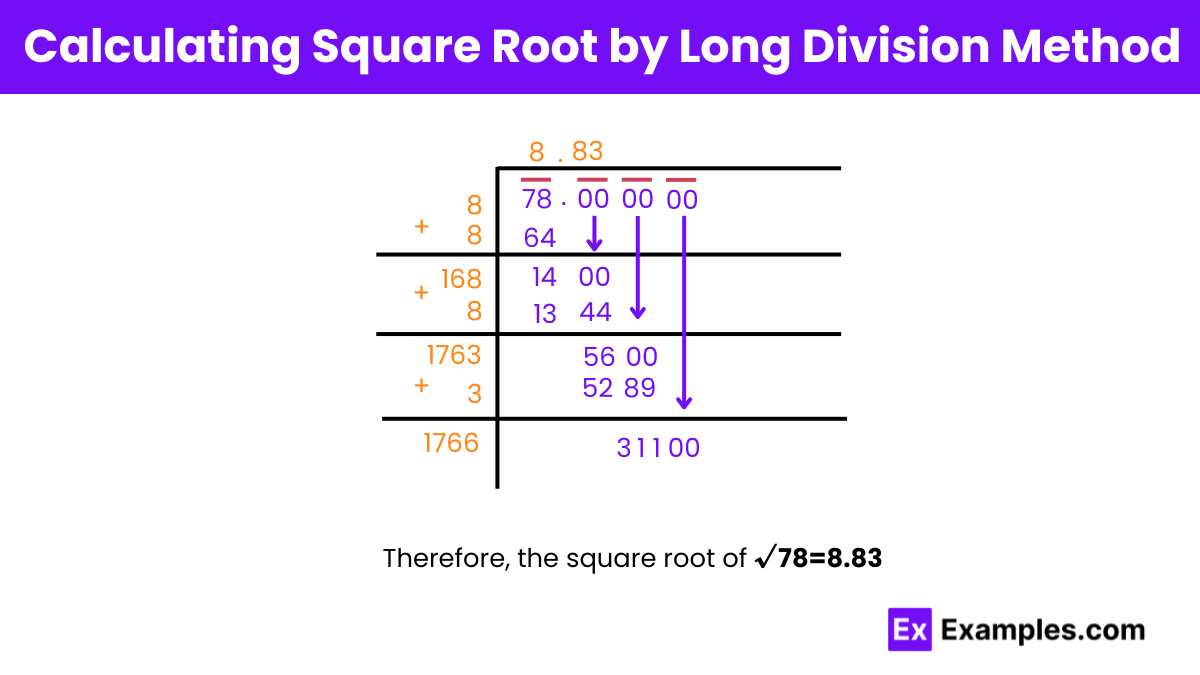
Step 1: Identify perfect squares around 78. 8^2 = 64 < 78 and 9^2 = 81 > 78.
Step 2: Inequality: 8 < √78 < 9, representing 64 < 78 < 81.
Step 3: Transform to square roots: √6400 < √7800 < √8100.
Step 4: Refine inequality: √7744 < √7800 < √7921. 88 < 10√78 < 89.
Step 5: Average the limits: (8.8 + 8.9)/2 = 8.85.
Thus, √78 ≈ 8.85.
78 is a Perfect Square or Not
Perfect square cannot be expressed as the product of an integer multiplied by itself.
FAQs
Which number is closest to √ 78?
The number closest to √78 is 9, as √78 is approximately 8.83176. Since 9 is the nearest whole number, it provides the closest approximation.
Can the square root of 78 be simplified further?
No, the square root of 78 is already in its simplest form.
How does √78 relate to Pythagorean triples?
√78 does not directly relate to Pythagorean triples since 78 is not a perfect square.
Share :
Practice Test
Which of these numbers is closest to the square root of 78?
8.7
8.8
8.9
9.0
of 10
If y² = 78, what is y approximately equal to?
8.6
8.7
8.9
8.8
of 10
What is the square root of 78 rounded to the nearest tenth?
8.7
8.8
8.9
9
of 10
Calculate 78².
6084
6086
6090
6096
of 10
Find the approximate value of √78.
8.8
8.9
9.0
9.1
of 10
Determine the integer part of √78.
8
9
10
11
of 10
What is 78 raised to the power of 0.5?
8.8
8.9
9
1
of 10
Which value is not a square but is closest to 78?
64
72
81
84
of 10
Which number is the best estimate for √78?
8.7
8.8
8.9
9.0
of 10