What is the square of 90?
8100
8200
8300
8400
of 10
Square & Square Root of 8100 – Methods, Calculation, How to find
Square & Square Root of 8100 – Methods, Calculation, How to find
In the realm of mathematics, particularly within algebra, the significance of squares and square roots cannot be overstated. These concepts form the bedrock upon which our understanding of rational and irrational numbers is built. By taking a number like 8100 and squaring it, we illustrate the fundamental nature of this operation, paving the way for deeper exploration of mathematical relationships and patterns.
Square of 8100
A square number such as 8100, arises from multiplying an integer by itself. The square of 8100 equals 65,610,000, highlighting algebraic principles and enriching comprehension of mathematical relationships and patterns within algebraic studies and beyond.
Square Root of 8100
The square root of 8100, a perfect square number, is 90. Mastery of square roots involves identifying the number that, when multiplied by itself, equals 8100. This understanding is crucial for exploring algebraic relationships and patterns within mathematics.
Exponential Form: 8100^½ or 8100^0.5
Radical Form: √8100
Is the Square Root of 8100 Rational or Irrational?
Rational Numbers: Rational numbers are expressible as fractions of two integers.
Irrational Numbers: Irrational numbers cannot be expressed as fractions of integers.
As the square root of 8100 is a perfect square, it is rational. It can be expressed as the fraction 90/1.
Methods to Find the Value of Root 8100
Estimation Method: Begin with an initial approximation and refine it iteratively using methods like Newton-Raphson.
Prime Factorization Method: Express 8100 as a product of prime factors, then find the square root of each prime factor.
Calculator: Utilize a calculator with a square root function to directly compute the square root of 8100.
Square Root of 8100 by Long Division Method
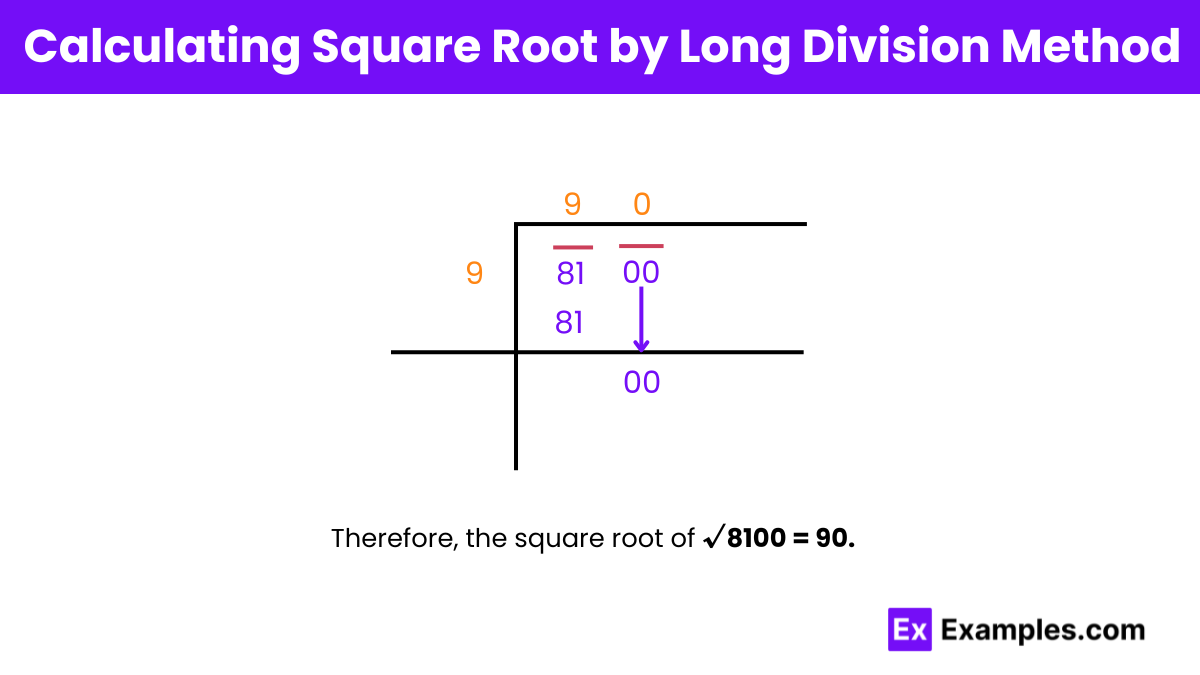
Step 1: Pairing Digits
Pair the digits of 8100, yielding 81 and 00.
Step 2: Finding Y
Find a number Y (9) such that its square is less than or equal to 81. Divide 81 by 9, yielding a quotient of 9.
Step 3: Bringing Down
Bring down the next pair of digits (00), forming a new dividend of 0.
Step 4: Constructing the Divisor
Add the last digit of the quotient (9) to the divisor (9), resulting in 18. Find a digit Z (0) such that when appended to 18, the product is less than or equal to the new dividend (0). Thus, 0 is found, creating a new divisor of 180.
Step 5: Continued Division
Divide the new dividend (0) by the new divisor (180), resulting in a quotient of 0 and a remainder of 0.
Step 6: Conclusion
Since the remainder is now 0 and there are no more digits to bring down, we conclude the process. Therefore, the square root of 8100 by the long division method is 90.
8100 is a Perfect Square or Not
8100 is a perfect square because it can be expressed as the product of an integer multiplied by itself. In this case, 90 × 90 = 8100, indicating that 8100 is indeed a perfect square.
What is the prime factorization of 8100 using exponents?
The prime factorization of 8100 using exponents is ( 2² × 3⁴ × 5² ).
What are the factors of 8100?
The factors of 8100 are all the numbers that can divide evenly into 8100 without leaving a remainder. They include: 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 25, 27, 30, 36, 45, 50, 54, 60, 75, 90, 100, 108, 135, 150, 180, 225, 270, 300, 450, 540, 675, 900, 1350, 1620, 2025, 2700, and 4050.
What is 8100 as a product of prime numbers?
8100 as a product of prime numbers is ( 2² × 3⁴ × 5² ).
How many divisors does 8100 have?
8100 has 36 divisors because it can be factored into ( 2² × 3⁴ × 5² ), and the number of divisors can be calculated using the exponents.
Share :
Practice Test
What is the square root of 8100?
80
85
90
95
of 10
Which of the following numbers is closest to the square root of 8100?
89
90
91
92
of 10
What is the approximate square root of 8100 to the nearest whole number?
89
90
91
92
of 10
The square of which of the following is closest to 8100?
85
90
91
92
of 10
What is the value of √8100 in decimal form?
90
89.5
90.5
91
of 10
If x² = 8100, what is the value of ?
85
90
95
100
of 10
Which number squared is just above 8100?
90
91
92
93
of 10
The value of √8100 falls between which two consecutive integers?
89 and 90
90 and 91
91 and 92
88 and 89
of 10
If the square of a number is 8100, what is the number?
89
90
91
92
of 10