Square Pyramid – Examples, Definition, Formula, Properties, Types

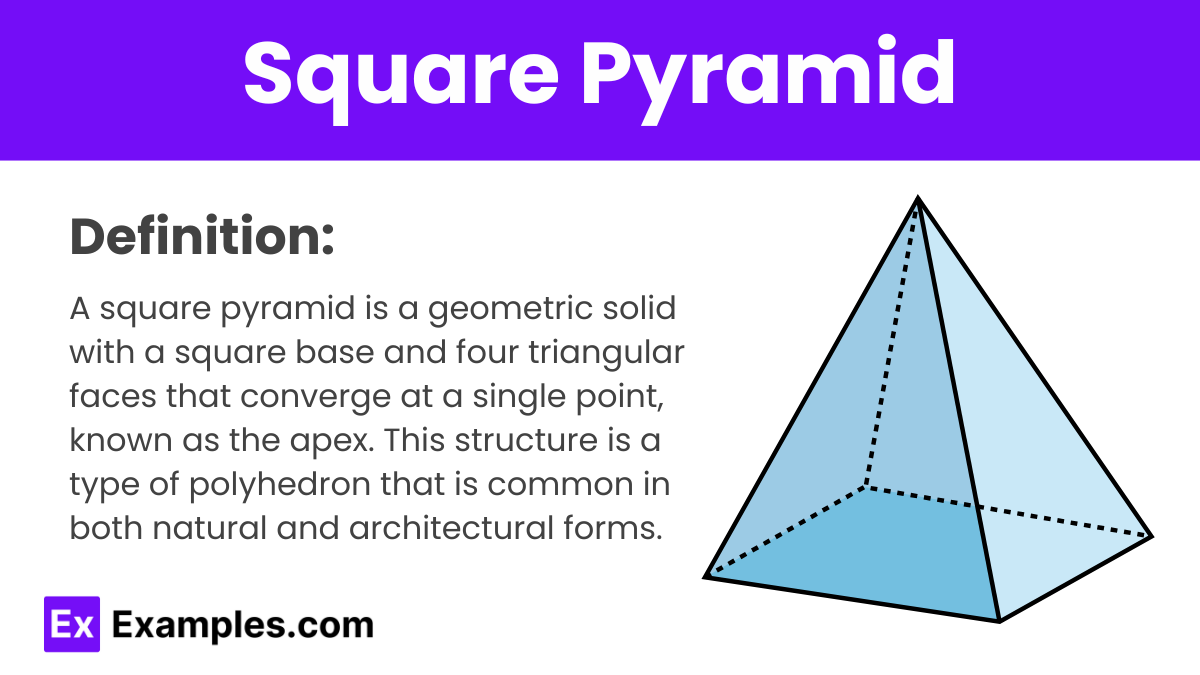
A square pyramid is a three-dimensional geometric figure with a square base and four triangular faces converging at a point called the apex. In mathematics, this shape can be analyzed using algebra to explore its properties, such as volume and surface area. Concepts like square and square roots are vital in calculating these dimensions, especially when dealing with the pyramid’s height or slant height. Additionally, the least squares method, a statistical tool, may be used to optimize real-world pyramid constructions or models involving integers, rational, and irrational numbers. This integration of geometry with other mathematical disciplines like statistics and number theory highlights the interconnected nature of mathematical concepts. and the pyramids are Called after their base, such as

• Rectangular pyramid
• Triangular pyramid
• Square pyramid
• Pentagonal pyramid
• Hexagonal pyramid

What is a Square Pyramid?

Square Pyramid Formula

A square pyramid, characterized by a square base and triangular sides that meet at an apex, is a fundamental shape in geometry. Understanding how to calculate its volume and surface area involves specific formulas. Here are the key formulas used for a square pyramid:

Volume of a Square Pyramid

The volume 𝑉 of a square pyramid is calculated by the formula:

Where:

• Base Area is the area of the square base and can be calculated as 𝑠² (where 𝑠s is the length of a side of the square).
• Height (ℎ) is the perpendicular distance from the base to the apex.

Expressed with base side and height, the formula becomes: 𝑉 = 1/3𝑠²ℎ

Surface Area of a Square Pyramid

The surface area 𝐴 of a square pyramid is the sum of the area of the base and the area of the triangular sides. The formula is:

Where:

• 𝑠 is the length of a side of the square base.
• ℎ is the slant height of the pyramid, not the vertical height. The slant height can be calculated using the Pythagorean theorem if not provided, using the relation Slant Height = √(𝑠/2)²+ℎ²​.

Lateral Surface Area of a Square Pyramid

The lateral surface area is the total area of just the triangular sides and is calculated without including the base:

This formula helps in finding the area of the material needed if the base is not covered.

Properties of a Square Pyramid

• Base: The foundation of the square pyramid is a square, meaning all four sides are equal in length.
• Faces: Aside from the square base, the pyramid has four triangular faces. Each triangle shares one side with the square base and the other two sides meet at the apex.
• Vertex: The apex or vertex is the common point at the top where all triangular faces converge.
• Edges: A square pyramid has eight edges—four edges of the base and four edges that are the sides of the triangles leading to the apex.
• Symmetry: The pyramid has a vertical line of symmetry that passes through the apex and the center of the base.

Examples of Square Pyramid Formulas

Example 1: Calculating the Volume of a Square Pyramid

Problem: Find the volume of a square pyramid with a base side length of 4 meters and a perpendicular height from the base to the apex of 9 meters.

Solution:

• Base side length (𝑠): 4 m
• Height (h): 9 m

Using the formula for the volume of a square pyramid: 𝑉=1/3𝑠²ℎ.

Substitute the given values:

• 𝑉=1/3×(4)²×9
• 𝑉=1/3×16×9
• 𝑉=1/3×144
• 𝑉=48 cubic meters.

Answer: The volume of the pyramid is 48 cubic meters.

Example 2: Calculating the Surface Area of a Square Pyramid

Problem: Calculate the surface area of a square pyramid with a base side length of 3 meters and a perpendicular height of 6 meters.

Solution:

• Base side length (𝑠): 3 m
• Perpendicular height (ℎ): 6 m

First, calculate the slant height (𝑙) using the Pythagorean theorem (since the slant height is the hypotenuse of the triangle formed by the half of the base and the height):

• 𝑙 = √(𝑠/2)²+ℎ²
• 𝑙 = √(3/2)²+6²
• 𝑙 = √2.25+36
• 𝑙 = √38.25
• 𝑙 = 6.18 metersl≈6.18 meters

Now, use the surface area formula:

• 𝐴 = 𝑠²+2𝑠×𝑙
• 𝐴 = 3²+2×3×6.18
• 𝐴 = 9+37.08
• 𝐴 = 46.08 square meters.

The surface area of the pyramid is approximately 46.08 square meters.

Example 3: Calculating the Lateral Surface Area of a Square Pyramid

Problem

Calculate the lateral surface area of a square pyramid with a base side length of 5 meters and a vertical height (from the base to the apex) of 12 meters.

Solution

Given:

• Base side length (𝑠): 5 m
• Vertical height (ℎ): 12 m

First, we need to determine the slant height (𝑙), which is necessary for calculating the lateral surface area. The slant height can be found using the Pythagorean theorem in the right triangle formed by half the side of the base, the vertical height, and the slant height itself.

Step 1: Calculate the Slant Height

• 𝑙 = √(𝑠/2)²+ℎ²
• 𝑙 = √(5/2)²2+12²
• 𝑙 = √2.5²+12²
• 𝑙 = √6.25+144
• 𝑙 = √150.25
• 𝑙 = 12.26 meters.

Step 2: Calculate the Lateral Surface Area

The formula for the lateral surface area is:

• Lateral Surface Area = 2𝑠×𝑙
• Lateral Surface Area = 2×5×12.26
• Lateral Surface Area = 10×12.26
• Lateral Surface Area = 122.6 square meters.

The lateral surface area of the square pyramid is approximately 122.6 square meters. This calculation shows how the geometry of the pyramid and basic trigonometry come together to solve practical problems involving real-world objects.

Types of Square Pyramids

Square pyramids can be classified based on their symmetry, the orientation of their apex, and the relative lengths of their edges. Understanding these types helps in applications ranging from architectural design to geometric analysis. Here are the main types of square pyramids:

Regular Square Pyramid

• A regular square pyramid has a square base and four congruent triangular faces.
• The apex (top vertex) is directly above the center of the base, making the line from the apex to the base’s center perpendicular to the base. This symmetry ensures that all the triangular faces are isosceles.

Right Square Pyramid

• Often used interchangeably with a regular square pyramid, a right square pyramid is defined primarily by the perpendicular line from its apex to the center of the base.
• It maintains symmetrical properties, with the apex aligned directly over the geometric center of the base.

Oblique Square Pyramid

• Unlike the regular or right square pyramid, an oblique square pyramid has an apex that is not perpendicularly above the center of the base.
• The triangular faces are not congruent in this pyramid, and the apex is offset, which results in two triangular faces being larger than the other two.

Truncated Square Pyramid

• A truncated square pyramid, or a frustum of a pyramid, results when a square pyramid is sliced parallel to the base, cutting off the apex.
• This type retains a square base, but the top is also a square, albeit smaller than the base. The sides are trapezoidal.

Net of a Square Pyramid

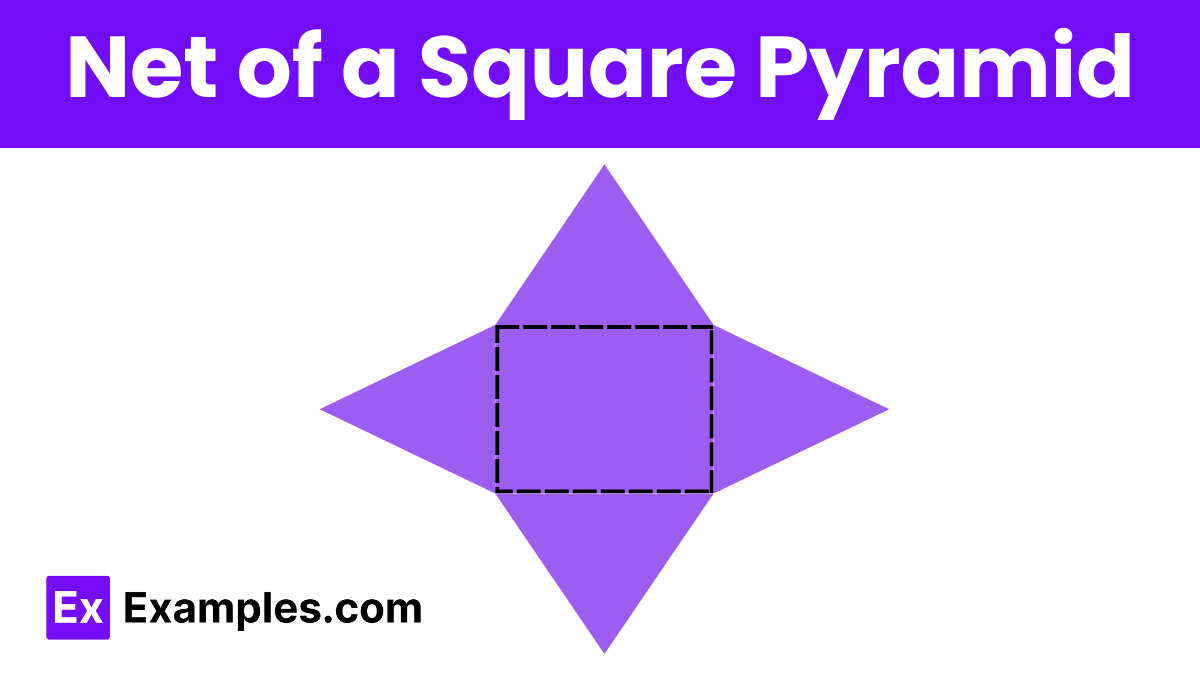
A net of a square pyramid is a two-dimensional representation that can be folded to form the three-dimensional shape of the pyramid. Understanding the net of a square pyramid helps visualize how the sides fit together and is particularly useful in educational contexts for teaching geometry, as well as in practical applications like crafting and architecture.

Components of the Net

The net of a square pyramid consists of the following components:

One Square:

• This represents the base of the pyramid.
• All four sides are of equal length.

Four Congruent Triangles:

• These triangles represent the lateral faces of the pyramid.
• Each triangle has a base that is equal in length to a side of the square and two sides that meet at the apex of the pyramid.

Notes on Square Pyramids

Square pyramids, often studied in geometry and applied in various real-world contexts, have several key characteristics and properties that are crucial for understanding their structure and function. Here are some important notes on square pyramids:

Mathematical Properties

• Volume: The volume of a square pyramid can be calculated using the formula 𝑉 = 1/3𝑠²ℎ, where 𝑠s is the length of a side of the base, and ℎ is the height from the base to the apex.
• Surface Area: The total surface area includes the area of the base and the lateral surface area. It is calculated with 𝐴 = 𝑠²+2𝑠√(𝑠/2)²+ℎ²​, where ℎ is the slant height.
• Symmetry: Regular square pyramids have a symmetrical structure about the vertical axis passing through the apex and the center of the base.

Practical Applications

• Architecture: Square pyramids are prominent in architectural designs, notably seen in ancient monuments like the Egyptian pyramids.
• Engineering: Understanding the properties of square pyramids can help in designing roofs, supports, and other structural elements.

Educational Significance

• Geometric Understanding: Studying square pyramids aids in comprehending more complex geometric and three-dimensional shapes.
• Problem Solving: Calculating areas and volumes of square pyramids integrates the use of algebra and trigonometry, enhancing problem-solving skills.

Crafting and Model Making

• Nets: Creating a net for a square pyramid (a flat layout of the base and triangular sides) is a useful exercise in visualizing and understanding three-dimensional shapes.

Challenges in Computation

• Precision: Calculating the slant height and other derived measurements require precision, especially in a mathematical or engineering context, to ensure accuracy in computations.

FAQs

How do square pyramids contribute to learning geometry?

Studying square pyramids helps students understand concepts of volume, surface area, and three-dimensional shape structure, enhancing spatial awareness and geometric visualization skills.

Are square pyramids only used in mathematical contexts?

No, square pyramids are used in various fields besides mathematics, including architecture, engineering, and education. They serve as practical examples of geometric principles and are also aesthetically pleasing structures.

What is the difference between a regular and an oblique square pyramid?

A regular square pyramid has its apex directly above the center of the base and is symmetrical, while an oblique square pyramid has an apex that is not aligned above the center of the base, causing the sides to be asymmetrical.