Algebra Expressions and Equations

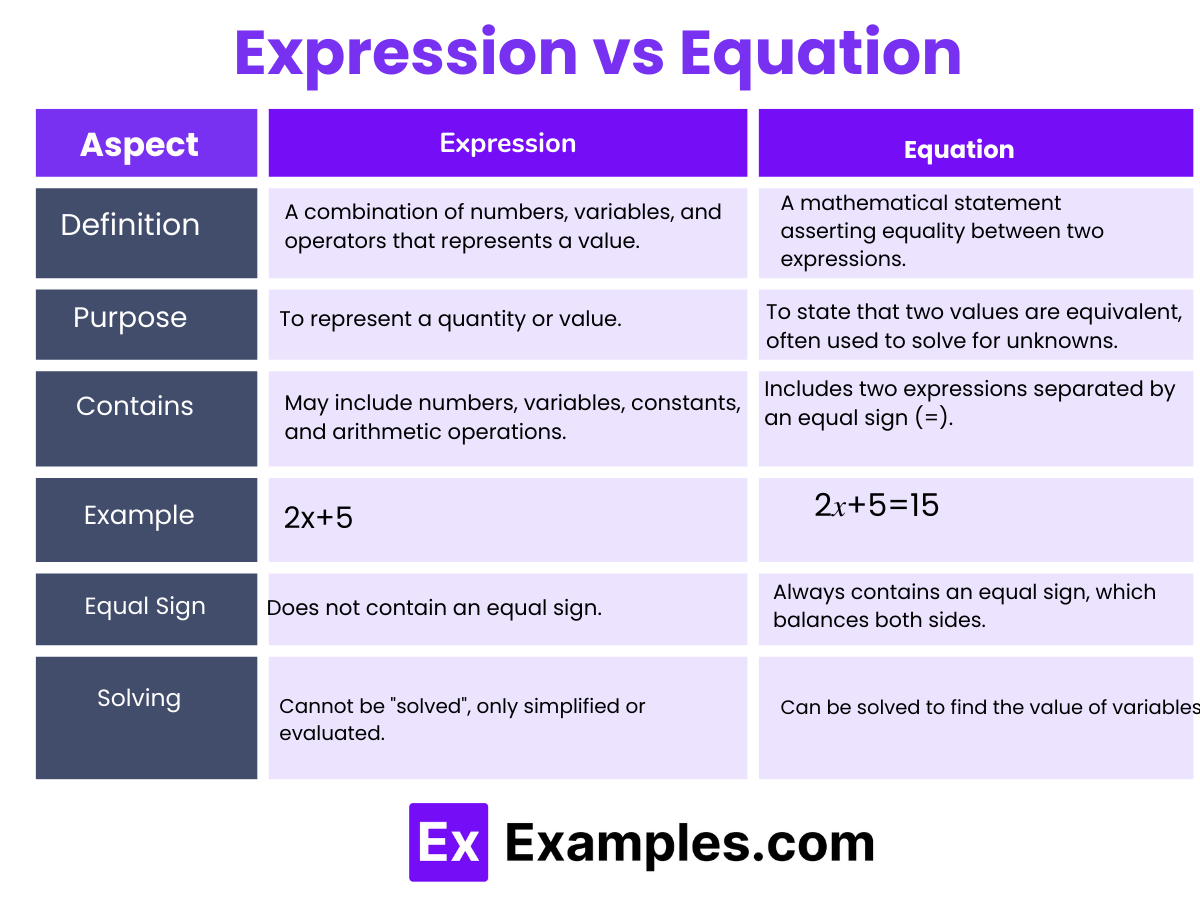
Algebra is a fundamental branch of mathematics that explores the relationships between variables and constants through expressions and equations. Algebra expressions consist of terms combined using operations like addition, subtraction, multiplication, and division, often containing variables that represent unknown values. Equations, on the other hand, set two expressions equal to each other, forming the basis for solving problems by finding the values of these variables. This field is essential in developing critical thinking and problem-solving skills, applicable in various real-world contexts from engineering to economics. Understanding how to manipulate and solve these algebraic expressions and equations is crucial for students and professionals alike

What are Algebra Expressions And Equations ?

In mathematics, particularly in algebra, the terms “expressions” and “equations” play fundamental roles and serve different functions within problem-solving contexts. Understanding each and their relationship can greatly enhance your ability to manipulate and solve algebraic problems. Here’s a breakdown:

Algebraic Expressions

An algebraic expression is a combination of variables, numbers, and operations (such as addition, subtraction, multiplication, and division). Expressions do not contain equal signs; instead, they represent values that can be simplified but not solved. For example, the expression 2x+5 combines the variable xxx with numbers through multiplication and addition. Algebraic expressions can be as simple as a single term, like 5x5x5x, or more complex with multiple terms, like 3x²−4x+7

Algebraic Equations

An algebraic equation, on the other hand, is a statement that asserts the equality of two expressions, featuring an equal sign (=). Equations are solvable, meaning you can manipulate them to find the value(s) of the variable(s) that make the equation true. For instance, the equation 2x+5=15 can be solved by finding the value of x that balances both sides of the equal sign.

Relationship and Use

Both algebraic expressions and equations are used to describe relationships between quantities and to solve problems. Expressions can be part of equations; they can be evaluated given certain values, simplified, or even transformed into equations by including an equality to another expression. Equations can be solved to find unknown values, analyzed, and applied in various practical scenarios like physics, engineering, and economics.

Difference between Algebraic Expression and Equation

How to Solve Algebraic Equations?

Solving algebraic equations is a systematic process that involves manipulating the equation to isolate the variable and simplify the expression. Here’s a step-by-step guide on how to approach solving algebraic equations:

Simplify Both Sides: Start by simplifying both sides of the equation. Combine like terms and simplify any algebraic expressions.

Isolate the Variable: Use addition or subtraction to move terms that contain the variable to one side of the equation and all constant terms to the other side.

Undo Multiplication or Division: If the variable is multiplied by a coefficient or divided, use the opposite operation to isolate the variable. For multiplication, divide both sides by the same number, and for division, multiply both sides.

Check for More Solutions: Some equations, like quadratic equations, may have more than one solution. Be sure to explore all potential solutions.

Verify Your Solution: Substitute the solution back into the original equation to verify that it works. This step ensures that the solution is correct and that no errors were made during the process.

Consider Special Cases: Be aware of special cases, such as no solution (when the equation simplifies to a contradiction, like 3=23) or infinite solutions (when the equation simplifies to a tautology, like 0=00).

Algebraic Expression and Equation Problem

Algebraic expressions and equations form the backbone of algebra, each serving a specific purpose in mathematical problem-solving. Understanding the distinction between them and how to handle each is crucial in mastering algebra.

Algebraic Expression

An algebraic expression is a combination of variables, numbers, and arithmetic operations (such as addition, subtraction, multiplication, and division). It does not include an equality sign, so it cannot be solved but can be simplified. Expressions are used to represent values and can be part of broader mathematical formulas or functions.

Purpose: To represent relationships or formulas involving variables without asserting equality.

Algebraic Equation

An algebraic equation, on the other hand, involves variables and numbers connected by arithmetic operations, but crucially, it includes an equality sign. This equality defines a problem that needs solving: finding the value(s) of the variables that make the equation true.

Purpose: To solve for unknown values, usually represented by variables, that satisfy the equality condition set by the equation.

Problem-Solving Approach for Algebraic Expressions and Equations

Expressions:

1. Simplify: Combine like terms (terms that have the same variables raised to the same power).
2. Evaluate: Substitute known values for variables if required and simplify further to find the value of the expression.

Equations:

1. Simplify Both Sides: Simplify each side of the equation separately by combining like terms and using the distributive property if necessary.
2. Isolate the Variable: Move all terms containing the variable to one side and all constant terms to the other side using basic arithmetic operations.
3. Solve for the Variable: Use inverse operations to isolate the variable completely. For instance, if the variable is multiplied by a number, divide both sides by that number.
4. Check Your Solution: Substitute the solution back into the original equation to verify accuracy.

Example Problem

To illustrate, consider an equation and an expression:

• Expression: 3x+5
• Equation: 3x+5=11

For the expression, you might be asked to simplify or evaluate it for a specific value of x. For the equation, you would solve it to find the value of xxx that makes it true. Solving 3x+5=11 involves isolating x by first subtracting 5 from both sides, resulting in 3x=6, and then dividing both sides by 3 to find x=2

How to Simplify Algebraic Expressions?

Step 1: Remove Parentheses

Start by expanding the expression, using the distributive property to eliminate parentheses. Multiply each term inside the parentheses by the term outside, if applicable.

Example: a(b+c)=ab+ac

Step 2: Combine Like Terms

Like terms are terms that contain the same variables raised to the same power. Add or subtract coefficients of like terms to simplify the expression.

Example: 3x+4x=7x

2y²+5−3y²+1=−y²+6

Step 3: Simplify Coefficients

If there are any coefficients that can be simplified (for example, if they are fractions), do this to make the expression cleaner.

Example:

Step 4: Arrange Terms

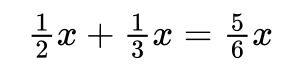
Order the terms in a standardized form, usually from highest to lowest degree of the variable (for example, in descending powers of x). This step isn’t necessary for simplification per se, but it helps in readability and is standard practice.

Example: x²+2x−x²+3→2x+3

Step 5: Factor Out Common Factors

If there’s a common factor in all terms, factor it out. This is particularly useful if the expression is part of an equation.

Example: 4x²−8x=4x(x−2)

Step 6: Simplify Any Fractions

If the expression includes fractions, simplify them by finding the greatest common divisor for the numerator and denominator or by rationalizing the denominator if needed.

Example: 4x/8x²=1/2x

Step 7: Check for Special Products

Look for opportunities to use special products or identities (like squares of binomials or difference of squares) to further simplify the expression.

Example: x²−9=(x+3)(x−3)