Logarithms

What are Logarithms?

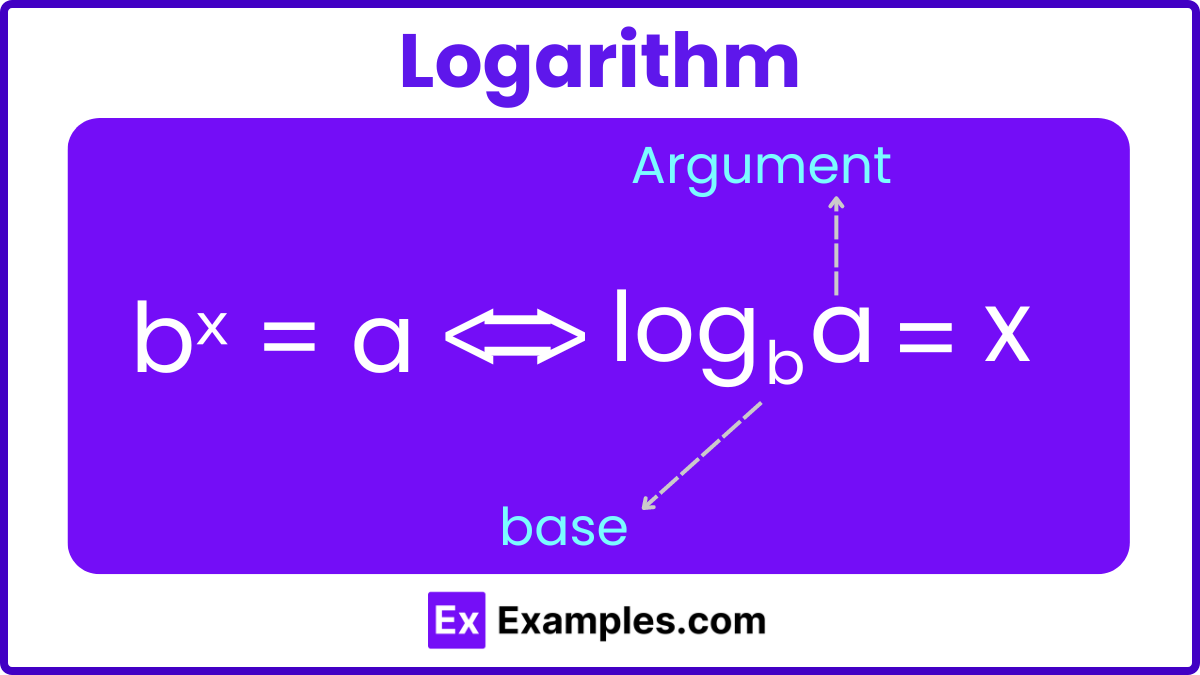
Logarithms are mathematical functions that help in solving equations involving exponents by translating multiplication of numbers into addition of their exponents. Essentially, a logarithm asks the question: “To what exponent must one number, called the base, be raised to produce another number?”

Types of Logarithms

Logarithms can be categorized based on their base, which defines the type and use of the logarithm in various mathematical contexts. Here are the three primary types of logarithms, each with its unique applications:

1. Common Logarithms (Base 10)

• Notation: log⁡ or log⁡10𝑥l
• Definition: The common logarithm of a number is the power to which the number 10 must be raised to obtain that number.
• Usage: Widely used in scientific calculations, such as measuring the intensity of earthquakes (Richter Scale) and sound (decibels).

2. Natural Logarithms (Base e)

• Notation: ln⁡𝑥
• Definition: The natural logarithm of a number is the power to which the number 𝑒e (approximately 2.71828, known as Euler’s number) must be raised to produce that number.
• Usage: Essential in calculus and solutions to problems involving growth and decay, such as population models and interest calculations.

3. Binary Logarithms (Base 2)

• Notation: log⁡2𝑥
• Definition: The binary logarithm of a number is the power to which the number 2 must be raised to reach that number.
• Usage: Fundamental in computer science, especially in algorithms and data structure operations like binary search and sorting methods.

Logarithm Rules and Properties

There are certain rules based on which logarithmic operations can be performed. The names of these rules are:

• Product rule
• Division rule
• Power rule/Exponential Rule
• Change of base rule
• Base switch rule
• Derivative of log
• Integral of log

Let us have a look at each of these properties one by one

Product Rule

In this rule, the multiplication of two logarithmic values is equal to the addition of their individual logarithms.

Log_b (mn)= log_b m + log_b n

          For example: log₃ ( 2y ) = log₃ (2) + log₃ (y)

Division Rule

The division of two logarithmic values is equal to the difference of each logarithm.

Log_b (m/n)= log_b m – log_b n

         For example, log₃ ( 2/ y ) = log_₃ (2) -log_₃ (y)

Exponential Rule

In the exponential rule, the logarithm of m with a rational exponent is equal to the exponent times its logarithm.

Log_b (mⁿ) = n log_b m

Example: log_b(2^³) = 3 log_b ²

Change of Base Rule

Log_b m = log_ₐ m/ logₐ b    

Example: log_b 2 = log_a ²/log_a b

Base Switch Rule

log_b (a) = 1 / log_a (b)

Example: log_b ⁸ = 1/log₈ b

Derivative of log

If f (x) = log_b (x), then the derivative of f(x) is given by;

f'(x) = 1/(x ln(b))

Example: Given, f (x) = log₁₀(x)

Then, f'(x) = 1/(x ln(10))

Integral of Log

∫log_b(x)dx = x( log_b(x) – 1/ln(b) ) + C

Example: ∫ log_₁₀(x) dx = x ∙ ( log₁₀(x) – 1 / ln(10) ) + C

Other Properties

Some other properties of logarithmic functions are:

• Log_b b = 1
• Log_b 1 = 0
• Log_b 0 = undefined

Logarithmic Formulas

log_b(mn) = log_b(m) + log_b(n)

logb(m/n) = log_b (m) – log_b (n)

Log_b (xy) = y log_b(x)

Log_bm√n = log_b n/m

m logb(x) + n log_b(y) = log_b(x^myⁿ)

log_b(m+n) = log_b m + log_b(1+nm)

log_b(m – n) = log_b m + log_b (1-n/m)

Difference between Log and Ln

Aspect	Log	Ln
Full Name	Logarithm	Natural Logarithm
Base	Commonly base 10	Base e (Euler’s Number, approximately 2.71828)
Notation	log⁡(𝑥) or log⁡10(𝑥)	ln⁡(𝑥)
Usage	Often used in scientific, engineering, and financial calculations involving decimal (base 10) systems.	Predominantly used in mathematics, physics, and engineering to simplify expressions involving growth rates and natural processes.
Mathematical Context	log⁡10(𝑥) means 10𝑦=𝑥	ln⁡(𝑥) means 𝑒𝑦=𝑥
Key Properties	log⁡(10)=1	ln⁡(𝑒)=1
Application Examples	Decibel levels in sound, pH levels in chemistry, and logarithmic scales used in statistics.	Natural growth and decay processes, calculating time constants in physics, and solving differential equations.
Computational Use	Common in general logarithmic calculations without specified base, often assumed base 10.	Essential in exponential growth calculations and when dealing with continuous compound interest.

Exponential Form and Logarithmic Form

Exponential Form	Logarithmic Form
𝑎𝑏=𝑐	logₐ⁡⁡𝑐=𝑏
10³=1000	log⁡₁₀1000=3
𝑒𝑥=𝑦	ln⁡𝑦=𝑥
2⁡⁴=16	log⁡₂16=4
5²=25	log⁡₅ 25=2
3−³=1/27	log⁡₃1/27=−3
𝑒⁡−¹=1𝑒	ln⁡1/𝑒=−1
1000.5=10	log⁡₁₀₀ 10=0.5

Natural Log and Common Log

Logarithms are fundamental components in mathematics, particularly useful for solving equations involving exponential functions. Among the various types of logarithms, two stand out for their frequent application and inherent properties: the natural logarithm and the common logarithm.

• Natural Logarithm (logₑ): This logarithm is also known as the natural log and is denoted by ln. It uses the base 𝑒, where e is an irrational constant approximately equal to 2.71828. The natural log is crucial in fields such as calculus, physics, and engineering due to its natural occurrence in growth processes and continuous compounding.

• Examples:
• eˣ = 3 ⇒ logₑ 3 = x (or) ln 3 = x.
• eˣ = 9 ⇒ logₑ 9 = x (or) ln 9 = x.

Common Logarithm (log₁₀): Known as the common log, this logarithm uses base 10. It is represented simply as log without any subscript. The common log is particularly useful in computations dealing with scientific notation, as it helps in managing the scale of large numbers, often seen in chemistry and astronomy.

Examples:

• 10² = 100 ⇒ log₁₀ 100 = 2 (or) log 100 = 2
• 10⁻² = 0.01 ⇒ log_₁₀ 0.01 = -2 (or) log 0.01 = -2

FAQs

Are Logarithms Algebra or Geometry?

Logarithms are primarily algebraic tools used to solve equations involving exponents. They relate to algebraic manipulation of numbers and variables.

What is a Logarithm in Simple Words?

A logarithm is a mathematical operation that determines how many times one number, called the base, must be multiplied by itself to obtain another number.

What is a Logarithm for Dummies?

A logarithm helps find the power to which a base number is raised to achieve a certain value. It simplifies dealing with exponential growth or decay.

Why Are Logarithms So Hard?

Logarithms can be challenging due to their abstract nature and the inverse operations they perform, which differ from more intuitive arithmetic operations.

What Grade Level is Log in Math?

Logarithms are typically introduced in high school, around 9th or 10th grade, often in Algebra II or Pre-Calculus classes.

Is Logarithm Part of Calculus?

Yes, logarithms are an integral part of calculus. They are crucial for solving differential equations, integration involving exponential functions, and understanding growth and decay models.