Curies Law

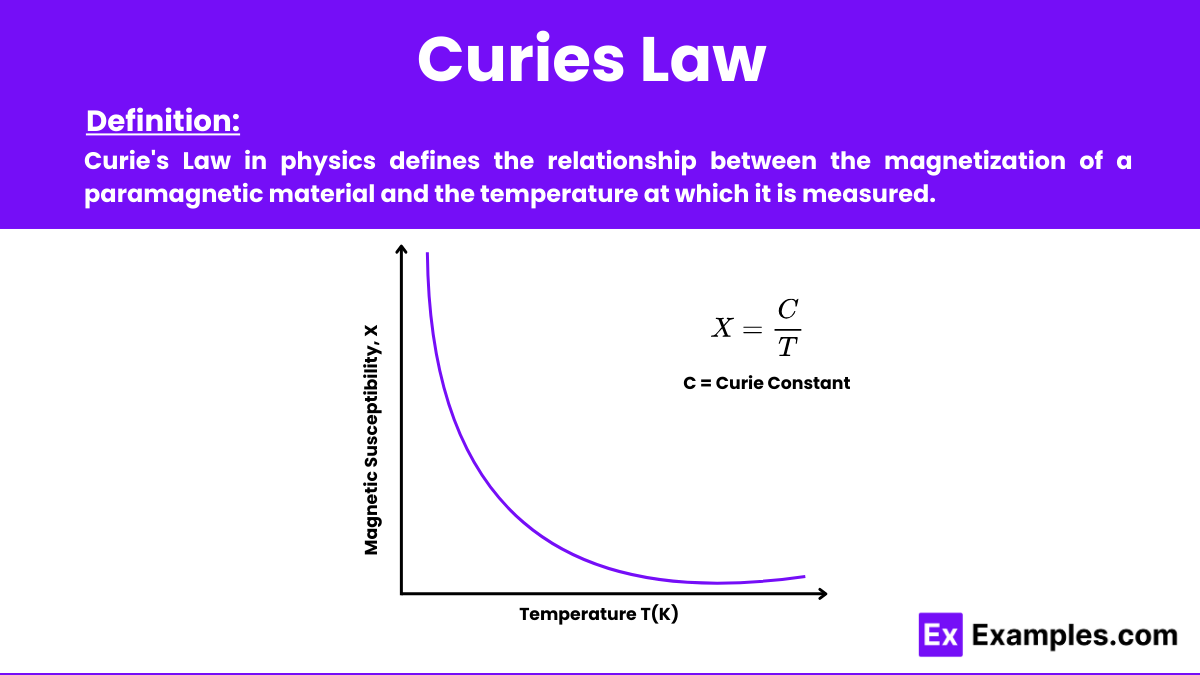
Curie’s Law in physics defines the relationship between the magnetization of a paramagnetic material and the temperature at which it is measured. This law, named after the renowned physicist Pierre Curie, states that the magnetization of a paramagnetic material is directly proportional to an applied magnetic field and inversely proportional to its temperature. In simpler terms, as the temperature increases, the ability of a paramagnetic material to magnetize decreases, provided that the magnetic field strength remains constant.

What is Curies Law?

Curie’s Law is a fundamental principle in physics that establishes how the magnetization of a paramagnetic material is influenced by temperature and the magnetic field applied to it. This law states that the magnetization of a paramagnetic material is directly proportional to the magnetic field applied and inversely proportional to its temperature.

What Is Meant By Paramagnetic?

Paramagnetic refers to the property of certain materials that are weakly attracted by an external magnetic field. This behavior occurs because of the presence of unpaired electrons in the atomic or molecular structure of the material. When exposed to a magnetic field, these unpaired electrons align their spins in the direction of the field, creating a weak attraction.

What Is The Curie Temperature?

The Curie temperature (or Curie point) is the specific temperature at which a ferromagnetic material transitions to a paramagnetic state. When you heat a ferromagnetic material above its Curie temperature, its inherent magnetic properties diminish, and it no longer maintains a permanent magnetization. This phenomenon occurs because the thermal energy disrupts the alignment of the magnetic dipoles within the material, causing them to lose their ordered arrangement and become randomly oriented.

Curies Law Formula

Curie’s Law helps describe the magnetic susceptibility of paramagnetic materials. It states that the magnetic susceptibility (𝜒χ) of a paramagnetic material is inversely proportional to its absolute temperature (T). The law is mathematically expressed as:

X = C/T​

• 𝜒 is the magnetic susceptibility of the material, which indicates how much it will become magnetized in an external magnetic field.
• 𝐶 is Curie’s constant, which is specific to the material.
• 𝑇 is the absolute temperature in Kelvin.

Curies Law Derivation

1.Magnetic Moment in an External Magnetic Field

Each atom or ion in a paramagnetic material possesses a magnetic moment (𝜇μ). In an external magnetic field, the magnetic moment tends to align with the field. The potential energy of a magnetic moment in a magnetic field is:

𝑈=−𝜇⋅𝐵

• 𝑈 is the potential energy of the magnetic moment in the external magnetic field.
• 𝜇 is the magnetic moment of a particle.
• B is the external magnetic field.

2. Thermal Energy and Alignment

The probability of finding a magnetic moment at a given energy level follows the Boltzmann distribution:

𝑃(𝐸)∝𝑒⁻ᴱ/ᴷᵀ

where:

• 𝑃(𝐸) is the probability of finding the magnetic moment in a particular energy state.
• 𝐸 is the energy of the state.
• 𝑘 is the Boltzmann constant.
• 𝑇 is the absolute temperature in Kelvin.

In this case, 𝐸=𝑈=−𝜇𝐵.

3. Net Magnetic Moment

The net magnetization 𝑀 is the sum of all magnetic moments, which depends on the balance between the magnetic alignment due to the external field and the thermal agitation that causes randomization.

4. Average Magnetic Moment

The average magnetic moment per atom due to thermal agitation is proportional to 𝜇𝐵/𝑘𝑇​ for weak magnetic fields, leading to:

⟨𝜇⟩=𝜇₀𝜇𝐵/𝑘𝑇​

5. Magnetization and Susceptibility

The magnetization 𝑀M is the total magnetic moment per unit volume:

𝑀=𝑛⟨𝜇⟩=𝑛𝜇₀𝜇𝐵/𝑘𝑇​

• 𝑛 is the number of magnetic moments per unit volume.

The magnetic sensitivity 𝜒 is defined as:

𝜒=𝑀/𝐵=𝑛𝜇₀𝜇/𝑘𝑇​

6. Curie’s Law

Curie’s Law relates the sensitivity to the absolute temperature:

X =​ C/T

• 𝐶=𝑛𝜇₀𝜇²/𝑘 is Curie’s constant.

This equation shows that magnetic sensitivity is inversely proportional to the temperature, which is the essence of Curie’s Law.

Uses of Curies Law

• Material Characterization: Curie’s Law helps scientists study materials by measuring their magnetic sensitivity at different temperatures. This reveals the type of magnetic material and its behavior at various temperature ranges.
• Magnetic Field Measurement: Using Curie’s Law, you can estimate the strength of a magnetic field. For example, knowing the sensitivity and temperature of a paramagnetic substance helps you determine the intensity of the external magnetic field.
• Magnet Design: Curie’s Law helps design paramagnetic materials in electromagnets. It allows engineers to predict how a material’s magnetic properties change with temperature.
• Research in Solid-State Physics: In solid-state physics, researchers use Curie’s Law to study how magnetic moments interact in paramagnetic materials.
• Temperature Sensors: Curie’s Law helps create temperature sensors that use magnetic sensitivity. These sensors use the predictable relationship between temperature and magnetic sensitivity for accurate temperature readings.
• Magnetic Refrigeration: Curie’s Law also helps design magnetic refrigeration systems by showing how temperature changes affect magnetic sensitivity.

Examples for Curies Law

• Paramagnetic Salts: For salts like copper sulfate, Curie’s Law helps predict magnetic sensitivity changes. As temperature rises, the magnetic sensitivity decreases, aligning well with Curie’s Law, which shows an inverse relationship between temperature and sensitivity.
• Aluminum Susceptibility: Aluminum showcases Curie’s Law in action. When exposed to a magnetic field, its sensitivity decreases with increasing temperature. This demonstrates Curie’s Law’s explanation of how magnetic sensitivity drops as temperature rises.
• Iron Above Its Curie Temperature: Once heated past its Curie temperature of 770°C, iron changes from ferromagnetic to paramagnetic. Curie’s Law helps explain the drastic drop in iron’s sensitivity at this temperature, impacting its magnetic properties.
• Magnetite and Its Magnetic Properties: Magnetite has strong magnetic properties, but only below its Curie temperature. Curie’s Law shows how magnetite’s magnetic sensitivity declines as it approaches this temperature, turning it paramagnetic.
• Lanthanum Manganite in Research: Compounds like lanthanum manganite are key in advanced research, where Curie’s Law is significant.

FAQ’S

What is the inverse Curie law?

This Curie’s Law involves the inverse proportionality of magnetic sensitive to temperature minus the Curie-Weiss constant, commonly used in paramagnetic behavior.

What is the Curie’s principle?

It states that the symmetry elements present in the causes of a physical phenomenon are also found in the phenomenon itself.

Who invented Curie law?

Pierre Curie, introduced Curie’s Law, fundamentally advanced magnetic material research.