Gravitational Acceleration Formula – Formula,

What is Gravitational Acceleration Formula?

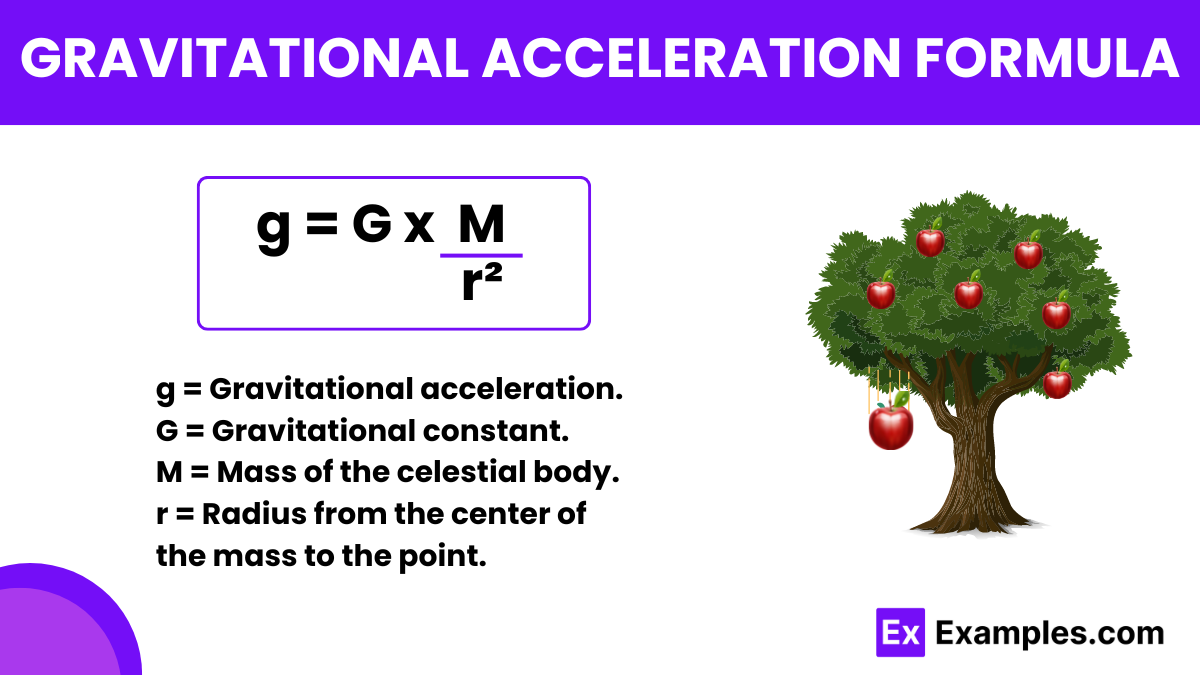
Gravitational acceleration refers to the acceleration of an object caused by the force of gravity from another object, typically a planet or a moon. The most common formula to calculate gravitational acceleration is derived from Newton’s Law of Universal Gravitation, discovered by Sir Isaac Newton in the late 17th century. Newton’s groundbreaking work established the foundational principles that describe how objects attract each other with a force proportional to their masses and inversely proportional to the square of the distance between their centers.

We express the standard formula for gravitational acceleration as:

• g is the gravitational acceleration.
• G is the gravitational constant (6.67430 ×10⁻¹¹ m³ kg⁻¹ s⁻²).
• M is the mass of the celestial body (like Earth).
• r is the radius from the center of the mass to the point where the acceleration is being measured.

For objects not at the Earth’s surface but at a height h above it, the formula adjusts to account for the increased distance from the Earth’s center. This variation is important for calculations involving satellites or high-altitude flights. The modified formula becomes:

• R is the Earth’s radius.

As h increases, g decreases, illustrating the inverse square law inherent in gravitational interactions.

Another essential formula relates to objects in free fall near the Earth’s surface, where gravitational acceleration is approximated as a constant:

This value simplifies many physics calculations involving motion near the Earth’s surface and assumes a uniform gravitational field without significant variation in altitude or geographical location. These formulas allow physicists and engineers to calculate how quickly objects will accelerate towards each other or the ground, providing crucial data for everything from engineering to aerospace development.

Derivation of Gravitational Acceleration Formula

Step 1: Define Newton’s Law of Universal Gravitation

Newton’s Law of Universal Gravitation states that two masses (M and m) separated by a distance (r) exert a force (F) on each other as given by: F = G x ( M × m) / r²

• F is the gravitational force,
• G is the gravitational constant (approximately 6.674×10⁻¹¹ m³ kg⁻¹ s⁻² ),
• M is the mass of the larger object (e.g., Earth),
• m is the mass of the smaller object,
• 𝑟 is the distance between the centers of the two masses.

Step 2: Apply Newton’s Second Law of Motion

Newton’s second law states that force equals mass times acceleration (𝐹 = 𝑚a). In the context of gravitational force, the acceleration due to gravity (g) on the smaller mass m can be expressed as:

Step 3: Equate and Solve for g

Setting the two expressions for force equal to each other gives:

To find the gravitational acceleration g, divide both sides by m (assuming 𝑚≠0):

It states that the Gravitational acceleration (g) at a distance 𝑟 from the center of mass 𝑀 is directly proportional to 𝑀 and inversely proportional to the square of 𝑟.

Usages of the Gravitational Acceleration Formula

• Space Exploration: It helps calculate satellite orbits and plan spacecraft trajectories.
• Aerospace Engineering: Engineers use it to design flight paths and simulate space conditions.
• Geophysics: The formula aids in estimating Earth’s mass distribution, essential for understanding internal structures.
• Oceanography: It impacts modeling of tides and ocean currents.
• Civil Engineering: Knowing gravitational acceleration is vital for building structures like skyscrapers and bridges.

Limitations of the Gravitational Acceleration Formula

• Point Mass Assumption: It simplifies objects to point masses, which isn’t always accurate for large or close bodies.
• Uniform Sphere Assumption: It assumes celestial bodies are perfectly spherical with uniform density.
• Excludes External Forces: The formula doesn’t consider forces like electromagnetic influences or Atmospheric drag.
• Non-relativistic: General Relativity becomes necessary near black holes or at high velocities where the standard formulas are not suitable.
• Ignores Variations: It overlooks changes in gravitational pull due to altitude, Latitude, or Earth’s rotation.

FAQs

What is an Example of Gravitational Acceleration?

An example of gravitational acceleration is an apple falling from a tree due to Earth’s gravity, accelerating at approximately 9.81 m/s².

What Does the Gravitational Acceleration Formula Calculate?

The formula calculates the acceleration due to gravity exerted by a mass (like a planet) on objects at a specific distance from its center.

How is Gravitational Acceleration Measured Near Earth?

Devices called Gravimeters measure gravitational acceleration near Earth by detecting changes in Gravitational pull.