What is the formula for gravitational force between two masses?
F = Gm₁m₂/r²
F = Gm₁m₂r²
F = Gm₁m₂r
F = Gm₁m₂/r
of 10
Gravity Formula – Formula, Applications, Example Problems
Gravity Formula – Formula, Applications, Example Problems
What is Gravity Formula?
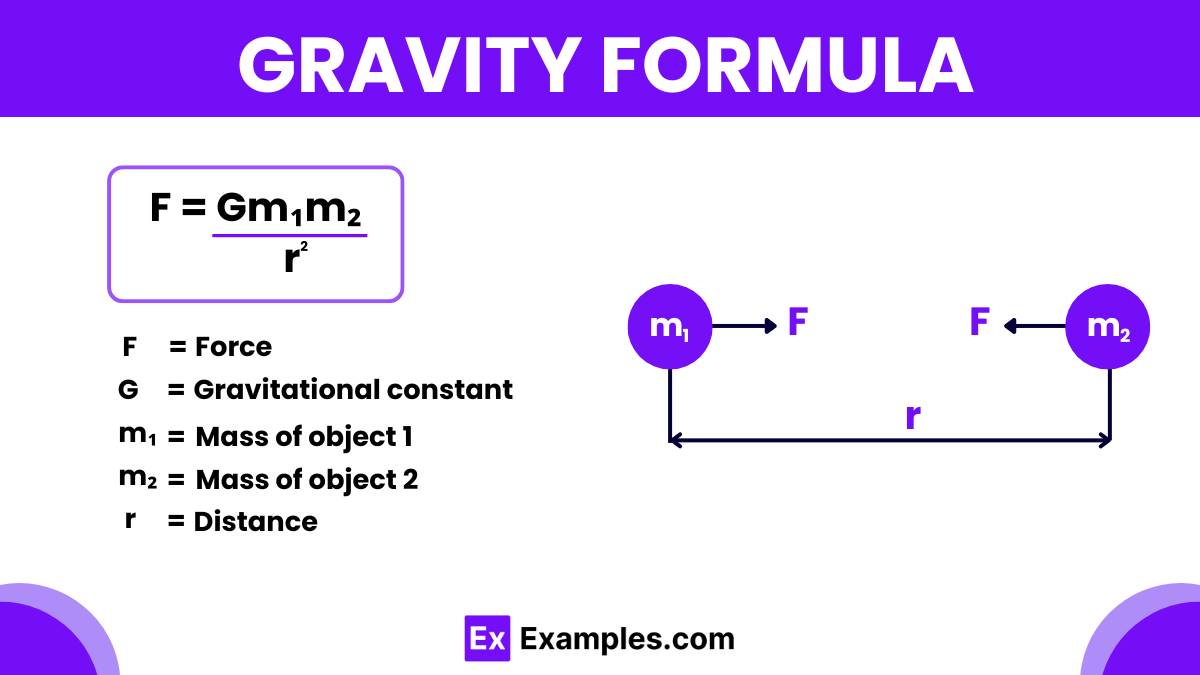
The gravity formula, often referred to as the formula for gravitational force, is a key concept in physics that describes the force of attraction between two objects due to their masses. Discovered by Sir Isaac Newton in the 17th century, this formula is fundamental to understanding how objects interact in space. Newton’s law of universal gravitation states that every particle of matter in the universe attracts every other particle with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers.The formula for gravitational force is expressed as
- 𝐹 represents the gravitational force between two masses.
- 𝐺 is the gravitational constant.
- m₁ and m₂ are the masses of the objects.
- 𝑟 is the distance between the centers of the two masses.
This formula not only plays a crucial role in physics for calculating the forces acting between bodies but also helps predict the movements of planets and stars in the cosmos. By applying this formula, scientists can understand and predict the gravitational interactions in various systems, from the orbits of planets to the paths of comets and the behavior of galaxies.
Applications of Gravity Formula
- Space Exploration: Scientists use the gravity formula to calculate the trajectories of spacecraft, ensuring they navigate correctly between planets.
- Orbital Predictions: It helps in predicting the orbits of satellites around the Earth, crucial for GPS systems and telecommunications.
- Astronomy: The formula assists astronomers in studying the orbits of planets and stars, enhancing our understanding of the universe.
- Engineering: Engineers apply the gravity formula in designing structures like bridges and skyscrapers to withstand gravitational forces.
- Climate Science: Researchers use it to understand sea level changes and movements of tectonic plates affecting Earth’s gravity field.
Example Problems on Gravity Formula
Problem 1: Calculating Gravitational Force Between Earth and Moon
Question: Calculate the gravitational force between the Earth and the Moon. Assume the mass of the Earth (𝑚₁) is approximately 5.97×10²⁴ kg, the mass of the Moon (𝑚₂) is about 7.35×10²² kg, and the distance between them (𝑟) is 3.84×10⁸ meters.
Solution:
Apply the Gravity Formula: F = G x ( (m₁ x m₂) / r²) where G (gravitational constant) = 6.674×10⁻¹¹ N(m/kg)².
Substitute the values:𝐹= ( 6.674 × 10⁻¹¹ ) x ( (( 5.97 × 10²⁴ ) x (7.35 × 10²² ) ) / (3.84 × 10⁸ )² )
Calculate the force: The gravitational force 𝐹 equals approximately 1.98×1020 Newtons.
Problem 2: Gravitational Attraction Between Two Students
Question: Two students, each with a mass of 50 kg, are sitting 2 meters apart in a classroom. Calculate the gravitational force between them.
Solution:
Use the Gravity Formula:F = G x ( (m₁ x m₂) / r²)
Substitute the values:𝐹 = ( 6.674 × 10⁻¹¹ ) x ( (50) x (50)) / (2)²
Calculate the force: The gravitational force F equals approximately 4.17×10⁻⁹ Newtons.
Problem 3: Force Between a Planet and a Sun
Question: A planet with a mass of 4.8×10²⁴ is orbiting a sun whose mass is 1.99×10³⁰ kg. The distance between the planet and the sun is 1.5×10¹¹ meters. Find the gravitational force exerted between them.
Solution:
Apply the Gravity Formula: F = G x (m₁ x m₂) / r²
Insert the given values:
𝐹 = (6.674 × 10⁻¹¹) x ( (4.8 × 10²⁴) x (1.99 × 1030) ) / (1.5×1011)²)
Perform the calculation: The gravitational force 𝐹 is approximately 3.56×10²² Newtons.
FAQs
How is 9.8 m/s² Calculated for Gravity?
The 9.8 m/s² value is derived from measuring the acceleration of objects in free fall near the Earth’s surface, standardized globally.
How Do You Calculate Gravity g?
Gravity 𝑔 is calculated by observing the acceleration of an object in free fall, with Earth’s average gravitational acceleration being approximately 9.8 m/s².
What is 9.8 m/s²?
9.8 m/s² is the average acceleration due to Earth’s gravitational pull on objects near its surface, used as a standard in physics calculations.
Share :
Practice Test
What does G represent in the gravitational force formula?
Gravitational mass
Gravitational acceleration
Gravitational constant
Gravitational force
of 10
If the distance between two masses is doubled, what happens to the gravitational force between them?
It remains the same
It is halved
It is quartered
It doubles
of 10
What is the value of the gravitational constant (G)?
6.674 x 10⁻¹¹ N(m/kg)²
9.81 m/s²
3 x 10⁸ m/s
6.674 x 10⁻¹⁰ N(m/kg)²
of 10
What happens to the gravitational force if the mass of one object is tripled while the other mass and distance remain constant?
It remains the same
It is halved
It is tripled
It is quartered
of 10
How does the gravitational force between two objects change if both masses are doubled?
It remains the same
It is quadrupled
It is doubled
It is halved
of 10
In the formula F = Gm₁m₂/r², what does r represent?
Radius of one mass
Distance between the centers of the two masses
Radius of both masses
Gravitational constant
of 10
What unit is used to measure gravitational force?
Newton
Joule
Pascal
Watt
of 10
If the distance between two objects is reduced to one-third, how does the gravitational force change?
It remains the same
It increases by a factor of 3
It increases by a factor of 9
It decreases by a factor of 3
of 10
What does the gravitational force between two objects depend on?
Their masses and the distance between them
Their volumes and the distance between them
Their masses and their velocities
Their velocities and the distance between them
of 10