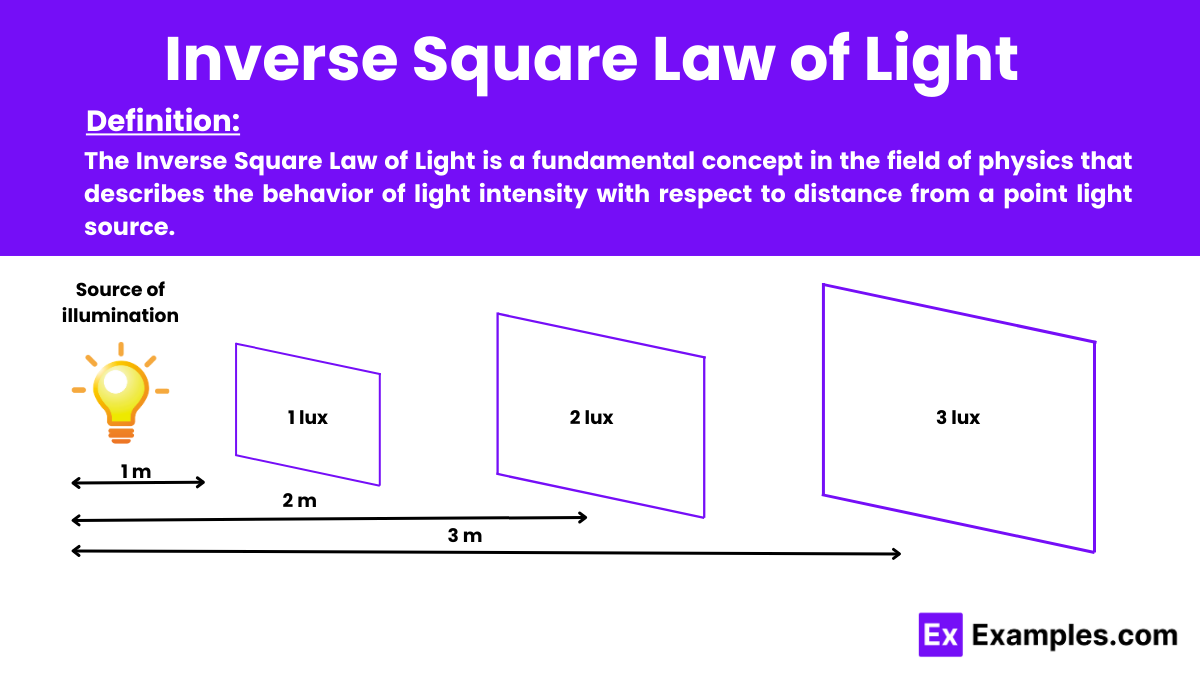
What is the inverse square law of light?
Light intensity is inversely proportional to the square of the distance from the source
Light intensity is directly proportional to the square of the distance from the source
Light intensity is inversely proportional to the distance from the source
Light intensity is directly proportional to the distance from the source