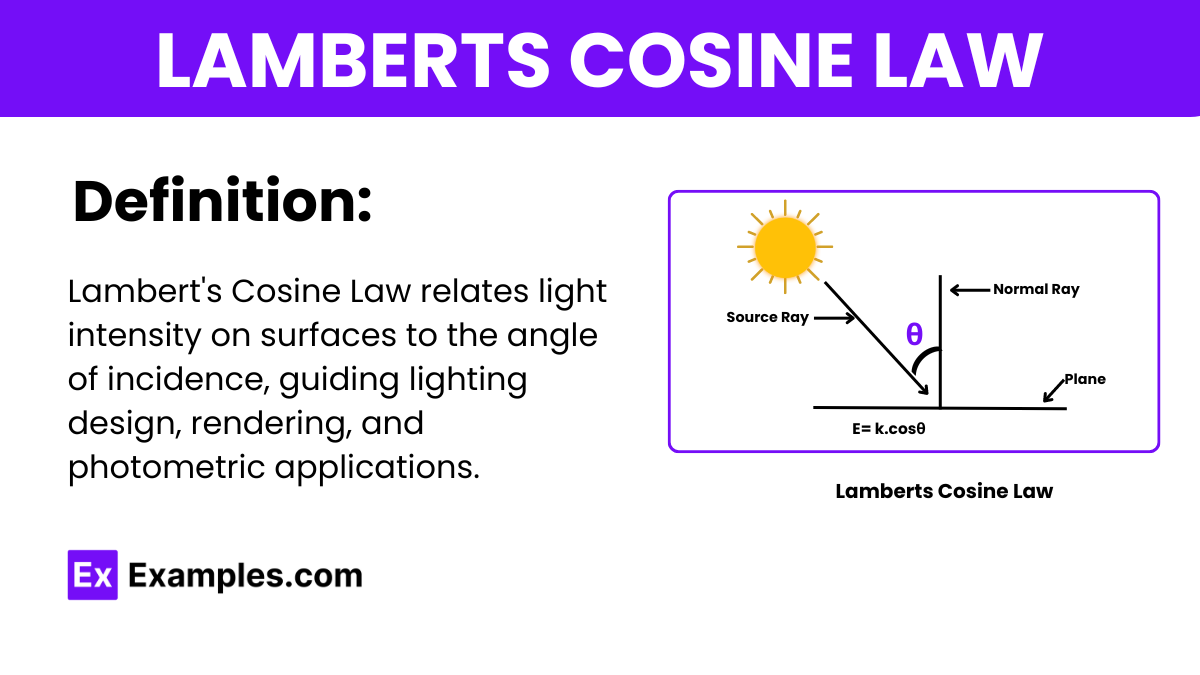
What does Lambert\'s Cosine Law describe?
The relationship between current and voltage in a resistor
The intensity of light on a surface as a function of angle
The force between two charged particles
The energy of a photon as a function of its wavelength