What is the formula for the Lorentz force experienced by a charged particle in a magnetic field?
F = qE + q(v × B)
F = qE - q(v × B)
F = q(E + v × B)
F = q(E - v × B)
of 10
Lorentz Force Law – Formulas, Applications, FAQs, usage
Lorentz force Law
Equation of Lorentz force Law
Where:
- 𝐹 is the total force exerted on the particle,
- 𝑞 is the electric charge of the particle,
- 𝐸 is the electric field,
- 𝑣 is the velocity of the particle,
- 𝐵 is the magnetic field,
- × denotes the cross product, which indicates that the force direction is perpendicular to both the velocity of the particle and the magnetic field.
Key Components of the Lorentz Force
- Electric Force: 𝑞𝐸 – This component states that a charged particle in an electric field will experience a force that is proportional to the charge and the strength of the electric field. The direction of the force depends on the direction of the electric field and the sign of the charge.
- Magnetic Force: 𝑞𝑣×𝐵 – This part of the Lorentz force arises only when the charged particle is moving relative to the magnetic field. The magnitude of the force depends on the charge, the speed of the particle, the strength of the magnetic field, and the angle between the velocity and the magnetic field vectors. Crucially, the direction of this force is perpendicular to both the velocity of the particle and the magnetic field.
Usage of the Lorentz Force Law
- Mass Spectrometry: The Lorentz force is utilized in mass spectrometers to separate ions based on their mass-to-charge ratios. By analyzing the trajectories of ions in magnetic and electric fields, the device can determine the properties of the substances.
- Cyclotrons and Synchrotrons: These particle accelerators use magnetic fields to bend the paths of charged particles, effectively increasing their energy through repeated cycling within the magnetic field, guided by the Lorentz force.
- Hall Effect Sensors: These devices measure the magnitude of a magnetic field via the Lorentz force. When a current-carrying conductor is placed in a magnetic field, the Lorentz force moves the charge carriers, creating a voltage (Hall voltage) that can be measured.
- Magnetic Levitation: Maglev trains use magnetic fields to lift, propel, and guide a vehicle over a track. The Lorentz force plays a critical role in balancing the gravitational pull, essentially allowing for frictionless movement.
- Electric Motors and Generators: In these devices, the Lorentz force is responsible for converting electrical energy to mechanical energy and vice versa. The interaction between electric currents and magnetic fields within the motor or generator creates forces that turn the rotor.
Equations with SI units convention
The SI unit of the Lorentz force is the newton (N). The Lorentz force law describes the force experienced by a charged particle moving through electric and magnetic fields.
Equations with cgs units convention
In the cgs (centimeter-gram-second) system, the Lorentz force is measured in dynes. The formula for the Lorentz force remains the same, but the units change: charge in statcoulombs, electric field in statvolts per centimeter, velocity in centimeters per second, and magnetic field in gauss. This results in force expressed in dynes.
Lorentz Force Law: Table Format
| Variable | Symbol | Unit | Role in Lorentz Force |
|---|---|---|---|
| Electric Field | 𝐸 | Volts per meter (V/m) | Generates force on charge regardless of its motion |
| Magnetic Field | 𝐵 | Tesla (T) or Weber per square meter (Wb/m²) | Influences moving charges, perpendicular to motion |
| Charge | 𝑞 | Coulomb (C) | Determines magnitude of the force; sign affects direction |
| Velocity of Charge | 𝑣 | Meters per second (m/s) | Speed and direction of charge; crucial for magnetic force |
| Lorentz Force | 𝐹 | Newton (N) | Resultant force acting on the charge |
Significance of the Lorentz force easy way
Movement and Direction of Charged Particles
The Lorentz force dictates the path that charged particles, like electrons and protons, take when they move through electric and magnetic fields. The direction and speed of their movement are influenced by the characteristics of these fields and the particles’ own properties (such as charge and velocity).
Technology and Devices
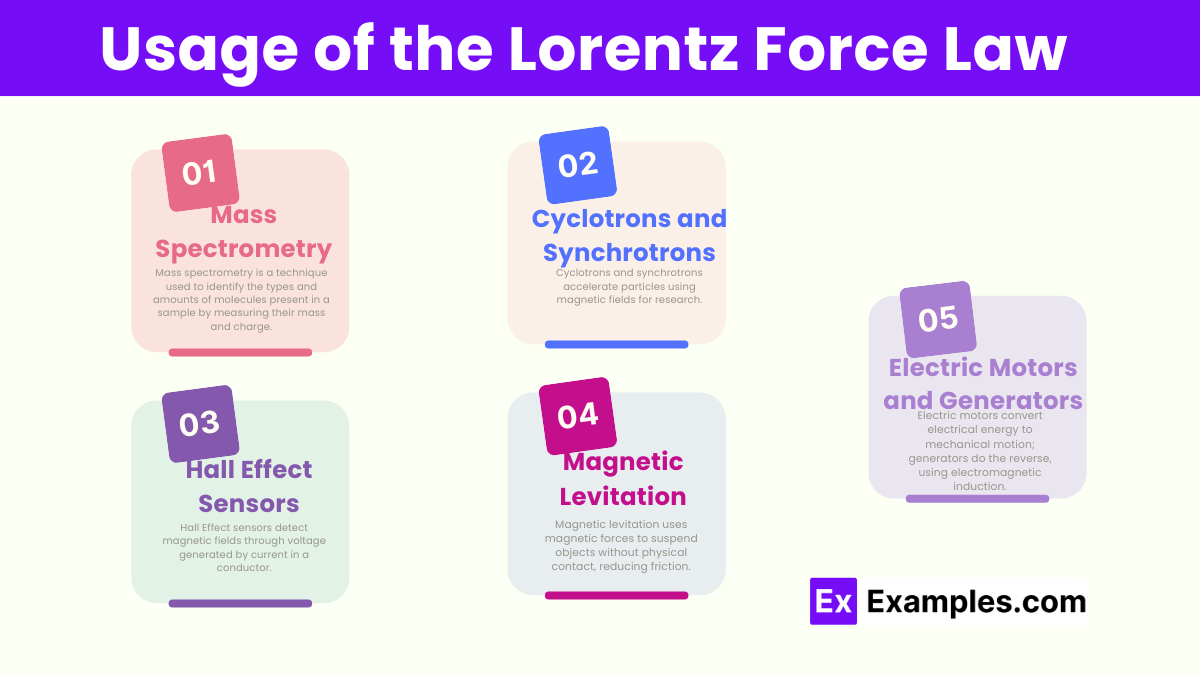
This force is essential in the operation of various technological devices and systems:
- Electric Motors and Generators: These devices convert electrical energy into mechanical motion (and vice versa) thanks to the Lorentz force acting on moving charges within a magnetic field.
- Particle Accelerators: Devices like cyclotrons use the Lorentz force to accelerate charged particles to high speeds, essential for research in nuclear and particle physics.
- Mass Spectrometers: These instruments separate particles with different mass-to-charge ratios by manipulating their paths with electric and magnetic fields, relying on the Lorentz force for precise measurements.
Understanding Fundamental Physics
The Lorentz force is crucial for experiments and theories in electromagnetism, one of the four fundamental forces of nature. It helps scientists understand how charged particles interact, leading to deeper insights into the structure of matter and the fundamental forces that govern the universe.
Everyday Applications
- Magnetic Levitation (Maglev) Trains: These trains levitate above their tracks without contact, reducing friction dramatically. The Lorentz force is used to lift, stabilize, and propel these trains, allowing for faster and smoother rides.
Navigation and Sensing
- Hall Effect Sensors: These sensors use the Lorentz force to detect magnetic fields and are widely used in automotive and industrial applications for position sensing, timing, and switching.
FAQs
Does the Lorentz force act on neutral particles?
No, the Lorentz force only acts on particles with an electric charge. Neutral particles do not experience this force directly, although they can still be affected indirectly if they are part of a neutral system that contains charged particles.
How does the Lorentz force affect the motion of a charged particle?
The Lorentz force affects the motion of a charged particle by changing its direction and/or speed. In an electric field, the force is along the direction of the field for positive charges and opposite for negative charges. In a magnetic field, the force is perpendicular to both the velocity of the particle and the magnetic field, causing the particle to move in a circular or spiral path.
Can the Lorentz force be used to generate electricity?
Yes, the Lorentz force is fundamental in generators, where the motion of a conductor through a magnetic field induces an electromotive force (voltage) across the conductor by the Lorentz force, generating electricity.
Is the Lorentz force conservative?
No, the magnetic component of the Lorentz force is non-conservative. This means that the work done by the magnetic part of the Lorentz force on a charged particle moving around a closed path is zero, and it does not depend on the path taken by the particle.
Share :
Practice Test
Which component of the Lorentz force is due to the electric field?
qE
q(v × B)
q(E × B)
q(v × E)
of 10
Which component of the Lorentz force is due to the magnetic field?
qE
q(v × B)
q(E × B)
q(v × E)
of 10
If a charged particle is moving parallel to the magnetic field, what is the magnetic force acting on it?
Zero
qvB
qE
q(E + vB)
of 10
What direction does the magnetic force on a charged particle moving in a magnetic field act?
Parallel to the velocity
Perpendicular to both the velocity and magnetic field
Parallel to the magnetic field
Opposite to the velocity
of 10
What happens to the magnitude of the Lorentz force if the charge of the particle is doubled?
It remains the same
It is halved
It doubles
It becomes zero
of 10
How does the direction of the electric force on a positive charge relate to the direction of the electric field?
Opposite
Same
Perpendicular
No relation
of 10
What is the effect of reversing the direction of the magnetic field on the magnetic component of the Lorentz force?
No effect
It doubles
It reverses direction
It halves
of 10
If a charged particle is at rest in an electric field, what is the Lorentz force acting on it?
Zero
qE
q(v × B)
q(E + v × B)
of 10
In which situation will a charged particle experience the greatest magnetic force?
Moving parallel to the magnetic field
Moving perpendicular to the magnetic field
At rest in the magnetic field
Moving at an angle of 45 degrees to the magnetic field
of 10