Resultant Force Formula – Formula, Applications, Example Problems

What is Resultant Force Formula?

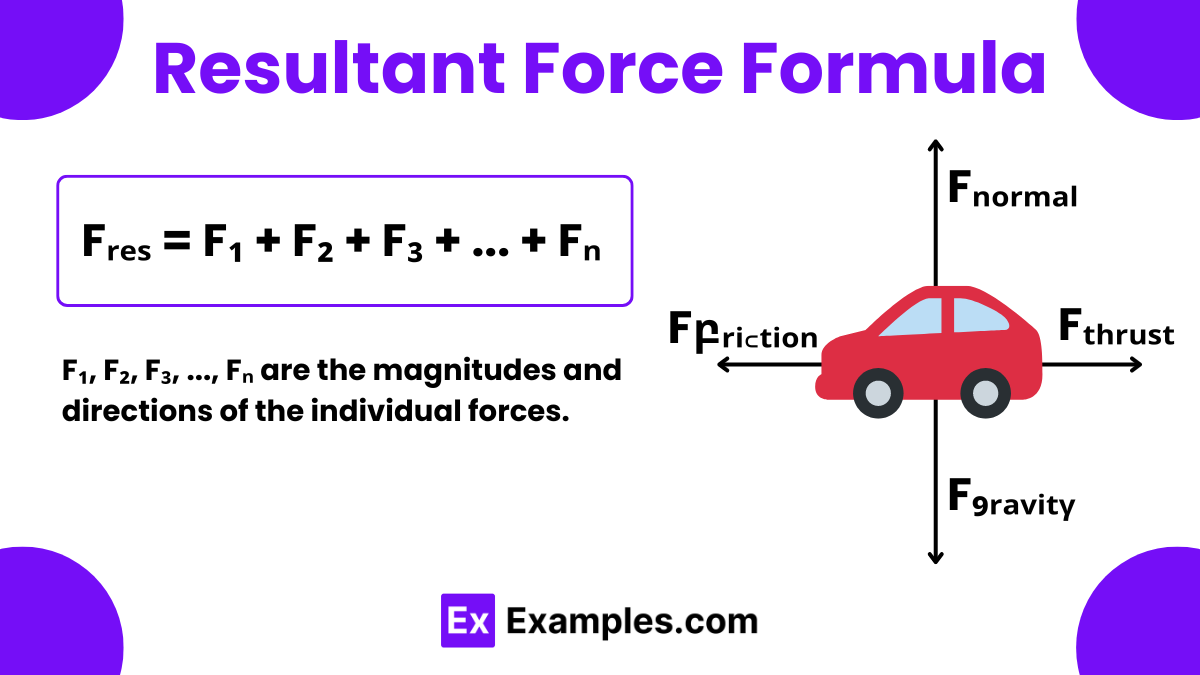
The Resultant Force Formula is a crucial equation in physics that allows us to calculate the single force acting on an object when multiple forces are at play. This formula is fundamental in the study of dynamics, which is the branch of physics concerned with the motion of objects influenced by forces. The formula states that the resultant force (Fᵣ) is the vector sum of all individual forces acting on an object. Mathematically, it can be expressed as

F₁, F₂, F₃, …, Fₙ are the magnitudes and directions of the individual forces.

The concept of the resultant force and its mathematical determination were developed as part of classical mechanics, primarily influenced by the work of Sir Isaac Newton in the 17th century. Newton’s laws of motion describe how and why objects move, and his second law, in particular, forms the basis for calculating resultant forces. It establishes the relationship between an object’s mass, its acceleration, and the applied force, leading to the development of the formula for resultant forces.

This formula is essential for solving problems where multiple forces act on a single object, allowing us to predict the object’s motion. By using the resultant force formula, physicists and engineers can determine how forces interact and influence the behavior of physical systems, from simple mechanical devices to complex structures like bridges and spacecraft. Whether calculating the tension in cables, the stability of structures, or the trajectory of moving objects, the resultant force formula is a cornerstone of physical calculations.

Applications of Resultant Force Formula

• Vehicle Dynamics: Engineers use the resultant force formula to analyze and improve vehicle stability and handling. By understanding how different forces like gravity, friction, and air resistance interact, they can design vehicles that are safer and perform better under various conditions.
• Structural Engineering: In structural engineering, the formula helps determine the force distribution within buildings and bridges. This ensures structures can withstand forces like wind, weight, and earthquakes without failing.
• Sports Physics: The resultant force formula is vital in sports science to enhance athletic performance and design better sports equipment. For example, it helps in analyzing the forces acting on a soccer ball when kicked or the impact forces absorbed by running shoes.
• Aerospace Engineering: Aerospace engineers apply the resultant force formula to calculate the necessary thrust and lift forces for aircraft and spacecraft. This ensures that vehicles achieve the desired altitude and trajectory during flight.
• Mechanical Systems: The formula is crucial for designing mechanical systems where multiple forces are involved, such as in elevators or cranes, ensuring they operate safely and efficiently under load.

Example Problems on Resultant Force Formula

Example 1: Calculating Resultant Force in a Straight Line

Problem: Two people push a stationary car. One applies a force of 200 N to the east. The other applies a force of 150 N to the east. Calculate the resultant force on the car.

Solution:

• The forces are in the same direction, so we simply add them together.
• Resultant force (Fᵣₑₛ) = 200 N + 150 N = 350 N
• The resultant force on the car is 350 N to the east.

Example 2: Resultant Force at an Angle

Problem: A boat is being pulled by two forces. One force of 100 N is directed north and another force of 100 N is directed east. Calculate the resultant force.

Solution:

• Since the forces are perpendicular, use the Pythagorean theorem to find the resultant.
• Resultant force (Fᵣₑₛ) = √(100² N² + 100² N²) = √(10,000 N² + 10,000 N²) = √20,000 N² = 141 N
• The resultant force is approximately 141 N northeast.

Example 3: Opposing Forces

Problem: A sled is being pulled from opposite sides. One person pulls with a force of 250 N east, while another pulls with a force of 180 N west. Calculate the resultant force.

Solution:

• The forces are in opposite directions, so subtract the smaller force from the larger force.
• Resultant force (Fᵣₑₛ) = 250 N (east) – 180 N (west) = 70 N
• The resultant force on the sled is 70 N to the east.

FAQs

How Do You Calculate the Resultant Force?

To calculate the resultant force, sum up all individual forces acting on an object, considering both magnitude and direction.

What is the Resultant Force of Two Vectors?

The resultant force of two vectors is the vector sum of both forces, calculated using vector addition.

What is the Formula for Resultant Moment of Force?

The formula for resultant moment of force is 𝜏=𝑟×𝐹, where 𝑟 is the position vector and 𝐹 is the force vector.

What is the Formula for Resultant Acceleration?

The formula for resultant acceleration is 𝑎 = 𝐹ₙₑₜ / 𝑚​​, where 𝐹ₙₑₜ is the net force and 𝑚 is the mass of the object.