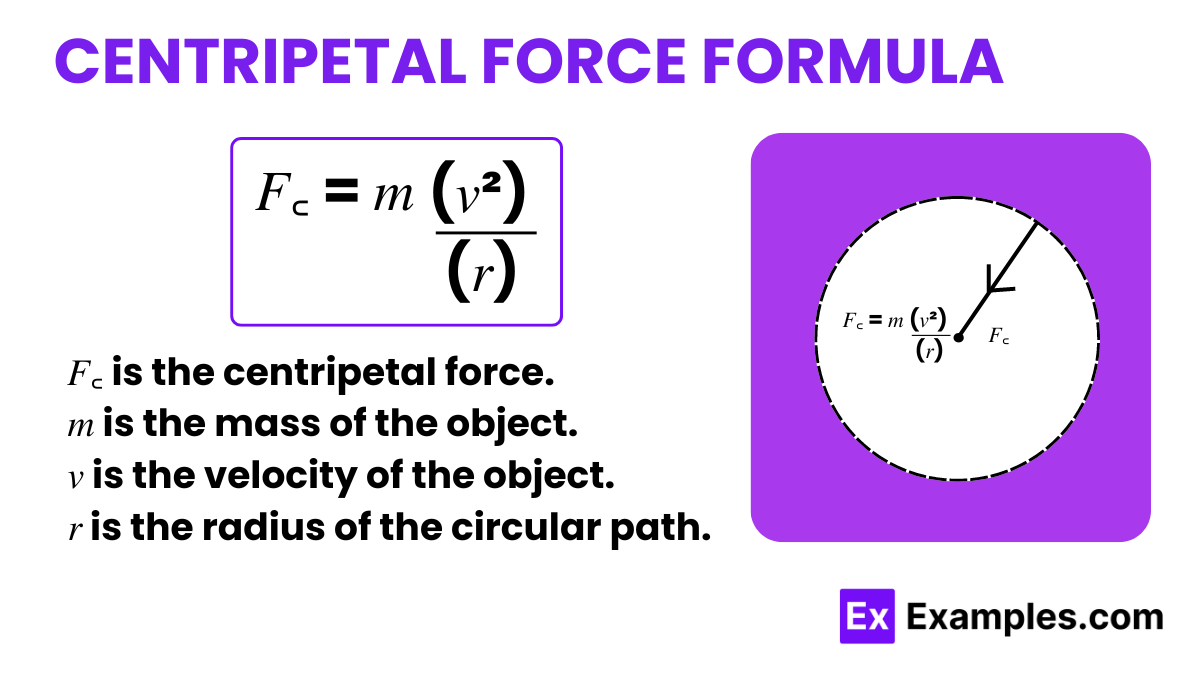
Centripetal Force Formula

What is Centripetal Force Formula?

The centripetal force formula is a key equation in physics that quantifies the force required to maintain an object’s motion along a circular path. This formula is crucial for understanding and predicting the behaviors of objects in circular motion, ranging from electrons in magnetic fields to cars turning on curved roads. It specifically calculates the necessary inward force that keeps an object moving in a circle at a constant speed, without spiraling outwards or inwards.

Sir Isaac Newton first derived this formula based on his laws of motion, particularly the second law, which relates force to mass and acceleration. In the case of circular motion, the relevant acceleration is centripetal acceleration, which always points toward the center of the circle. The centripetal force formula is mathematically expressed as

𝐹꜀ = 𝑚 x (𝑣²/𝑟)

𝐹꜀ is the centripetal force.
𝑚 is the mass of the object.
𝑣 is the velocity of the object.
𝑟 is the radius of the circular path.

This formula indicates that the centripetal force depends directly on the mass of the object and the square of its velocity, and inversely on the radius of the path. Such a relationship is pivotal for ensuring stability in systems undergoing rotational motion, allowing for precise calculations in engineering and physics applications. By applying Newton’s second law,

𝐹 = 𝑚 x a

and recognizing that the acceleration a in circular motion is given by

𝑎꜀=𝑣² / 𝑟

we derive the specific formula for the force keeping an object in circular motion. This highlights the seamless integration of Newtonian mechanics into understanding and solving practical problems in real-world physics scenarios.

Applications of Centripetal Force Formula

Amusement Park Rides: Designers use the centripetal force formula. To ensure safety and stability on rides like roller coasters and merry-go-rounds, where passengers experience circular motion.
Vehicle Dynamics: Engineers apply the formula to design safer curved roads and racetracks, calculating the necessary banking angles and speed limits to prevent vehicles from skidding outward.
Satellite Orbits: Space agencies calculate the required centripetal force to keep satellites in stable orbits around the Earth, ensuring they do not drift into space or fall back to Earth.
Athletics: In track and field, the formula helps athletes understand the force needed to spin a hammer or discus effectively in a circular path before release.
Centrifuges: Used extensively in medical and research labs, centrifuges apply centripetal force to separate substances of different densities by spinning samples at high speeds.
Planetary Motion: The formula fundamentally explains the orbits of planets and moons in astrophysics, as gravitational attraction governs their centripetal force.

Example Problems on Centripetal Force Formula

Problem 1: Calculating Centripetal Force on a Car Turning a Curve

A car with a mass of 1500 kg is traveling around a curve with a radius of 50 meters at a speed of 20 meters per second. Calculate the centripetal force exerted on the car to maintain its circular path.

Solution: Using the centripetal force formula 𝐹꜀=𝑚 x (𝑣² / 𝑟)

𝐹꜀=1500 (20² / 50) =1500 (400 / 50) = 1500×8 = 12,000 N

Thus, the centripetal force required is 12,000 Newtons.

Problem 2: Determining Speed of an Object in Circular Motion

A 5 kg object is tied to a string and swung in a horizontal circle with a radius of 2 meters. If the tension in the string providing the centripetal force is 98 Newtons, what is the speed of the object?

Solution: Rearrange the centripetal force formula to solve for velocity v: 𝐹𝑐=𝑚 x (𝑣² / 𝑟)

98=5 (𝑣² / 2)

v² / 2 =98 / 5

v² = (98 / 5) × 2 =39.2

𝑣 = √39.2 ≈ 6.26 m/s The object’s speed is approximately 6.26 meters per second.

Problem 3: Centripetal Force in a Washing Machine

During the spin cycle, a washing machine spins clothes at a rate of 800 revolutions per minute (rpm) in a drum of radius 0.3 meters. Calculate the centripetal force acting on a 0.5 kg wet shirt.

Solution: First, convert rpm to radians per second:

Angular velocity (𝜔)=800 × (2𝜋 / 60) ≈ 83.78 rad/s

The linear velocity 𝑣v is given by 𝑣=𝑟𝜔:

𝑣=0.3×83.78≈25.13 m/s

Now, use the centripetal force formula: 𝐹𝑐 = 𝑚 (𝑣² / r)

𝐹𝑐 =0.5 (25.13² / 0.3)

𝐹𝑐=0.5 × (631.53 / 0.3) ≈1052.55 N.

The centripetal force on the shirt is approximately 1052.55 Newtons.

FAQs

How is Centripetal Force Calculated?

Centripetal force is calculated using the formula 𝐹𝑐 = 𝑚 (𝑣² / r). Where m is mass, v is velocity, and r is radius.

What is the Formula for Centripetal Force and Acceleration?

The formula for centripetal force is 𝐹𝑐 = 𝑚 (𝑣² / r) . For acceleration, it is a = (𝑣² / r).

What is the Formula of Centripetal and Centrifugal Force?

Centripetal force formula: 𝐹𝑐 = 𝑚 (𝑣² / r). Centrifugal force, perceived in a rotating frame, mirrors this: 𝐹բ=𝑚 (𝑣² / r).

Centripetal Force Formula