What does Malus's Law describe?
The relationship between electric and magnetic fields
The intensity of light passing through a polarizer
The wavelength of light in different mediums
The frequency of electromagnetic waves

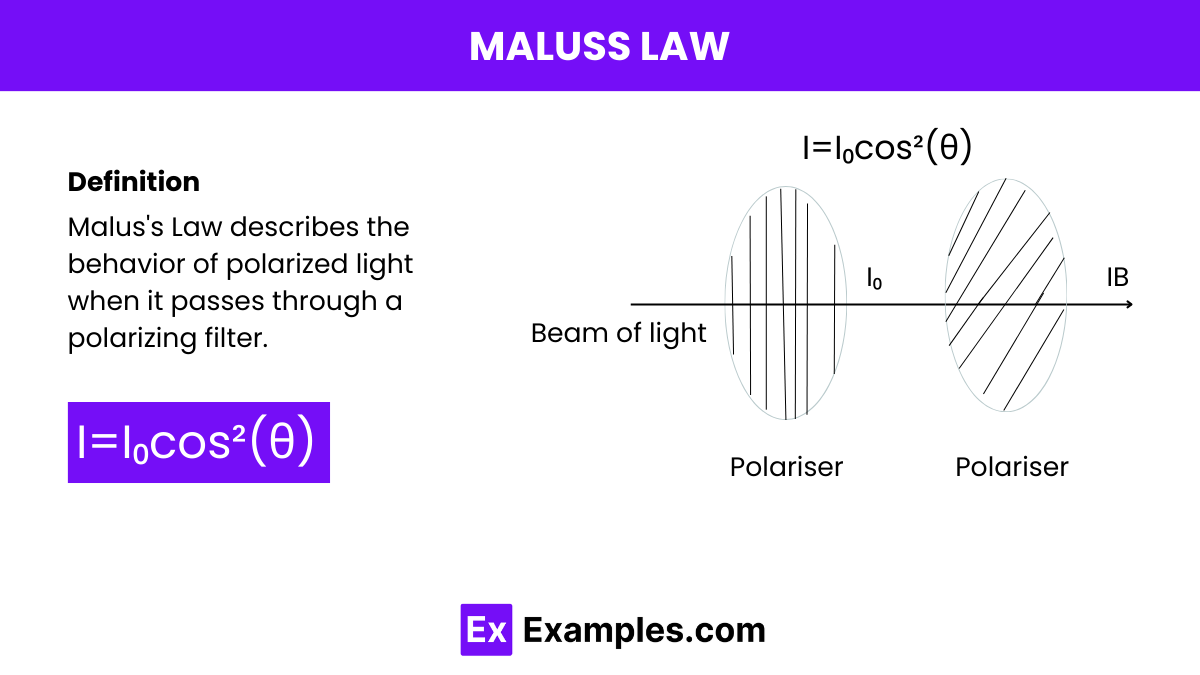
The formula for Malus’s Law, which describes how the intensity of polarized light changes as it passes through a polarizing filter, is given by:
Where:
𝐼 is the intensity of the light after passing through the filter, 𝐼₀ is the initial intensity of the polarized light before it reaches the filter,𝜃 is the angle between the polarization direction of the incoming light and the axis of the polarizing filter.
The derivation of Malus’s Law involves understanding the behavior of polarized light as it passes through a polarizing filter. Here’s a step-by-step explanation of how the law is derived:
Step 1: Understanding Polarized Light
Polarized light consists of waves that oscillate in a single plane. When light is initially polarized, it has an intensity 𝐼₀, and its electric field oscillates along a certain direction.
Step 2: Interaction with a Polarizing Filter
When this polarized light encounters a polarizing filter, the filter allows through only the component of the light’s electric field that aligns with its axis. If the polarization direction of the incoming light makes an angle 𝜃 with the polarizing axis of the filter, the component of the electric field that passes through the filter is 𝐸₀cos(𝜃), where𝐸₀ is the amplitude of the electric field of the incoming light.
Step 3: Calculating the Transmitted Intensity
The intensity of light, which is proportional to the square of the amplitude of the electric field, will then be modified by the square of the cosine of the angle 𝜃. Mathematically, the intensity 𝐼 of the light after passing through the filter is given by:
I=I₀cos²(θ)
Here, 𝐼₀ is the intensity of the incoming polarized light, and cos²(θ) reflects the reduction in intensity due to the alignment of the light with the filter.
Step 4: Law Formulation
This relationship I=I₀cos²(θ) , is known as Malus’s Law. It quantitatively describes how the intensity of polarized light diminishes as the angle between the light’s initial polarization direction and the filter’s axis increases.

Sunglasses
Polarized sunglasses use Malus’s Law to reduce glare from reflective surfaces like water or glass. The polarizing filters in the sunglasses are oriented to block horizontally polarized light, which is typically seen as glare, effectively reducing brightness and improving visual comfort.
Photography
Photographers use polarizing filters to enhance contrast and colors in their images. By adjusting the angle of the polarizing filter according to Malus’s Law, they can minimize reflections from surfaces such as water and glass, and darken the sky to bring out cloud details.
Optical Instruments
Instruments like polarimeters, which are used to measure the angle of rotation caused by optically active substances, employ Malus’s Law. By analyzing the intensity of light after it passes through a sample, scientists can determine the concentration of certain chemicals.
Liquid Crystal Displays (LCDs)
LCD screens utilize liquid crystal molecules that rotate polarized light. The intensity of light passing through these crystals and subsequently through a polarizing layer is governed by Malus’s Law, allowing precise control over pixel brightness.
Scientific Research
Malus’s Law is essential in experiments and studies involving light polarization, such as in the study of light scattering, stress analysis in materials, and even in quantum mechanics where polarization states are crucial.
Atmospheric Science
Researchers studying the Earth’s atmosphere use polarimeters equipped with polarizing filters to analyze scattered sunlight. By applying Malus’s Law, they can determine properties of atmospheric particles and pollutants, helping in climate studies and environmental monitoring.
Vision Science
In vision science, polarizing filters and the principles of Malus’s Law help in studying and testing the polarization sensitivity in various animals’ eyes. This sensitivity can be crucial for navigation, hunting, or avoidance of predators.
Quality Control in Manufacturing
In manufacturing processes, especially in the production of films, sheets, and glasses, polarized light and Malus’s Law are used to inspect material quality. This method helps detect imperfections and inconsistencies in material thickness or composition that are not visible to the naked eye.
Art Conservation and Analysis
Conservators use polarized light microscopy, applying Malus’s Law, to examine the layers and pigments in artworks. This technique allows them to understand the artwork’s structure without damaging it, aiding in preservation decisions and authenticity assessments.
Stress Analysis
In engineering, polarized light and Malus’s Law are used in photoelasticity to analyze stress distribution in materials. By observing the changes in light intensity through stressed transparent materials under polarized light, engineers can identify stress concentrations and potential failure points.
Malus’s Law originates from the work of Étienne-Louis Malus, a French physicist who discovered it in 1809 while studying the properties of polarized light.
Malus’s Law assumes that the light is perfectly polarized and the polarizer is ideal. In practical scenarios, deviations can occur due to partial polarization of light or imperfections in the polarizing filter.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What does Malus's Law describe?
The relationship between electric and magnetic fields
The intensity of light passing through a polarizer
The wavelength of light in different mediums
The frequency of electromagnetic waves
What is the formula for Malus's Law?
I = I₀ sin²θ
I = I₀ cos²θ
I = I₀ tan²θ
I = I₀ cosθ
If the angle between the light's initial polarization direction and the polarizer axis is 0°, what is the transmitted intensity?
I = 0
I = I₀
I = 0.5 I₀
I = 2 I₀
If the angle between the light's initial polarization direction and the polarizer axis is 90°, what is the transmitted intensity?
I = 0
I = I₀
I = 0.5 I₀
I = 2 I₀
What happens to the intensity of light if the polarizer is rotated by 60° with respect to the initial polarization direction?
I = I₀/2
I = I₀/4
I = 3I₀/4
I = I₀/8
If the initial intensity of light is 100 W/m² and the polarizer is at 30°, what is the transmitted intensity?
50 W/m²
75 W/m²
100 W/m²
25 W/m²
When unpolarized light passes through a polarizer, what happens to its intensity?
It doubles
It is reduced by half
It becomes zero
It remains the same
If the initial intensity of light is 200 W/m² and it passes through two polarizers at 60° to each other, what is the final intensity?
100 W/m²
25 W/m²
50 W/m²
75 W/m²
If light passes through three polarizers with angles 0°, 45°, and 90° respectively, what is the final intensity?
0.5 I₀
0.25 I₀
0
0.125 I₀
What is the intensity of light after passing through a polarizer if the initial light is already polarized and aligned with the polarizer's axis?
Zero
Half of the initial intensity
The same as the initial intensity
Twice the initial intensity
Before you leave, take our quick quiz to enhance your learning!

