Maxwell Boltzmann Formula

What is Maxwell Boltzmann Formula?

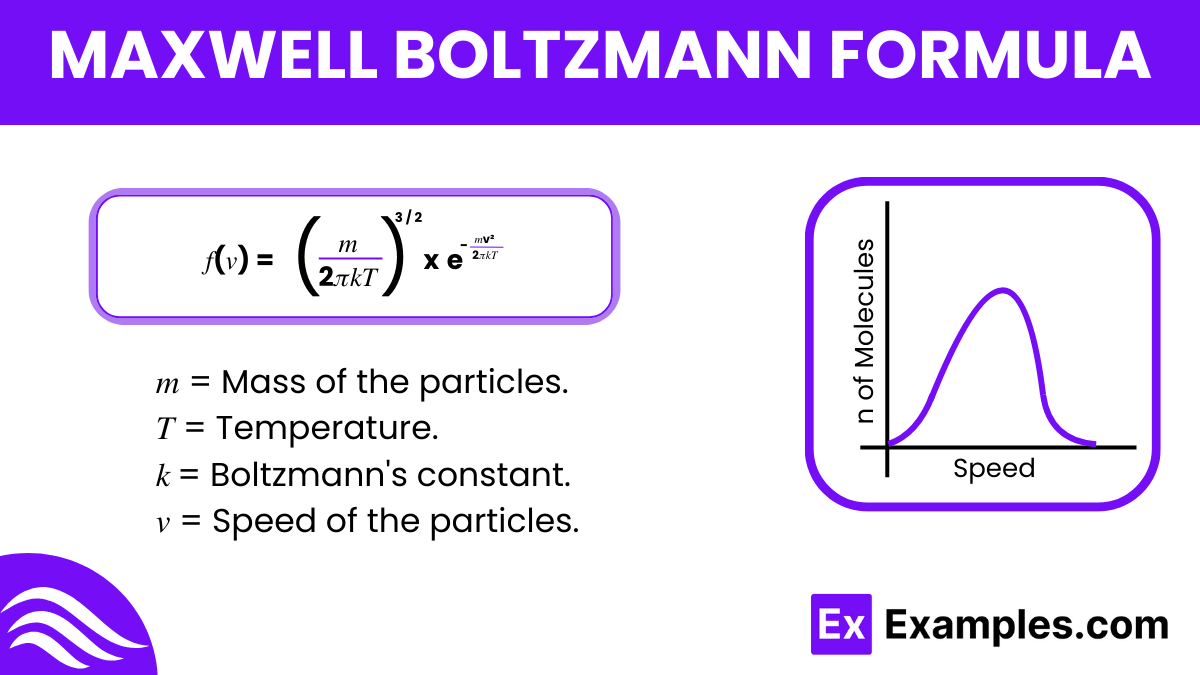
The Maxwell-Boltzmann formula, developed by James Clerk Maxwell and Ludwig Boltzmann in the 19th century, describes the speed distribution of particles in a gas at thermal equilibrium. This formula is pivotal in physics, especially in the study of statistical mechanics. It helps in understanding how particle speeds in a gas vary at a given temperature.

The formula is expressed as

𝑓(𝑣) = ( (𝑚 / 2𝜋𝑘𝑇)^ 3/ 2 ) x (𝑒 ^−𝑚𝑣² / 2𝑘𝑇)

• 𝑚 is the mass of the particles.
• 𝑇 is the temperature.
• 𝑘 is Boltzmann’s constant.
• 𝑣 is the speed of the particles.

This equation shows that most particles in a gas move at moderate speeds, with very few moving very quickly or very slowly, providing a statistical view of molecular motion in gases.

Usages of Maxwell Boltzmann Formula

• Predicting Gas Properties: It calculates properties like pressure and temperature of gases, crucial for understanding gas behavior in various conditions.
• Engineering Applications: Engineers use this formula to design and optimize systems involving gas flow, such as jet engines and exhaust systems.
• Chemical Reaction Rates: The formula helps in estimating the speeds of molecules which is vital for determining how fast chemical reactions occur.
• Astrophysics: It aids in analyzing the distribution of speeds of particles in stars and planetary atmospheres, offering insights into their thermal properties.
• Material Science: Understanding the diffusion of gases through materials, important for creating efficient filters and membranes.

Example Problems on Maxwell Boltzmann Formula

Problem 1: Calculating Particle Speed

Question: In a container of helium gas at 300 K, estimate the most probable speed of the helium atoms. Assume the mass of a helium atom is 4×10⁻²⁷ kg.

Solution:

The most probable speed 𝑣𝑝vp​ can be calculated using the formula: 𝑣𝑝 = √ 2𝑘𝑇 / 𝑚 Where:

𝑘=1.38×10⁻²³ J/K (Boltzmann constant),

𝑇=300 K,

𝑚=4×10⁻²⁷ kg.

Plugging in the values:

𝑣𝑝 = √( ( 2 × 1.38 × 10⁻²³ × 300 ) / ( 4 × 10⁻²⁷ ) ) ≈ 1370 m/s

Problem 2: Comparing Particle Speeds

Question: Compare the most probable speeds of hydrogen and oxygen molecules in a gas mixture at 400 K. Assume the mass of a hydrogen molecule (H₂) is 2 × 10⁻²⁷ kg and the mass of an oxygen molecule (O₂) is 32×10⁻²⁷ kg.

Solution: Calculate the most probable speed for each:

Hydrogen:

𝑣𝑝, H₂ = √ 2𝑘𝑇 / 𝑚H₂ = √ (( 2 × 1.38 × 10⁻²³ × 400) / (2×10⁻²⁷)) ≈ 1838 m/s

Oxygen:

𝑣𝑝, O₂ = √ 2𝑘𝑇 / 𝑚O₂ = √ ( (2×1.38×10⁻²³ × 400 ) / ( 32 × 10⁻²⁷ ) ) ≈ 459 m/s

Problem 3: Determining Kinetic Energy Distribution

Question: Calculate the fraction of nitrogen molecules (molecular mass 28×10⁻²⁷ kg) moving faster than 500 m/s at a temperature of 298 K.

Solution: First, calculate the fraction using the Maxwell-Boltzmann speed distribution function for speeds greater than 500 m/s. We use the cumulative distribution function (CDF):

Fraction=∫∞₅₀₀𝑓(𝑣) 𝑑𝑣

Where 𝑓(𝑣) is the Maxwell-Boltzmann distribution function. We simplify by using an integral table or computational tools because the integral calculation involves exponential functions:

Fraction ≈ 0.12

FAQs

What Does Maxwell-Boltzmann Show?

Maxwell-Boltzmann distribution illustrates how gas particles’ speeds vary at a specific temperature, predicting molecular motion in thermal equilibrium.

What is K in Boltzmann’s Formula?

In Boltzmann’s formula, 𝑘k represents the Boltzmann constant, 1.38×10⁻²³ J/K, linking temperature with energy.

What is the Formula for Maxwell Boltzmann Statistics?

The Maxwell-Boltzmann formula is 𝑓(𝑣) = ( (𝑚 / 2𝜋𝑘𝑇)^ 3/ 2 ) x (𝑒 ^−𝑚𝑣² / 2𝑘𝑇)​, defining particle speed distribution in gases.