Stefan-Boltzmann Law
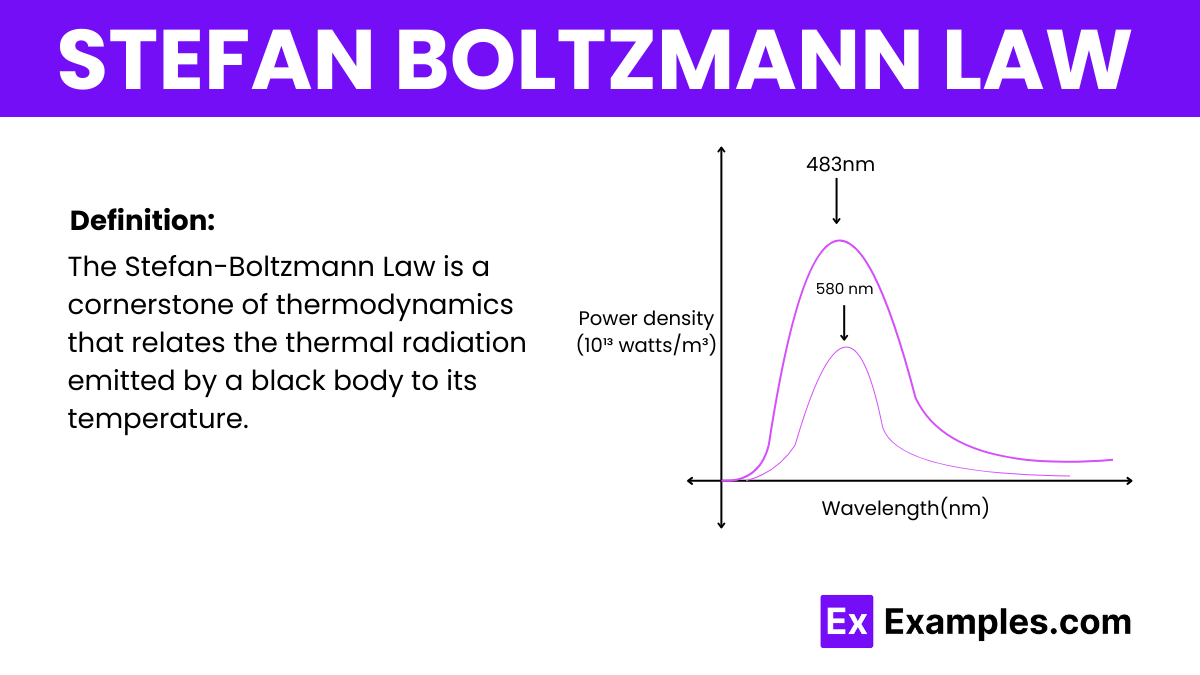
The Stefan-Boltzmann Law, often referred to as Stefan’s Law, is a crucial principle in the Laws of Thermodynamics and physics, detailing how the power radiated from a black body relates to its temperature. Specifically, this law articulates that the total energy emitted per unit surface area of a black body across all wavelengths per unit time (j*) is directly proportional to the fourth power of the black body’s temperature (T). This relationship is a cornerstone in the Laws of Physics, providing essential insights into the thermal behavior of objects across various scientific fields.
What Is Stefan Boltzmann Law?
Stefan Boltzmann Formula
The Stefan-Boltzmann formula is a fundamental equation in the field of thermodynamics and physics, quantifying the amount of energy a black body radiates based on its temperature. The formula is crucial for studies in various scientific areas, including physics, astronomy, and engineering, because it links thermal radiation to temperature using a simple yet powerful relationship.
The Stefan-Boltzmann formula is given by:
- j∗ is the total power per unit area emitted by a black body,
- σ is the Stefan-Boltzmann constant, approximately 5.67×10⁻⁸ W m⁻²K⁻⁴
- 𝑇 is the absolute temperature of the black body in kelvins.
Derivation of Stefan Boltzmann Law
To derive the Stefan-Boltzmann Law, we integrate Planck’s radiation formula over all wavelengths. The power radiated per unit area (𝐴) as a function of wavelength (𝜆) is given by:
𝑑𝑃/𝑑𝜆1/𝜆=2𝜋ℎ𝑐²/𝜆⁵ 1/𝑒^ℎ𝑐/𝜆𝑘𝑇−1
where:
-
- 𝑃 is the power radiated,
- 𝜆 is the wavelength of emitted radiation,
- ℎ is Planck’s constant,
- 𝑐 is the speed of light,
- 𝑘 is Boltzmann’s constant, and
- 𝑇 is the temperature.
After simplifying, the equation becomes:
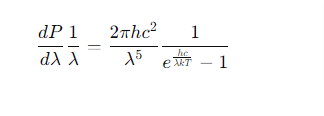
We then integrate this with respect to wavelength (𝜆) to find the total power:
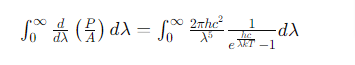
The power per unit area after separating the constants is:
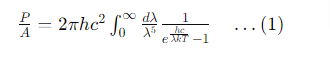
We solve this by substituting:
This substitution changes the integral into:
which yields:
Substituting back into equation (1) and simplifying, we obtain the Stefan-Boltzmann Law:
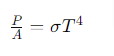
where:
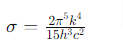
is the Stefan-Boltzmann constant. Thus, the total radiated power per unit area of a blackbody is proportional to the fourth power of its temperature.
Value of Stefan-Boltzmann Constant
Here’s the Stefan-Boltzmann constant presented in various unit systems:
| Unit System | Value of σ | Units |
|---|---|---|
| SI | 5.670367×10−85.670367×10−8 | W/(m²K⁴) |
| CGS | 5.6704×1055.6704×105 | erg/(cm² s¹ K⁴) |
| Thermochemistry | 11.7×10811.7×108 | cal/(cm² day K⁴) |
| U.S. Customary Units | 1.714×1091.714×109 | BTU/(ft² hr °R⁴) |
Uses of Stefan-Boltzmann Law
The Stefan-Boltzmann Law, a cornerstone in thermodynamics and astrophysics, has numerous applications across various fields. This law is crucial for understanding the phenomena involving thermal radiation.
-
-
- Earth’s Temperature Calculation: Climate scientists use the Stefan-Boltzmann law to estimate the Earth’s equilibrium temperature. By accounting for the Earth’s absorption and emission of solar and terrestrial radiation, researchers can model climate changes and understand global warming trends.
-
- Star Temperature Estimation: Astronomers apply this law to determine the surface temperatures of stars. By measuring the energy output from a star and knowing its distance, the temperature can be accurately inferred, which is essential for classifying stars and understanding stellar evolution.
-
- Radiative Energy of Celestial Bodies: This law helps calculate the radiative energy output of planets, stars, and other celestial bodies, aiding in the study of their composition and atmospheres.
-
- Thermal Management: In engineering, the Stefan-Boltzmann law is used to design systems that manage thermal energy effectively. This includes everything from electronic devices to large-scale industrial machinery, where controlling heat transfer is critical for efficiency and safety.
-
- Energy Efficiency Studies: Engineers use this law to improve the energy efficiency of buildings and other structures by analyzing heat transfer characteristics and the emissive properties of materials.
-
- Emissivity Measurement: The law is crucial for measuring the emissivity of materials. Emissivity is a material’s ability to emit energy as thermal radiation, which is vital for designing thermal insulation and for applications in aerospace and automotive industries.
-
- Thermography: In medical diagnostics, thermography techniques use the Stefan-Boltzmann law to detect and record the thermal patterns on the surface of the body. This method can help in early diagnosis of diseases like breast cancer or monitoring of inflammatory diseases.
-
Examples for Stefan Boltzmann Law
- Astronomers calculate the temperature of stars by measuring their emitted energy. For instance, the Sun’s temperature is approximately 5778 K, calculated based on its luminosity and radius.
- Earth’s Energy Budget:
- Scientists estimate Earth’s equilibrium temperature using solar radiation and Earth’s radiative emission. This calculation is vital for climate modeling and understanding global energy balance.
- Industrial Heat Management:
- Engineers design furnaces by calculating radiative heat transfer using the Stefan-Boltzmann law. This ensures the furnaces are efficient by minimizing thermal losses at high temperatures.
- Medical Imaging:
- Infrared thermography uses this law to diagnose diseases. By analyzing the infrared radiation from the body, doctors can detect issues like vascular disorders and muscle injuries.
- Material Testing:
- Material scientists determine the emissivity of materials. Observing radiation emitted by materials at controlled temperatures helps identify properties essential for thermal insulation and heat-resistant applications.
FAQ’S
What is the Stefan-Boltzmann law state?
The Stefan-Boltzmann law states that the total energy radiated per unit surface area of a black body is proportional to the fourth power of its temperature.
What is the Stefan-Boltzmann law deduce?
From thermodynamic principles, the Stefan-Boltzmann law deduces that radiation intensity increases dramatically with temperature, emphasizing the strong dependence of thermal radiation on temperature.
How do you use Stefan-Boltzmann law?
To apply the Stefan-Boltzmann law, multiply the Stefan-Boltzmann constant by the temperature to the fourth power, often used to calculate the radiative heat transfer of bodies.
Share :
