Parallelogram Law of Vector Addition

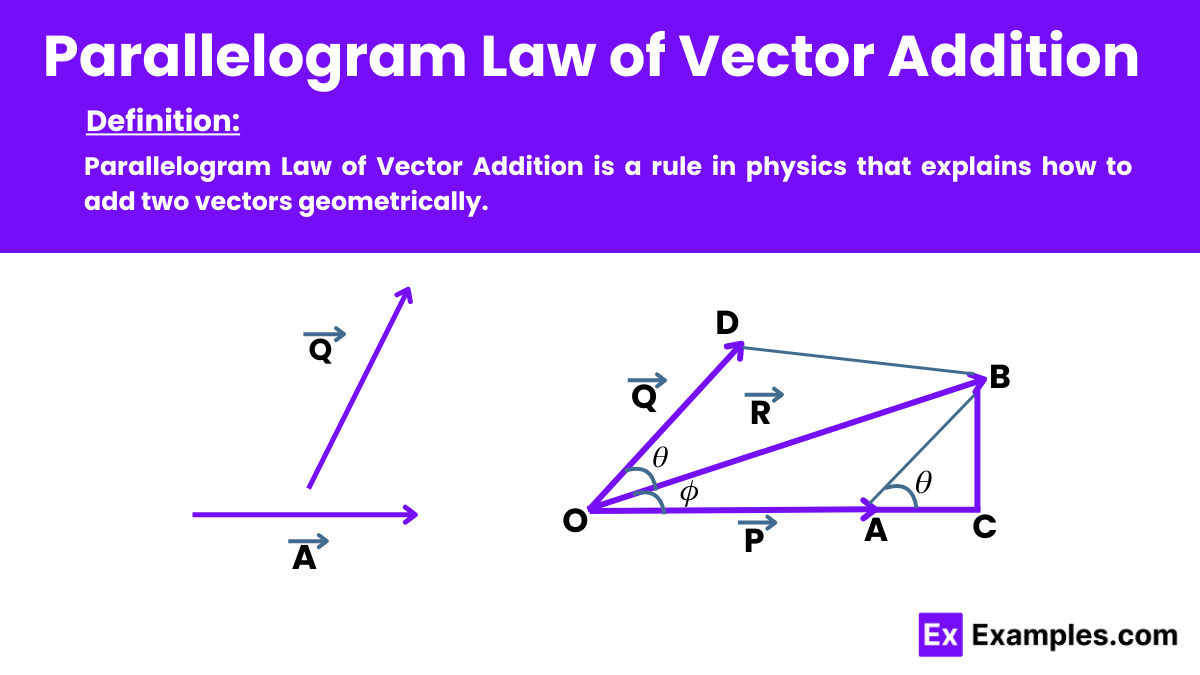
Parallelogram Law of Vector Addition is a rule in physics that explains how to add two vectors geometrically. According to this law of physics, if two vectors are represented as adjacent sides of a parallelogram, the diagonal that starts from the same point as the vectors represents their resultant. The magnitude and direction of this diagonal give the sum of the vectors. This law is fundamental in physics, as it helps in visually determining the resultant vector of two forces acting at an angle to each other.

What is Parallelogram Law of Vector Addition ?

Parallelogram Law of Addition

Parallelogram Law of Forces

The Parallelogram Law of Forces helps you find the resultant of two forces acting simultaneously on an object. According to this law, when two forces act on an object from the same point and at a certain angle to each other, you represent them as adjacent sides of a parallelogram. Consequently, the diagonal of the parallelogram, drawn from the same point, provides the magnitude and direction of the resultant force. By applying this law, you can effectively determine the combined impact of two distinct forces acting on an object. Providing a clear visual method for understanding vector addition in physics.

Parallelogram Law of Vector Addition Formula

The formula for the Parallelogram Law of Vector Addition involves finding the resultant of two vectors. 𝐴 and 𝐵, which form adjacent sides of a parallelogram. The magnitude of the resultant vector 𝑅 is:

where:

• 𝑅: Magnitude of the resultant vector
• P: Magnitude of vector P
• Q: Magnitude of vector Q
• 𝜃: Angle between vectors 𝐴 and 𝐵

The direction of the resultant vector can also be found using trigonometric relationships based on the magnitudes and the angle between the original vectors.

Parallelogram Law of Vector Addition Proof

Let vectors 𝑃 and 𝑄 represent two adjacent sides of a parallelogram. The diagonal 𝑅 represents the resultant vector.

2. Applying the Law: The parallelogram law states that the diagonal 𝑅 equals the sum of vectors 𝑃 and 𝑄: R=P+Q

3. Breaking Down the Geometry: Extend line DA to C, and draw BC perpendicular to OC. From the right-angled triangle △𝑂𝐶: 𝑂𝐵²=𝑂𝐶²+𝐵𝐶² Substitute 𝑂𝐶=𝑂𝐴+𝐴𝐶 to get: 𝑂𝐵²=(𝑂𝐴+𝐴𝐶)²+𝐵𝐶²

4. Analyzing the Angles: In triangle △𝐴𝐵𝐶:

• cos⁡𝜃=𝐴𝐶/𝐴𝐵⇒𝐴𝐶=𝐴𝐵cos⁡𝜃=𝑄cos⁡𝜃
• sin⁡𝜃=𝐵𝐶/𝐴𝐵⇒𝐵𝐶=𝐴𝐵sin⁡𝜃=𝑄sin⁡𝜃

5. Substituting and Simplifying: Substitute the values of 𝐴𝐶 and 𝐵𝐶 into the expression:

𝑅²=√(𝑃+𝑄cos⁡𝜃)²+(𝑄sin⁡𝜃)²

Expanding and simplifying further: 𝑅²=𝑃²+2𝑃𝑄cos⁡𝜃+𝑄²cos⁡²𝜃+𝑄²sin⁡²𝜃

Using the trigonometric identity cos⁡²𝜃+sin⁡²𝜃=1: 𝑅²=𝑃²+2𝑃𝑄cos⁡𝜃+𝑄²

6. Resultant Magnitude: Taking the square root gives the magnitude of the resultant vector: 𝑅=√𝑃²+𝑄²+2𝑃𝑄cos⁡𝜃​

7. Direction of Resultant Vector: To find the angle 𝜙 between 𝑅 and 𝑃,

we use: tan⁡𝜙=𝑄sin⁡𝜃/𝑃+𝑄cos⁡𝜃

Thus, the direction of 𝑅 is : 𝜙=tan⁡⁻¹(𝑄sin⁡𝜃/𝑃+𝑄cos⁡𝜃)

Special Cases of Parallelogram Law of Vector Addition

Important Points of Parallelogram Law of Vector Addition

Here are some important points about the Parallelogram Law of Vector Addition:

1. Geometric Interpretation: The law provides a graphical method to find the resultant of two vectors. If you draw the two vectors as adjacent sides of a parallelogram, the diagonal represents their sum.
2. Resultant Vector: The resultant vector is the diagonal starting from the same point as the vectors. Its magnitude and direction are determined by the relative magnitudes and directions of the original vectors.
3. Applicability: The law applies to any two vectors, regardless of their magnitudes and the angle between them, allowing you to compute the resultant vector in many scenarios.
4. Magnitude Calculation: You can calculate the magnitude of the resultant vector using the formula 𝑅=√𝐴²+𝐵²+2𝐴𝐵cos⁡𝜃​, where 𝜃 is the angle between the two vectors.
5. Direction of Resultant: The direction of the resultant vector can be calculated using trigonometric relationships, providing both the magnitude and direction.
6. Vector Properties: The law maintains vector properties such as commutativity. Meaning you get the same resultant vector regardless of the order of the two vectors.
7. Practical Applications: Engineers and physicists use this law frequently to analyze forces, velocities, and other vector quantities in physics and engineering problems.

Uses of Parallelogram Law of Vector Addition

1. Engineering Mechanics: Engineers often rely on the parallelogram law to analyze and resolve forces in structures. Thereby ensuring stability and safety in bridges, buildings, and machines.
2. Physics: Physicists use this law to find the resultant of different physical quantities like displacement, velocity, and acceleration, simplifying complex motion problems.
3. Navigation: Navigators use the law to determine the actual path and speed of a ship or aircraft when subjected to multiple forces such as wind and currents.
4. Robotics: In robotics, this law helps in calculating the resultant motion when different actuators apply varying forces on a robotic arm, making control and movement more precise.
5. Computer Graphics: In computer graphics, designers use the law to calculate the resultant direction and magnitude of forces affecting an object. Allowing for more realistic motion simulations.
6. Astronomy: Astronomers use the law to understand the combined gravitational influences on celestial bodies. Improving predictions of planetary orbits and space travel trajectories.

Examples for Parallelogram Law of Vector Addition

1. Bridge Design: Engineers use the parallelogram law to calculate the resultant forces acting on a bridge. This simplifies the design process by ensuring the structure withstands multiple loads effectively.
2. Navigation: Pilots apply the law to find the actual course and speed of an aircraft. They consider the effects of wind and other factors. Allowing for precise navigation.
3. Physics Problems: Physicists employ the parallelogram law to resolve two-dimensional force problems. This helps in analyzing the resultant forces acting on an object in motion.
4. Robot Movement: In robotics, developers rely on this law to determine the direction and speed of a robot. It helps them understand the combined influence of different actuators.
5. Vehicle Motion: Automotive engineers use this law to calculate the resultant vector of forces acting on a vehicle. It helps optimize performance by analyzing factors like engine power and road friction.

FAQ’S

What is the parallelogram law of vector subtraction?

This method involves reversing the direction of one vector and then applying the parallelogram law to find the resultant. Effectively subtracting one vector from another.

What are the two types of vector addition?

The two types of vector addition include the head-to-tail method and the parallelogram method, which allow the graphical or analytical combination of two or more vectors.

How to find resultant force?

You can find the resultant force by summing all individual forces as vectors. Considering both magnitude and direction to find their combined effect.